ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
МАТЕМАТИКА
Группа 21М571в
Студент
С.И. Сидоров
МОСКВА 2022
-
Выполнить деление комплексных чисел
1.1
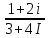 =
=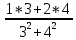 +
+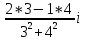 =
=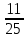 +
+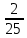 i=0,44+0,08i
i=0,44+0,08i1.2
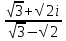 =
=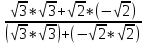 =
=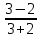 +i
+i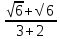 =
=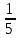 +
+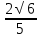 i=0,2+0,98i
i=0,2+0,98i2. Вычислить пределы последовательностей
2.1
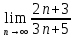 =
=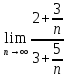 =
=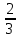
2.2
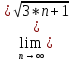 -
- 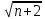 )=
)=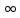
Домножим и разделим на
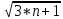 -
- 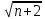 )
)=
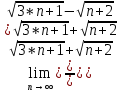 =
= 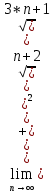 )=
)=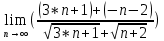 =
=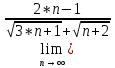 )=разделим числитель и знаменатель на
)=разделим числитель и знаменатель на
sgrt(n)
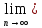 (
(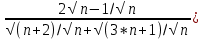 =
=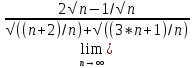 )=
)=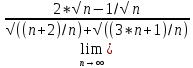 )=
)=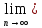 (
(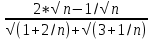 )= /сделаем замену a=
)= /сделаем замену a=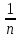 /
/ 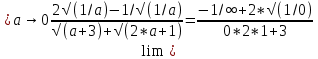 )=
)=
3. Используя признаки Даламбера и Коши исследовать сходимость рядов
3.1
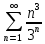
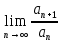 =
=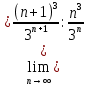 )=
)=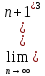 =
=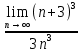 =
= 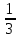
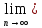 (
(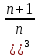 =
= 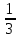
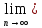 (1+
(1+ 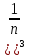 =
= 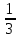
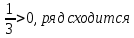
3.2
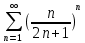
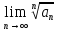 =
=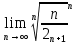 =
=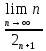 =
=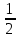
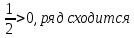
4. Найти производные сложных функций
4.1 Y=
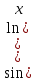
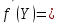
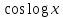
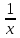
4.2 y=
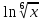
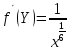 *
*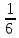
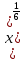 -1) =
-1) =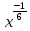 *
* 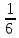 *
*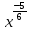 =
= 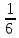
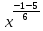 =
=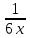
5. Вычислить неопределенный интеграл
5.1
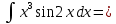 /Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:/
/Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:/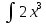 sin(x) cos(x) dx=2
sin(x) cos(x) dx=2 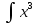 sin(x) cos(x)dx /интегрируем по частям
sin(x) cos(x)dx /интегрируем по частям 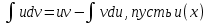 =
= 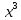 и dv(x)=3
и dv(x)=3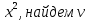 (x):
(x):Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции
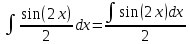 , пусть U=2x, тогда du=2dx ,подставим
, пусть U=2x, тогда du=2dx ,подставим 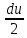 :
: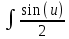 du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: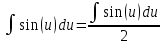
Интеграл от синуса – минус косинус:
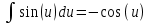 , результат -
, результат -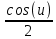 , если заменить u в
, если заменить u в 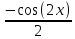 , получим
, получим 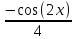
Интегрируем по частям:
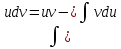 , пусть u(x)=-
, пусть u(x)=- 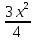
, dv(x)= -
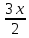
Пусть U=2x, тогда du=2dx, подставим
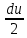 :
: 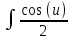 du
duИнтеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
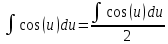
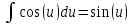 , результат
, результат 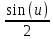 , заменим u в
, заменим u в 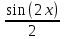
Интегрируем по частям:
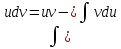 , пусть u(x)= -
, пусть u(x)= - 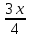 и пусть dv(x)=sin(2x)
и пусть dv(x)=sin(2x)Затем du(x)=-
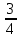
Пусть u=2x, тогда пусть du=2dx и подставим
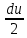
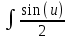 du
duИнтеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
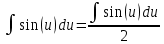
Интеграл от синуса есть минус косинус:
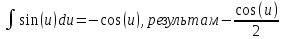 , если заменить u в
, если заменить u в 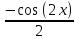 , учитывая что Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
, учитывая что Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: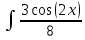 dx=
dx= 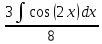 , пусть u=2x, тогда du=2dx, подставим
, пусть u=2x, тогда du=2dx, подставим 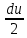
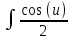 du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: 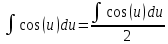
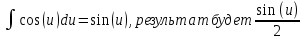 , если u заменить
, если u заменить 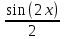 , получится
, получится 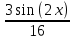
Результат будет:
-
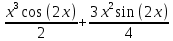 +
+ 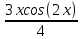
-
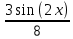 , добавляем постоянную интегрирования:
, добавляем постоянную интегрирования:-
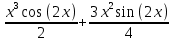 +
+ 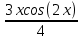 -
- 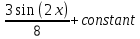
5.2
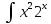 dx=-
dx=- 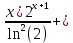
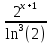 +
+ 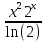 +C
+C/ Интегрируем по частям: :
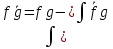
f=
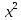 , g=
, g=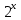
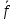 =2x,
=2x, 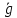 =
=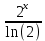 /
/=
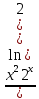 -
- 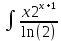 dx
dx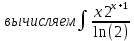 = / применяем линейность/=
= / применяем линейность/= 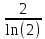
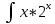 dx, вычисляем:
dx, вычисляем: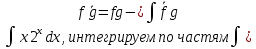
f=x,
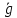 =
=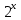
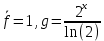
=
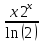 -
- 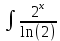 dx, вычисляем
dx, вычисляем 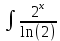 dx=
dx= 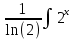 dx
dxВычисляем
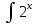 dx /
dx / 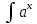 dx =
dx =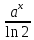 , при a=2 / =
, при a=2 / =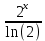
Подставляем вычисленные интегралы:
