Файл: Тесты к экзамену по учебной дисциплине " Математика ".docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕСТЫ К ЭКЗАМЕНУ
по учебной дисциплине
"Математика "
ЧИСЛОВЫЕ РЯДЫ
Составитель ст.пр. Обручева Т.С.
Санкт-Петербург
2013
| № | Вопросы | Варианты ответов | |
| | ЧИСЛОВЫЕ РЯДЫ | | |
| | КАТЕГОРИЯ 1 | | |
| | Ряд сходится, если ( 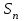 — его — его 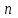 -я частичная сумма) -я частичная сумма) | 1. 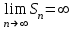 2. 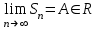 3. 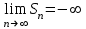 4. 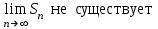 | |
| | Что называется остатком числового ряда  ? ? | 1. 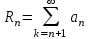 2. 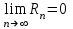 3. 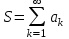 4.  | |
| | Что такое 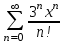 -я частичная -я частичная сумма ряда  ? ? | 1. 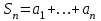 2. 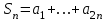 3. 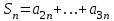 4. 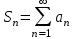 | |
| | Указать общий член ряда 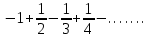 | 1. 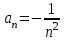 2. 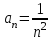 3.  4. 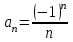 | |
| | Указать необходимый признак сходимости. |
| |
| | Если ряд  сходится, то ряд сходится, то ряд 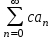 , где , где 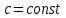 , , |
| |
| | Какой из указанных числовых рядов сходится? | 1. 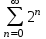 2. 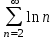 3. 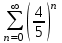 4. 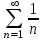 | |
| | Указать гармонический ряд | 1. 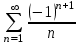 2. 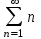 3. 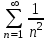 4. 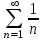 | |
| | В чем заключается достаточный признак расходимости? | 1. 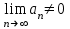 2.  3. 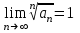 4. 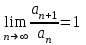 | |
| | Указать, когда ряд Дирихле 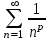 сходится сходится | 1. 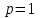 2. 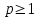 3. 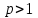 4. 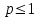 | |
| | Числовые ряды  и и 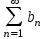 одновременно сходятся или расходятся, если одновременно сходятся или расходятся, если | 1. 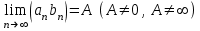 2. 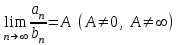 3. 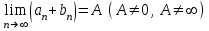 4. 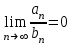 | |
| | Какой числовой ряд проще исследовать по теореме сравнения в предельной форме (сравнить с рядом 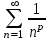 ) ? ) ? | 1. 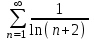 2. 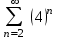 3. 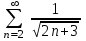 4. 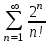 | |
| | С каким рядом надо сравнивать ряд 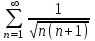 , чтобы установить его сходимость (расходимость)? , чтобы установить его сходимость (расходимость)? | 1. 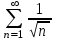 2. 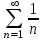 3. 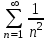 4. 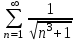 | |
| | Если для ряда  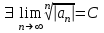 , то , то |
| |
| | Каким признаком лучше всего исследовать ряд 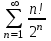 |
| |
| | C помощью какого из признаков можно исследовать данный ряд 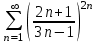 на сходимость | 1.интегральный признак Коши 2.радикальный признак Коши 3.признак сравнения 4.признак сравнения в предельной форме | |
| | Чему равен предел при исследовании ряда  по признаку Даламбера? |
| |
| | Чему равен предел при исследовании ряда 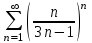 по признаку Коши (радикальному)? | 1. 0 2. 1 3. 3 4. 1/3 | |
| | Какие условия являются достаточными для сходимости знакочередующегося ряда 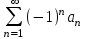 (признак Лейбница)? |
| |
| | Знакопеременный ряд  (ряд А) называется абсолютно сходящимся (ряд А) называется абсолютно сходящимся | 1.Если ряд  сходится сходится2.Если ряд А сходится, а ряд 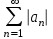 расходится расходится3.Если ряд А сходится, то  4.Если ряд 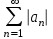 сходится сходится | |
| | Почему ряд 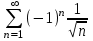 является условно сходящимся? | 1.Т.к. расходится ряд 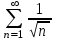 2.Т.к. сходится ряд 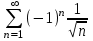 , а ряд , а ряд 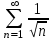 расходится расходится3.Т.к. сходится ряд 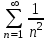 4.Т.к.  | |
| | Почему ряд 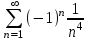 является абсолютно сходящимся? | 1.Т.к. 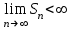 2.Т.к. сходится ряд 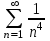 3.Т.к. 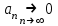 4.Т.к. 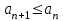 | |
| | Указать правильное окончание теоремы Лейбница: Ряд 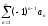 сходится, если сходится, если |
| |
| | Какой числовой ряд можно исследовать по признаку Лейбница | 1. 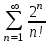 2. 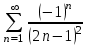 3. 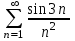 4. 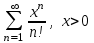 | |
| | Ряд 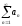 (ряд А) называется условно сходящимся (ряд А) называется условно сходящимся | 1.Если ряд  сходится сходится2.Если ряд А сходится, а ряд 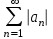 расходится расходится3.Если ряд А сходится, то  4.Если ряд 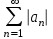 сходится сходится | |
| | КАТЕГОРИЯ 2 | | |
| | Ряд  сходится тогда и только тогда, когда сходится тогда и только тогда, когда | 1. Последовательность его частичных сумм ограничена 2. 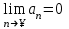 3. Последовательность его частичных сумм сходится 4. Последовательность его частичных сумм сходится к нулю | |
| | Для какого из данных рядов выполняется необходимый признак сходимости? | 1. 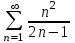 2. 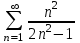 3.  4. 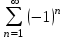 | |
| | Положительный ряд  сходится тогда и только тогда, когда сходится тогда и только тогда, когда | 1. 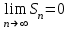 ( (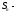 частичная сумма ряда) частичная сумма ряда)2.  3. 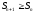 4.  5. 5.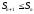 | |
| | Указать общий член ряда 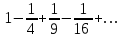 | 1. 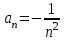 2. 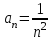 3.  4. 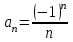 | |
| | Если ряды  и и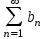 сходятся, то, сходятся ли ряды сходятся, то, сходятся ли ряды 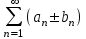 ? ? | 1.сходятся 2.невозможно определить 3. ряд 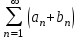 расходится, а ряд расходится, а ряд 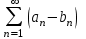 сходится сходится4.расходятся | |
| | Указать геометрический ряд | 1. 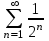 2.. 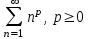 3. 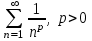 4. 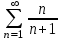 | |
| | Какой из указанных числовых рядов сходится? | 1. 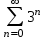 2. 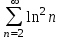 3. 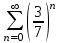 4. 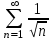 | |
| | Указать ряд Дирихле | 1. 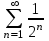 2. 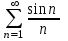 3. 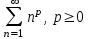 4. 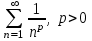 | |
| | Сформулируйте достаточный признак расходимости? | 1. 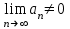 2.  3. 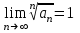 4. 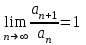 | |
| | Какое из приведенных утверждений верно? |
| |
| | Члены рядов А:  и В: и В: 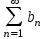 удовлетворяют условию: удовлетворяют условию: 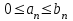 , тогда , тогда |
| |
| | Для положительных рядов А:  и В: и В: 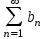 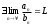 , тогда , тогда |
| |
| | Какой числовой ряд проще исследовать по теореме сравнения в предельной форме (сравнить с рядом 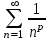 ) ? ) ? | 1. 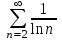 2. 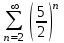 3. 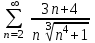 4. 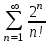 | |
| | Если для ряда  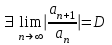 , то , то |
| |
| | Какой ряд можно исследовать по признаку Даламбера? | 1. 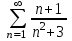 2. 2.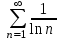 3. 3. 4. 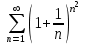 | |
| | Каким признаком лучше всего исследовать ряд  |
| |
| | C помощью какого из признаков можно исследовать данный ряд 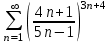 на сходимость | 1.интегральный признак Коши 2.радикальный признак Коши 3.признак сравнения 4.признак сравнения в предельной форме | |
| | Какой ряд целесообразно исследовать по радикальному признаку Коши? | 1.  2.  3. 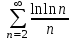 4. 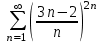 | |
| | Какой ряд целесообразно исследовать по интегральному признаку Коши? | 1. 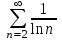 2.  3. 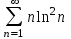 4. 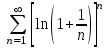 | |
| | C помощью какого из признаков можно исследовать данный ряд  на сходимость | 1.интегральный признак Коши 2.радикальный признак Коши 3.признак сравнения 4.признак сравнения в предельной форме | |
| | С помощью интегрального признака Коши установить, какие из приведенных ниже рядов сходятся 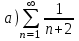 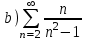 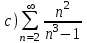 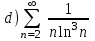 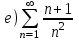 | | |
| | Сформулируйте признак Лейбница: Знакочередующийся ряд 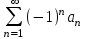 сходится, если сходится, если |
| |
| | Указать достаточный признак сходимости знакопеременного числового ряда  (ряда А) (ряда А) | 1.Если ряд  сходится, то сходится ряд А сходится, то сходится ряд А2.Ряд А сходится, а ряд 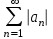 расходится расходится3.Если ряд А сходится, то  4.Если ряд 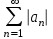 сходится, то ряд А сходится абсолютно сходится, то ряд А сходится абсолютно | |
| | Установить, какие из приведенных ниже рядов сходятся абсолютно 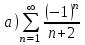 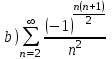 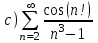 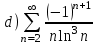 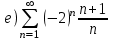 | 1. 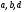 2. 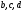 3. 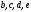 4. 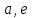 | |
| | Почему ряд 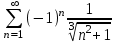 является условно сходящимся? | 1.Т.к. расходится ряд 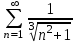 2.Т.к. сходится ряд 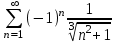 , а ряд , а ряд 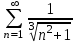 расходится расходится3.Т.к. сходится ряд 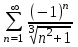 4.Т.к. 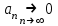 | |
Составитель
ст.препод. Обручева Т.С.
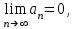 то ряд сходится.
то ряд сходится. то ряд сходится.
то ряд сходится.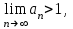 то ряд сходится.
то ряд сходится.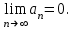
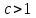
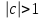
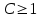 ряд сходится
ряд сходится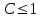 ряд расходится
ряд расходится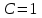 ряд сходится
ряд сходится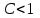 ряд абсолютно сходится
ряд абсолютно сходится 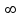
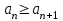
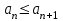
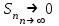 ,
, 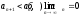
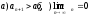
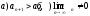
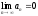
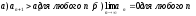
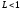
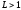
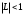 , А сходится, а В расходится
, А сходится, а В расходится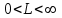
 ряд сходится
ряд сходится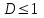 ряд расходится
ряд расходится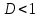 ряд абсолютно сходится
ряд абсолютно сходится 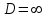 ряд сходится
ряд сходится