Файл: Курс лекций по дисциплине Цифровая схемотехника для специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 99
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 3
Преобразовать логическую функцию
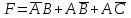
-
по формуле 11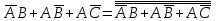
-
по формуле 14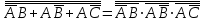
-
по формуле 15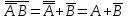
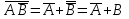
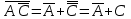
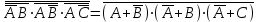
4.
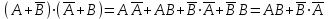
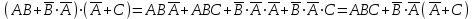
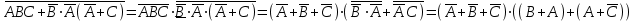 А+А=А
А+А=А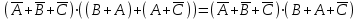
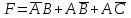 =
=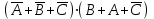
Принцип двойственности
Представленные законы (пары: (1) и (2), (3) и (4), (6) и (7), (9) и (10), (14) и (15), (19)# и (20), (21) и (22)) показывают, что между формулами, записанными слева и справа, существует вполне определенная зависимость. Если в любой формуле дизъюнкцию заменить конъюнкцией, конъюнкцию заменить дизъюнкцией, 0 заменить 1,1 заменить 0, а отрицание сохранить без изменения, то формула с нечетным номером (например, (9) перейдет в формулу с четким номером (10), и наоборот). Значит, с помощью указанных замен можно из одних равносильностей получить другие. Эта закономерность называется законом или принципом двойственности. Этот закон справедлив вообще для всех формул алгебры логики. Дело в том, что приведенных равносильностей вполне достаточно, чтобы с их помощью доказать любую другую равносильность. Поэтому установленная закономерность сохраняется и по отношению к любым другим равносильностям, если только соответствующие формулы не содержат импликацию. В связи с этим говорят, что операция конъюнкции двойственна операции дизъюнкции и наоборот, а формулы F1и F2называют двойственными, если одна получается из другой, как указано выше, заменой каждой операции на двойственную операцию.
Иллюстрацией сказанного является следующий пример.
Пример. Дана формула
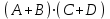 . Получить двойственную ей формулу.
. Получить двойственную ей формулу.Решение.
Преобразуем исходную формулу в равносильную.
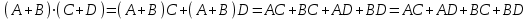
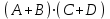 =
=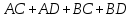
Составим теперь двойственную равносильность
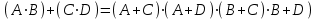
Эту равносильность можно доказать с помощью формулы (10).
Обобщая вышеприведенное правило получения двойственной формулы, в математической логике доказано, что если есть некоторая формула F(A,B,...,Z) и к ней двойственна логическая формула Ф(А,В,...Z) то они удовлетворяют тождествам
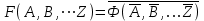 или
или 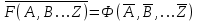 .
.Эти соотношения используют при преобразовании логических формуя и называют правилам отрицания, которое дополняет следствия алгебры логики.
Справедлив также принцип двойственности; Если две логические формулы F1(A,B,...,Z) и F2(A,B,...,Z) равносильны, то сеть
F1(A,B,...,Z) = F2(A,B,...,Z) и каждая из них имеет двойственную формулу Ф1(A,B,...,Z) и Ф2(A,B,...,Z), то равносильны и двойственные формулы
F1(A,B,...,Z) = F2(A,B,...,Z)
Тема 1.6 Переключательные функции
-
Переключательные функции
В логике не требуется знания абсолютного значения величины, поэтому физическая величина, подвергаемая логическим преобразованиям, называется переменной, или аргументом, и представляется ее положительная (Н) или менее положительная (L). Этим Значениям, называемым логическими уровнями, условно приравнивая значения 1 и 0, или наоборот 0 и 1, в зависимости от го соглашения.
Логические переменные могут подвергаться различным преобразованиям с использованием логических элементов. Такие преобразования описываются с помощью переключательных функций в которых используются различные буквы латинского алфавита: А, В, С, D, X, Y, x1, x2, хз и т.д.
Функция от входных переменных называется переключательной если она так же, как ее аргументы, принимает два значения: лог ческой единице (лог. 1) или логического нуля (лог. 0).
-
Основные базисы.
Одна из основных задач синтеза заключается в выборе типов элементов, на которых будут реализовываться заданные функции. Поэтому необходимо определить минимальный набор логических элементов (базис), образующих функционально полную систему элементов.
Базис — это функционально полный набор элементов, с помощью которого можно реализовать сколь угодно сложную переключательную функцию. Их может быть несколько. Базис из логических элементов И, ИЛИ, НЕ называется основным.
Пример:
Представить логическую функцию в базисе И-НЕ
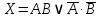 =
= 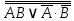 =
= 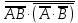 .
.Задания для самостоятельной работы
Представить заданные логические функции в заданном базисе
| Номер | Логические функции | Базис |
| 1 | 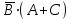 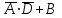 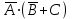 | И-НЕ |
| 2 | 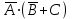 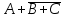 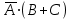 | И-НЕ |
| 3 | , , ; | И-НЕ |
| 4 | , , ; | ИЛИ-НЕ |
| 5 | , , ; | ИЛИ-НЕ |
| 6 | , , . | ИЛИ-НЕ |
Тема 1.7 Минимизация переключательных функций
-
Совершенные нормальные формы
С помощью эквивалентных преобразований логической функции можно получить различные формы ее представления. Одной из основных задач по преобразованию логических формул является получение равносильных формул в. так называемой, нормальной форме, и установления типа заданной формулы алгебры высказываний. Формула имеет нормальную форму, если в пси путем равносильных замен устранены операции эквиваленции, импликации, исключающей дизъюнкции, двойного отрицания, и при этом знаки отрицания находятся только при переменных. Таким образом, формула имеет нормальную форму, если она записана с помощью конъюнкции и дизъюнкции, действующих на совокупность переменных, и отрицания, действующего на отдельные переменные. Такие нормальные формулы называются дизъюнктивно-нормальную и конъюнктивно-нормальную формы.
Они являются наиболее удобными для определения тождественной истинности и тождественной ложности формул.
Для более корректного введения понятий дизъюнктивно-нормальную и конъюнктивно-нормальную формы, дадим определение основной конъюнкции и основной дизъюнкции.
Основная (элементарная) конъюнкция - это конъюнкция основных высказываний или их отрицаний. Например,
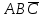
Основная (элементарная) дизъюнкция - это дизъюнкция основных высказываний иди их отрицаний. Например,
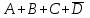 .
.Основная конъюнкция и дизъюнкция характеризуются рангом (порядком), который определяется количеством логических переменных в конъюнкции и дизъюнкции. С помощью основной конъюнкции и основной дизъюнкции можно определить дизъюнктивно-нормальную и конъюнктивно-нормальную формы.
Конъюнктивно-нормальной формой (КНФ)данной формулы называется формула, равносильная данной, и представленная в виде конъюнкции основных дизъюнкций. Например,
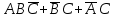 .
.Дизъюнктивно-нормальной формой (ДНФ)данной формулы называется формула, равносильная данной, и прсдставимая в виде дизъюнкций основных
конъюнкций. Например, АВС+ ВС + С + АС.
Алгоритм получения нормальной формы.
Каждая логическая формула может быть представлена в форме КНФ или ДНФ. Не существует ДНФ только для логической константы 0, а также не существует КНФ для логической константы 1. Для получения дизъюнктивно-нормальной и конъюнктивно-нормальной форм используются законы инфолюции и де Моргана, а также первый и второй дистрибутивные законы.
Для представления логической формулы в форме КНФ (ДНФ) необходимо:
-
С помощью законов инфолюции представить формулу в базисе - {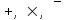 }
} -
С помощью законов де Моргана исключить отрицание над логическими операциями, а по закону двойного отрицания удалить двойные знаки отрицания. -
С помощью второго (первого) дистрибутивного закона удалить все суммы произведений (все произведения сумм) и произвести поглощение.
Рассмотрим несколько примеров преобразования логических формул и получения их нормальных форм.
Пример 1.
Привести к конъюнктивно-нормальной форме логическую формулу.
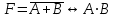
Решение.
В соответствии с предложенной методикой, получим эквивалентную ей формулу в базисе {
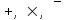 }. Для этого с помощью законов инфолюции исключим операцию эквиваленции, и используя закон двойного отрицания и закона де Моргана, получим
}. Для этого с помощью законов инфолюции исключим операцию эквиваленции, и используя закон двойного отрицания и закона де Моргана, получим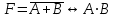 =
=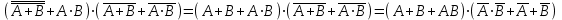
Пример 2.
Привести к ДНФ логическую формулу:
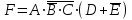
Решение
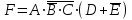 =
=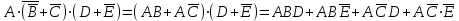
Пример 3.
Привести к нормальной форме и установить тип следующей формулы алгебры высказываний.
F=
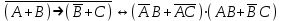
Решение
-
Исключить операцию эквиваленнции -
Исключить операцию импликации -
Исключить общие отрицания и раскрыть скобки, выполнить преобразования.
F=