Файл: Курс лекций по дисциплине Цифровая схемотехника для специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 133
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Непозиционные системы счисления
Все непозиционные системы счисления задаются перечислением изображаемых в них значений (или таблицей). Классическим примером непозиционной системы счисления является, так называемая, римская система счисления, в которой числа изображаются буквами латинского алфавита.
Так буква (символ) I всегда обозначает 1,
V всегда обозначает 5,
X всегда обозначает 10,
L всегда обозначает 50,
С всегда обозначает 100
D всегда обозначает 500,
М всегда обозначает 1000 и т.д.
Например, число 1678 запишется в римской системе счисления в виде MDCLXXVIII Из этого примера видно, что значения написанных рядом букв при изображении числа складываются. Для уменьшения числа требуемых символов, в римской системе счисления было введены дополнительные правила. Размещение меньшего числа справа от большего числа означает прибавление его к большему числу. Так VI - означает 6, XI - 11, LX - 60, а размещение меньшего числа слева от большего числа означает вычитание. Например, IV -означает 4, IX - 9, XL – 40. Число 247 запишется в виде –CCXLVII
Для записи больших чисел в непозиционных системах счисления надо либо записывать длинные строки из повторяющихся символов, либо увеличивать набор этих символов. Это и явилось общим недостатком всех непозиционных систем счисления. Поэтому для записи больших чисел в римской системе счисления, чтобы не вводить новых символов были введены дополнительные обозначения: над символами основного набора ставилась черточка, которая обозначала, что данный символ (число) надо умножить на 1000. Не такие приемы все равно не решали проблемы записи очень больших чисел, с которыми приходится иметь дело в повседневной жизни.
Самая простая непозиционная система счисления, имеющая наименьшее число символов — аддитивная система, в которой используется только одни символ – I. В ней единице соответствует I, 2 - II, 3 - III, 4 – IIII. И вообще, величина числа равна количеству одинаковых знаков его представления. Так как в этой системе используется только одна цифра - I, то иногда такую систему счисления называют единичной или палочной.
В непозиционных системах счисления количественные значения цифр не меняется при изменении их положения в последовательности цифр представляющей число
. В непозиционных системах счисления действия над числами связаны с большими трудностями и не имеют строгих правил, и в этих системах нельзя выражать отрицательные и дробные числа. В силу указанных недостатков, непозиционные системы счисления имеют ограниченное применение. В основном их используют для обозначения каких-либо натуральных чисел - как правило, для наименования дат, веков, годов, томов, глав и т.д.
Ранее использовались и другие непозиционные системы счисления. Так известны древнеегипетская и вавилонская непозиционные системы счисления. У древних славян использовалась, так называемая, алфавитная системы счисления, в которой в качестве цифр применялись буквы древнерусского алфавита,
Позиционные системы счисления
Большее распространение получили позиционные системы счисления, которые являются более совершенными по отношению к непозиционным системам счисления.
Позиционной системой счисления называется система представления чисел, в которой количественное значение каждой цифры, входящей в запись числа, зависит от места, то есть позиции, в ряду цифр, изображающих число.
В каждой позиционной системе счисления используется определенный набор символов (их договорились называть цифрами), последовательная запись которых изображает число.
Совокупность этих цифр используемых в позиционной системе счисления для записи чисел, называется алфавитом системы счисления или базой (базовые цифры).
Существуют различные позиционные системы счисления. Возможно бесчисленное множество позиционных систем, так как за основание можно принять любое число, образовав новую систему счисления. С теоретической точки зрения, основанием системы счисления может быть любое ненулевое число (в том числе отрицательные и даже комплексные). Наиболее часто используются системы счисления с натуральным основанием, более редко отрицательные целые и дробные основания. В теоретическом отношении все системы счисления равноправны. Лишь на практике отдельным системам отдастся предпочтение для тех или иных применений. Во всех системах счисления по одним и тем же правилам выполняются арифметические операции, справедливы одни и те же законы для этих операций.
Количество символов в алфавит системы счисления при натуральном основании соответствует основанию системы счисления.
Основание показывает, во сколько раз изменяется количественное значение каждой цифры при перемещении на соседнюю позицию, и какое число различных цифр входит в алфавит.
Позиция символа в изображении числа называется разрядом.
В позиционных системах различают понятие базиса системы счисления.
Базисом системы счисления называют последовательность чисел, каждое из которых показывает, во сколько раз меняется значение цифры в зависимости от се месторасположения (позиции) или "вес" каждого разряда.
Название системы счисления с натуральным основанием соответствует ее основанию, которое задастся в десятичной системе счисления (например, десятичная, двоичная, восьмеричной и т.д.), В математике и в обычной повседневной практике, чаще всего используется десятичная система счисления, в которой в качестве базы используется десять арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Базисом десятичной системой счисления является последовательность - ...10-3, 10-2, 10-1, 1, 10, 102, 103 ,…10n ...
Позиционные системы счисления, в которых для всех разрядов числа используется одинаковое основание (базис в соседних разрядах меняются в одинаковое количество раз — в р раз), называются однородными. В любой однородной системе счисления с натуральным основанием р базисом является числовая последовательность
...,p-3, р-2, р-1, р0 = 1, р1 ,р2, р3, ...,рn,...,
которая является геометрической прогрессией со знаменателем равным основанию системы счисления р.
Применяются также позиционные системы счисления, в которых в качестве базиса используется некоторая числовая последовательность, но она не является геометрической прогрессией. Такие системы счисления называются неоднородными. Примерами неоднородных систем счисления могут быть фибоначчиевая система и факториальная система. В фибоначчиевой системе в качестве базиса используются числа последовательности Фибоначчи - 1,2,3,5,8,13,..., и далее по закону
аn=аn-1 + an-2, а алфавитом в этой системе счисления являются цифры 0, 1. В факториальной системе в качестве базиса используются факториалы натуральных чисел –
1! = 1, 2! = 2, 3!=6 (n-1)!, n!, где факториал числа л (обозначается n!) вычисляется по формуле n!=l*2*3..(n-l)*n. Для каждого разряда в этой системе используется определенный набор цифр из алфавита системы.
Существуют и другие позиционные системы счисления. Широкое распространение имела двенадцатеричная система счисления, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки. Остатки двенадцатеричная системы счисления до сих пор используются в устной речи и обычаях. Хорошо известно, например, название единицы второго разряда в двенадцатеричной системе счисления - числа 12 - дюжина. Сохранился обычай считать многие предметы не десятками, а дюжинами. Например, столовые приборы и сервизе или стулья в мебельном гарнитуре (12 стульев - дюжина стульев, 6 тарелок - полдюжины тарелок), число месяцев в году, в сутках две дюжины часов и т.д. Название единицы третьего разряда в двенадцатеричной системе счисления - гросс - встречается теперь редко (наверное, только в кроссвордах), но в торговой практике начала столетия оно бытовало, и его можно было легко встретить. В 1928 году В.В.Маяковский в стихотворении "Плюшкин" писал «… укупил двенадцать гроссов дирижерских палочек».
Использовались и другие системы счисления. В Древнем Китае применялась пятеричная система счисления, в Центральной Америке у древних кельтов - 20-ричная система счисления, в Вавилоне - 6-ричная, которая используется до сих пор при оперировании и измерении времени и угловых величии.
При представлении чисел в позиционной системе счислений с любым основанием для однородных систем счисления нулевому разряду (позиция единиц) соответствует младший разряд целой части числа. Номер каждого следующего разряда числа, расположенного слева от запятой (целой частью числа) увеличивается на единицу, а разряд числа, расположенного справа от запятой (дробной частью числа) уменьшается на единицу. Номер разряда показывает, в какую степень надо возвести основание системы счисления.
Для систем с основанием меньшим десяти можно использовать те же цифры, что и в десятичной системе. В этом случае, надо указывать в какой именно системе счисления записано число. В дальнейшем, при рассмотрении задач, связанных с системами счислений, основание числа записывать в виде индекса справа от числа, либо указывать основание справа от числа в скобках. Само основание, в этом случае, пишется в десятичной системе счисления. Например, десятичное число 1928 может быть обозначено как 1928
(10) 1342(5) означает, что число записано в пятеричной системе, а 5324(7) означает, что число записано в семеричной системе.
В позиционной системе счисления с натуральным основанием р должно быть использовано ровно р различных цифр. В любой позиционной системе счисления с натуральным основанием число равное основанию системы записывается в виде 10, поскольку основание есть единица первого разряда, но надо помнить, что эта десятка имеет различное количественное значение в различных системах счисления.
Правила представления чисел в позиционных системах счисления
В однородной системе счисления с основанием р положительное смешанное число А(р) записывается в виде последовательности р-ичпых цифр, разделенных запятой на две последовательности, которые выражают целую и дробную части соответственно:
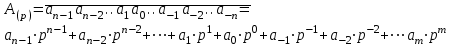
Вторая строчка равенства называется степенным рядом либо развернутой формой записи числа. Первая строчка называется свернутой формой, которая наиболее употребима. Степенной ряд или данное число можно коротко записать в виде
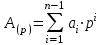где р - основание системы счисления; 
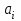- цифра в i-ом разряде; n, m - число позиций (разрядов), соответственно, для целой и дробной части числа. m - наименьший разряд в дробной части числа, а также точность приближенного представления числа. Черта над цифрами означает, что это не произведение всех чисел, записанных с помощью цифр, а именно одно число, записанное с помощью этих цифр. Иногда, в дальнейшем, эту черту будем опускать, когда из контекста ясно, что мы имеем дело с многоразрядными числами.Сами цифры и их обозначения берутся из алфавита, который содержит р символов. Каждой цифре соответствует определенный количественный эквивалент - числовое значение. В большинстве случаев для любой цифры, входящей в такую систему счисления, выполняется неравенство
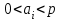
Из формулы следует, что в любой однородной позиционной системе счисления число можно представить как сумму произведений цифр этого числа на основание системы счисления в некоторой степени.