Файл: Курс лекций по дисциплине Цифровая схемотехника для специальности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 129
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Существуют системы счисления, в которых это соотношение не выполняется. Например, в системах, с так называемым, симметрическим или кососимметричным алфавитом. Поясним что это такое. Если в системе с основанием р множество цифр состоит из элементов {0,1…р=1}, то говорят, что система имеет естественное множество цифр; если р=2m+1 и множество цифр равно {-m,....,-1,0,1,....,m], то говорят, что система имеет симметрическое множество цифр, если р = 2m и множество цифр равно {-m....,-1,0,1, ....,m-1} или {-m + 1,....-1,0,1,....m}, то говорят, что система имеет кососимметрическое в отрицательную или положительную сторону множество цифр, соответственно.
Показатели степени основания дробной части -m могут изображаться отрицательными числами от -1до -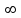 (из арифметики и алгебры известно, что дробная часть может выражаться с помощью бесконечной периодической или непериодической дроби).
(из арифметики и алгебры известно, что дробная часть может выражаться с помощью бесконечной периодической или непериодической дроби).
Для некоторых, часто встречающихся, систем счислений применяются следующие алфавиты или цифры:
в 2 СС - {0, 1),
в 3 СС – {0, 1, 2} или {1; 0;1} - симметричный алфавит,
в 8СС- {0, 1, 2, 3, 4, 5, 6, 7},
в 10 СС - {0, 1. 2, 3, 4. 5, 6, 7, 8, 9}
в 16 СС - {0, 1. 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, Е, F}.
Приведем примеры записи целых, дробных и смешанных чисел в различных системах счислений. Например,
0,CD16=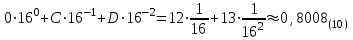
Эти примеры показывают, что некоторое число можно записать в различных системах счисления. Любое число можно записать в системе счисления с любым основанием.
В современных ЭВМ используются двоичная, восьмеричная, шестнадцатеричная и, конечно, привычная нам, десятичная системы счисления. Для каждой системы используется свой алфавит - набор цифр для изображения чисел. Рассмотрим более подробно представление чисел в применяемых в ЭВМ двоичной, восьмеричной н шестнадцатеричной системах счисления.
Имеет цифровой набор {0,1/}, р=2. В двоичной системе 102 = 210. Иногда вместо индекса 2 для обозначения двоичных чисел используется латинская буква b (binary). Например, 11011b. Смешанное двоичное число можно представить выражением в десятичной системе счисления
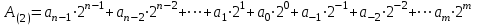
В соответствии с этой формулой целое двоичное число 1000101(2) можно записать следующим образом:
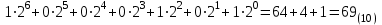
Смешанное двоичное число 10011,0101(2) можно записать следующим образом:
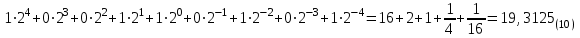 Двоичная система счисления очень широко используется в ЭВМ, поэтому полезно знать наиболее часто встречающиеся степени числа 2. В таблице 2.1.1 приведены первые 12 степеней числа 2
Двоичная система счисления очень широко используется в ЭВМ, поэтому полезно знать наиболее часто встречающиеся степени числа 2. В таблице 2.1.1 приведены первые 12 степеней числа 2
Таблица 2.1.1
Для изображения чисел в восьмеричной системе используются первые 8 цифр десятичной системы счисления - {0,1, 2,3,4,5,6,7}, р = 8. В восьмеричной системе 108 = 810.
В восьмеричной системе счисления, целое число 53758 имеет вид:
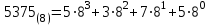
=2813(10)
Для изображения чисел в шестнадцатеричной системе требуется 16 цифр. Первые десять цифр берутся из десятичной системы счисления, а для шести остальных используются шесть заглавных (прописных) букв латинского алфавита - А, В, С, D, Е, F. Заметим, что можно было бы использовать любые другие шесть символов - например, 1,2,3,4,5,6.
Таким образом, в шестнадцатеричной системе имеется набор цифр {0, 1. 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, Е, F}, р=16. В шестнадцатеричной системе 1016 = 1610.
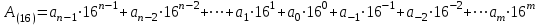
Приведем еще несколько примеров записи целых и дробных шестнадцатеричных чисел.
1АА9,С(16)=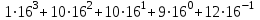 = 426,5625
= 426,5625
Полезно знать соответствие одинаковых чисел в указанных системах счисления и десятичной системе счисления, которая является наиболее удобной для проведения операций с числами и их восприятия. В таблице 2 1.2 приведены представления десятичных числа от 0 до 21 в двоичной, восьмеричной и шестнадцатеричной системах счисления.
Таблица 2,1.2
Перевод десятичных чисел в другие системы счисления
Перевод целых чисел
Алгоритм перевода (последовательность шагов):
Пример 1: Перевести число 37 из десятичной в двоичную систему счисления. (Ответ: 3710 = 1001012).
37 : 2 = 18 + 1, значит a0 = 1,
18 : 2 = 9 + 0, значит a1 = 0,
9 : 2 = 4 + 1, значит a2 = 1,
4 : 2 = 2 + 0, значит a3 = 0,
2 : 2 = 1 + 0, значит a4 = 0,
1 < 2, следовательно, деление следует прекратить, а полученная цифра – это a5 = 1.
Теперь составим число a5 a4 a3 a2 a1 a0 =1001012
Пример 2: Перевести число 315 из десятичной в восьмеричную систему счисления. (Ответ: 31510 = 4738).
315 : 8 = 39 + 3, значит a0 = 3,
39 : 8 = 4 + 7, значит a1 = 7,
4 < 7, следовательно, деление следует прекратить, а полученная цифра – это a2 = 4.
Теперь составим число a2a1a0 = 4738
Пример 3: Перевести число 315 из десятичной в шестнадцатеричную систему счисления. (Ответ: 31510 = 13B16).
315 : 16 = 19 + 11, значит a0 = 11,
19 : 16 = 1 + 3, значит a1 = 3,
1 < 16, следовательно, деление следует прекратить, а полученная цифра – это a2 = 1.
Теперь составим число a2a1a0 = 13B16
Перевод правильных дробей
Алгоритм перевода:
Пример 1: Перевести число 0,1875 из десятичной в двоичную систему счисления. (Ответ: 0,1875 10 = 0,00112).
Теперь составим число 0,a-1a-2a-3 = 0, 00112
Пример 2: Перевести число 0,1875 из десятичной в восьмеричную систему счисления. (Ответ: 0,1875 10 = 0,148).
Теперь составим число 0,a-1a-2= 0, 148
Пример 3: Перевести число 0,1875 из десятичной в шестнацатеричную систему счисления. (Ответ: 0,1875 10 = 0,316).
Теперь составим число 0,a-1= 0, 316
Перевод смешанных чисел
Правило перевода: целая и дробная часть исходного числа переводятся отдельно по рассмотренным выше алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример: 315,187510 = 473,148 = 13B,316
Перевод чисел из любой позиционной системы счисления в десятичную
Алгоритм перевода:
Показатели степени основания дробной части -m могут изображаться отрицательными числами от -1до -
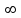 (из арифметики и алгебры известно, что дробная часть может выражаться с помощью бесконечной периодической или непериодической дроби).
(из арифметики и алгебры известно, что дробная часть может выражаться с помощью бесконечной периодической или непериодической дроби).Для некоторых, часто встречающихся, систем счислений применяются следующие алфавиты или цифры:
в 2 СС - {0, 1),
в 3 СС – {0, 1, 2} или {1; 0;1} - симметричный алфавит,
в 8СС- {0, 1, 2, 3, 4, 5, 6, 7},
в 10 СС - {0, 1. 2, 3, 4. 5, 6, 7, 8, 9}
в 16 СС - {0, 1. 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, Е, F}.
Приведем примеры записи целых, дробных и смешанных чисел в различных системах счислений. Например,
0,CD16=
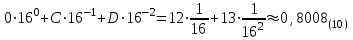
Эти примеры показывают, что некоторое число можно записать в различных системах счисления. Любое число можно записать в системе счисления с любым основанием.
В современных ЭВМ используются двоичная, восьмеричная, шестнадцатеричная и, конечно, привычная нам, десятичная системы счисления. Для каждой системы используется свой алфавит - набор цифр для изображения чисел. Рассмотрим более подробно представление чисел в применяемых в ЭВМ двоичной, восьмеричной н шестнадцатеричной системах счисления.
Двоичная система счисления (бинарная или диодная система счисления)
Имеет цифровой набор {0,1/}, р=2. В двоичной системе 102 = 210. Иногда вместо индекса 2 для обозначения двоичных чисел используется латинская буква b (binary). Например, 11011b. Смешанное двоичное число можно представить выражением в десятичной системе счисления
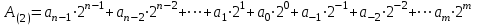
В соответствии с этой формулой целое двоичное число 1000101(2) можно записать следующим образом:
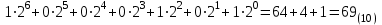
Смешанное двоичное число 10011,0101(2) можно записать следующим образом:
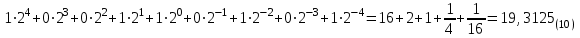 Двоичная система счисления очень широко используется в ЭВМ, поэтому полезно знать наиболее часто встречающиеся степени числа 2. В таблице 2.1.1 приведены первые 12 степеней числа 2
Двоичная система счисления очень широко используется в ЭВМ, поэтому полезно знать наиболее часто встречающиеся степени числа 2. В таблице 2.1.1 приведены первые 12 степеней числа 2Таблица 2.1.1
| к | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2к | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
Восьмеричная система счисления
Для изображения чисел в восьмеричной системе используются первые 8 цифр десятичной системы счисления - {0,1, 2,3,4,5,6,7}, р = 8. В восьмеричной системе 108 = 810.
В восьмеричной системе счисления, целое число 53758 имеет вид:
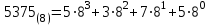
=2813(10)
Шестнадцатеричная система счисления
Для изображения чисел в шестнадцатеричной системе требуется 16 цифр. Первые десять цифр берутся из десятичной системы счисления, а для шести остальных используются шесть заглавных (прописных) букв латинского алфавита - А, В, С, D, Е, F. Заметим, что можно было бы использовать любые другие шесть символов - например, 1,2,3,4,5,6.
Таким образом, в шестнадцатеричной системе имеется набор цифр {0, 1. 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, Е, F}, р=16. В шестнадцатеричной системе 1016 = 1610.
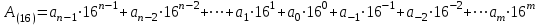
Приведем еще несколько примеров записи целых и дробных шестнадцатеричных чисел.
1АА9,С(16)=
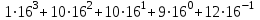 = 426,5625
= 426,5625Полезно знать соответствие одинаковых чисел в указанных системах счисления и десятичной системе счисления, которая является наиболее удобной для проведения операций с числами и их восприятия. В таблице 2 1.2 приведены представления десятичных числа от 0 до 21 в двоичной, восьмеричной и шестнадцатеричной системах счисления.
Таблица 2,1.2
| Эквиваленты в системах счисления | Эквиваленты в системах счисления | ||||||
| 10 СС | 2 СС | 8 СС | 16 СС | 10СС | 2СС | 8 СС | 16 СС |
| 0 | 0 | 0 | 0 | 11 | 1011 | 13 | В |
| 1 | 1 | 1 | 1 | 12 | 1100 | 14 | С |
| 2 | 10 | 2 | 2 | 13 | 1101 | 15 | D |
| 3 | 11 | 3 | 3 | 14 | 1110 | 16 | Е |
| 4 | 100 | 4 | 4 | 15 | 1111 | 17 | F |
| 5 | 101 | 5 | 5 | 16 | 10000 | 20 | 10 |
| 6 | 110 | 6 | 6 | 17 | 10001 | 21 | 11 |
| 7 | 111 | 7 | 7 | 18 | 10010 | 22 | 12 |
| 8 | 1000 | 10 | 8 | 19 | 10011 | 23 | 13 |
| 9 | 1001 | 11 | 9 | 20 | 10100 | 24 | 14 |
| 10 | 1010 | 12 | А | 21 | 10101 | 25 | 15 |
-
Преобразование чисел из одной системы в другую
Перевод десятичных чисел в другие системы счисления
Перевод целых чисел
Алгоритм перевода (последовательность шагов):
-
Основание новой системы счисления выразить в десятичной с.с. и все последующие действия выполнять в десятичной с.с. -
Последовательно выполнять деление данного числа и получаемых промежуточных частных на основание новой с.с. до тех пор, пока не будет получено частное, меньшее делителя. -
Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления. -
Составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример 1: Перевести число 37 из десятичной в двоичную систему счисления. (Ответ: 3710 = 1001012).
37 : 2 = 18 + 1, значит a0 = 1,
18 : 2 = 9 + 0, значит a1 = 0,
9 : 2 = 4 + 1, значит a2 = 1,
4 : 2 = 2 + 0, значит a3 = 0,
2 : 2 = 1 + 0, значит a4 = 0,
1 < 2, следовательно, деление следует прекратить, а полученная цифра – это a5 = 1.
Теперь составим число a5 a4 a3 a2 a1 a0 =1001012
Пример 2: Перевести число 315 из десятичной в восьмеричную систему счисления. (Ответ: 31510 = 4738).
315 : 8 = 39 + 3, значит a0 = 3,
39 : 8 = 4 + 7, значит a1 = 7,
4 < 7, следовательно, деление следует прекратить, а полученная цифра – это a2 = 4.
Теперь составим число a2a1a0 = 4738
Пример 3: Перевести число 315 из десятичной в шестнадцатеричную систему счисления. (Ответ: 31510 = 13B16).
315 : 16 = 19 + 11, значит a0 = 11,
19 : 16 = 1 + 3, значит a1 = 3,
1 < 16, следовательно, деление следует прекратить, а полученная цифра – это a2 = 1.
Теперь составим число a2a1a0 = 13B16
Перевод правильных дробей
Алгоритм перевода:
-
Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной с.с. -
Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления. -
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления. -
Составить дробную часть числа в новой системе счисления, записывая его, начиная с целой части первого произведения.
Пример 1: Перевести число 0,1875 из десятичной в двоичную систему счисления. (Ответ: 0,1875 10 = 0,00112).
| 0 | 1875 2 |
| a-1 = 0 | 3750 2 |
| a-2 = 0 | 7500 2 |
| a-3 = 1 | 5000 2 |
| a-4 = 1 | 0000 |
Теперь составим число 0,a-1a-2a-3 = 0, 00112
Пример 2: Перевести число 0,1875 из десятичной в восьмеричную систему счисления. (Ответ: 0,1875 10 = 0,148).
| 0 | 1875 8 |
| a-1 = 1 | 5000 8 |
| a-2 = 4 | 0000 |
Теперь составим число 0,a-1a-2= 0, 148
Пример 3: Перевести число 0,1875 из десятичной в шестнацатеричную систему счисления. (Ответ: 0,1875 10 = 0,316).
| 0 | 1875 16 |
| + 1 1 | 1250 8750 |
| a-1 = 3 | 0000 |
Теперь составим число 0,a-1= 0, 316
Перевод смешанных чисел
Правило перевода: целая и дробная часть исходного числа переводятся отдельно по рассмотренным выше алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример: 315,187510 = 473,148 = 13B,316
Перевод чисел из любой позиционной системы счисления в десятичную
Алгоритм перевода:
-
Расставить значения степеней основания системы счисления для каждой значащей цифры числа. -
Цифры числа в исходной системе счисления привести в соответствие с алфавитом десятичной системы счисления. -
Основание исходной системы счисления выразить в десятичной с.с. и все последующие действия выполнять в десятичной с.с. -
Записать число в развернутой форме и выполнить необходимые арифметические действия.
