Файл: Курсовая работа по учебному курсу Теория механизмов и машин.docx

М инистерство образования и науки Российской Федерации
федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»

КУРСОВАЯ РАБОТА

по учебному курсу «Теория механизмов и машин»

Вариант 14

Студент	Онищенко С.А. (И.О. Фамилия)
Группа	ТБбп-2006а
Ассистент	(И.О. Фамилия)
Преподаватель	Балахнина А.А. (И.О. Фамилия)

Тольятти 2022

Оглавление

1. Кинематический анализ механизма

   1. Исходные данные

ВАРИАНТ 5
Тема 1
Кинематическая схема механизма	Число оборотов кривошипа nОА (об/мин)	Размеры звеньев и расстояния, мм.
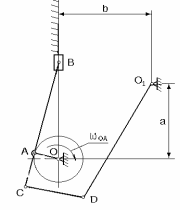	550	lОА = 95 lАB = 475 lВC = 540 lCD = 160 lDО1 = 210 a = 160 b = 120

---

2. Структурный анализ механизма

На рисунке 1.1 Изобразим структурную схему механизма



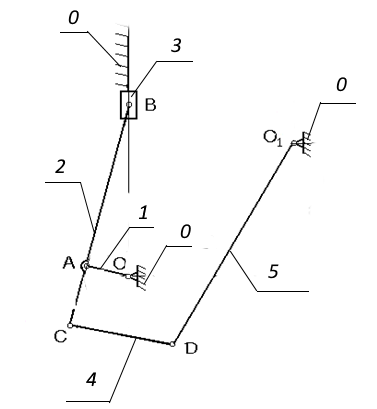
Рис. 1.1 Структурная схема

Далее проведем структурный анализ механизма.

Составим описание звеньев и кинематических пар механизма и занесём их соответственно в таблицу 1.1 и таблицу 1.2.

Таблица 1.1Характеристика звеньев механизма

№	Характер движения	Название
1	Вращательное	Кривошип
2	Плоскопараллельное	Шатун
3	Поступательное	Ползун
4	Плоскопараллельное	Шатун
5	Плоскопараллельное	Коромысло
0	Неподвижное	Стойка

Таблица 1.2 Кинематические пары механизма

№ -№	Звенья в пары	Тип пары	Класс
1	стойка 0 – кривошип 1	вращательная	5
2	кривошип 1 –шатун 2	вращательная	5
3	шатун 2 – ползун 3	вращательная	5
4	ползун  3 – стойка 0	поступательная	5
5	шатун 2 –шатун 4	вращательная	5
6	шатун 4 – коромысло 5	вращательная	5
7	коромысло  5 – стойка 0	вращательная	5

Степень свободы плоского механизма находится по формуле Чебышева

---

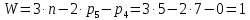
где n – число подвижных звеньев, в данном механизме их 5 (табл. 1.1);

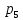– число кинематических пар 5 класса, в данном механизме их 7 (табл. 1.2);

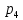– количество пар 4 класса, в данном механизме их нет (табл. 1.2).

3. Построение планов положений механизмов

На плане механизма отобразим входное звено ОА отрезком длиной 38 мм.

Масштабный коэффициент планов механизма:



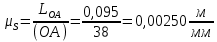
В принятом масштабе пересчитываем отрезки на чертеже:













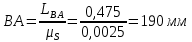
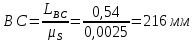
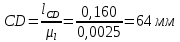
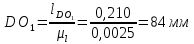
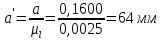
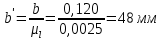
Находим крайнее положение, в котором кривошип и шатун вытянутся в одну линию и ползун занимает крайнюю верхнюю точку. От этого положения будем отсчитывать остальные положения. Отмечаем положения кривошипа с шагом 30 градусов.

Рассмотрим построение второго положения. Наносим на чертеже все неподвижные оси: шарниры О, О₁ и линию движения ползуна В. Из точки О проводим отрезок длинной кривошипа АО, из точки А проводим засечку до линии движения ползуна 3 Таким образом находим точку B. По пропорции находим точку С. Из точки С - дугу окружности радиусом DC. Из точки O₁ - дугу окружности радиусом DO₁. Таким образом находим точку D.

4. Построение планов скоростей .

Рассмотрим построение плана скоростей на примере пятого положения механизма. Угловая скорость начального звена ОА:



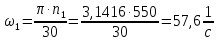
Скорость точки А:

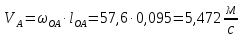
Скорости остальных точек механизма находим путём построения плана скоростей. Принимаем длину отрезка 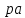, изображающего скорость 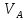точки А, равной 109,5 мм. Тогда масштаб плана скоростей:

---

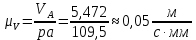
Рассматривая движение точки В вместе с точкой А и относительно этой точки, получим векторные уравнения для построения скорости точки



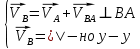
где V_ВА - скорость точки А во вращательном движении относительно точки В, направлена перпендикулярно оси звена АВ;

Из точки а проводим линию, перпендикулярную оси звена АВ, а из полюса P плана скоростей - линию, вертикальную линию по оси Y. Точка b пересечения этих линий даст конец вектора искомой скорости V_В . Скорость точкиCопределяем по правилу подобия:



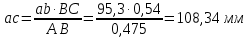
Определяем скорость точки D путем графического решения следующих векторных равенств:



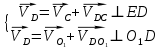
где V_DC - скорость точки D во вращательном движении относительно точки C, направлена перпендикулярно оси звена CD;

где V_DO1 - скорость точки D во вращательном движении относительно точки O₁, направлена перпендикулярно оси звена O₁D;

Из точки c проводим линию, перпендикулярную оси звена CD, а из полюса P плана скоростей - проводим линию, перпендикулярную оси звена O₁D. Точка dпересечения этих линий даст конец вектора искомой скорости V_D. Определим значения всех скоростей







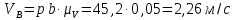
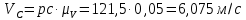
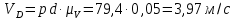
Определение угловых скоростей звеньев:







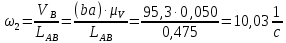
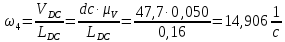
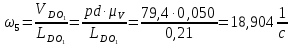
Значения для начального положения

---

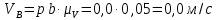
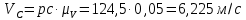
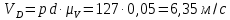
Определение угловых скоростей звеньев:

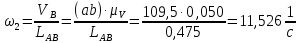
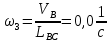
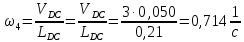
5. Построение планов ускорений

Точка А кривошипа будет иметь только нормальное ускорение, величина которого равна:



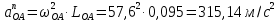
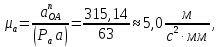
Рассматривая движение точки В вместе с точками А и С (относительное движение) и относительно этих точек, получаю векторные уравнения для построения ускорения точки В:



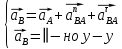
где a_ВАⁿ – нормальное ускорение точки В вокруг А, направленное //-но AB;

a_BА^τ - тангенциальное ускорение точки В вокруг А, направленное перпендикулярно AB;

a_А = ускорение точки А;





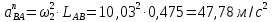
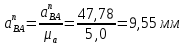
На плане ускорений через точку а вектора πa проводим прямую, ||-но оси звена АB, и откладываем на ней в направлении от точки A к точке B отрезок нормального ускорения. Через конец этого вектора проводим прямую, перпендикулярноно к оси звена АВ. Затем через полюс π проводим отрезок параллельно оси Y-Y. Точка пересечения этих прямых определит конец вектора πb. Точку C на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков, аналогично плану скоростей.

Ускорение точки D



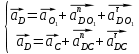
где a_DCⁿ - нормальное ускорение точки Dшатуна DC при вращении его вокруг точки C, направлено вдоль оси звена DC от точки D к точке C;

a_DC^τ – тангенциальное ускорение точки D шатуна DC при вращении его вокруг точки C, направленное перпендикулярно звену DC;

Величина нормального ускорения a_DCⁿ определяется по формуле:





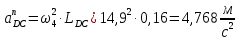
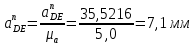
a_DOⁿ – нормальное ускорение точки D вокруг О₁, направленное //-но О

---