Файл: Курсовая работа по учебному курсу Теория механизмов и машин.docx
Добавлен: 28.03.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1D;
aDOτ,- тангенциальное ускорение точки D вокруг О1, направленное перпендикулярно DО1;
aO = ускорение опоры О1;

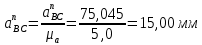
На плане ускорений через точку с вектора πс проводим прямую, параллельную оси звена СD, и откладываем на ней в направлении от точки D к точке С отрезок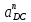 . Через конец этого вектора проводим прямую, перпендикулярную к оси звена СD. Затем через полюс π проводим прямую, параллельную оси звена О1D, и откладываем на ней в направлении от точки D к точке О1отрезок
. Через конец этого вектора проводим прямую, перпендикулярную к оси звена СD. Затем через полюс π проводим прямую, параллельную оси звена О1D, и откладываем на ней в направлении от точки D к точке О1отрезок 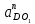 . Через конец этого вектора проводим прямую, перпендикулярную к оси звена О1D. Точка пересечения этих прямых определит конец вектора πd.
. Через конец этого вектора проводим прямую, перпендикулярную к оси звена О1D. Точка пересечения этих прямых определит конец вектора πd.
Определим значения всех ускорений
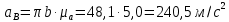
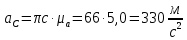
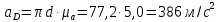
Определение угловых ускорений звеньев
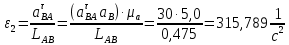
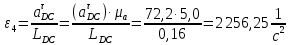
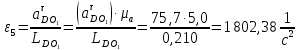
Значения для начального положения
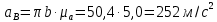

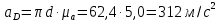
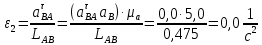
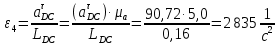

Начнем построение графика перемещения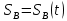 .
.
По найденным на планах механизма положениям ведомого звена 3 вычерчиваем график перемещения ползуна B, начиная от крайнего левого положения, при движении его вправо. По оси изменения угла поворота отложим отрезок L = 180 мм, разобьём его на 12 частей. Вычисление масштабов графика перемещений, так как
ординаты графика перемещений равны расстояниям, измеренным на планах механизма, то и масштаб графика равен масштабу схемы механизма, т. е.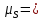 0,0025 м/мм. Откладываем положения ползуна в масштабе. После полученные точки соединяем плавной кривой. Строим оси координат и на оси абсцисс откладываем отрезок х = 150 мм который отображает время Т одного полного оборота кривошипа:
0,0025 м/мм. Откладываем положения ползуна в масштабе. После полученные точки соединяем плавной кривой. Строим оси координат и на оси абсцисс откладываем отрезок х = 150 мм который отображает время Т одного полного оборота кривошипа:
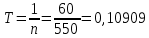 сек.
сек.
Определяем масштаб оси абсцисс:
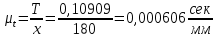 ;
;
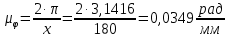 .
.
Для построения диаграммы скоростей точки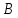 применим метод графического дифференцирования - метод хорд.На всех участках графика перемещений заменяем дуги хордами. Строим координатные оси (V,). По оси абсцисс откладываем отрезок
применим метод графического дифференцирования - метод хорд.На всех участках графика перемещений заменяем дуги хордами. Строим координатные оси (V,). По оси абсцисс откладываем отрезок 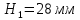 . Из конца этого отрезка Р проводим лучи до пересечения с осью ординат. Точки диаграммы скорости будут лежать на пересечении прямых, проходящих через точки пересечения лучей с осью ординат и параллельных оси абсцисс с соответствующими прямыми, параллельными оси ординат, проведенных через середины участков 1–2, 2–3, …, 12–1.
. Из конца этого отрезка Р проводим лучи до пересечения с осью ординат. Точки диаграммы скорости будут лежать на пересечении прямых, проходящих через точки пересечения лучей с осью ординат и параллельных оси абсцисс с соответствующими прямыми, параллельными оси ординат, проведенных через середины участков 1–2, 2–3, …, 12–1.
Масштаб аналога скоростей будет равен: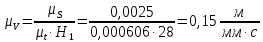 .
.
где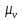 – масштабный коэффициент скорости на диаграмме, м·с-1/мм;
– масштабный коэффициент скорости на диаграмме, м·с-1/мм;
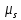 – масштабный коэффициент перемещений на диаграмме, м/мм;
– масштабный коэффициент перемещений на диаграмме, м/мм;
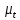 – масштабный коэффициент по времени, с/мм;
– масштабный коэффициент по времени, с/мм;
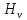 – полюсное расстояние, мм.
– полюсное расстояние, мм.
Для построения диаграммы ускорений точки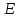
применим метод графического дифференцирования - метод хорд.
Построение аналогично построению диаграммы скоростей.
Для построения диаграммы ускорений выберем отрезок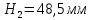 , тогда масштаб аналога ускорений будет равен:
, тогда масштаб аналога ускорений будет равен: 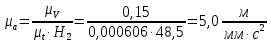 .
.
где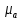 – масштаб диаграммы ускорения на диаграмме, м·с-2/мм;
– масштаб диаграммы ускорения на диаграмме, м·с-2/мм;
 – масштаб диаграммы скорости на диаграмме, м·с-1/мм;
– масштаб диаграммы скорости на диаграмме, м·с-1/мм;
 – масштабный коэффициент по времени, с/мм;
– масштабный коэффициент по времени, с/мм;
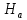 – полюсное расстояние, мм.
– полюсное расстояние, мм.
Значение скоростей и ускорений возьмем с диаграмм, умножив советующий отрезок на масштаб.
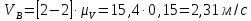
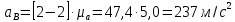
Проведем расчет погрешностей по формуле:
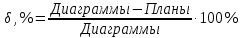
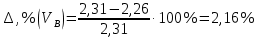
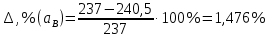
Строим график движения толкателя:
- фазовый угол удаления
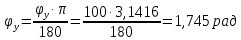
- фазовый угол дальнего выстоя
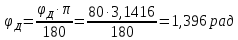
- фазовый угол возврата

Рабочий угол
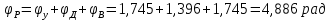
Масштаб по оси абсцисс
После чего подставляем полученные значения в формулу.

где L =200 мм - отрезок, изображающий рабочий угол кулачка.
Отрезки, изображающие фазовые углы:
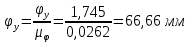
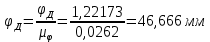
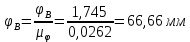
Откладываем произвольные отрезки, изображающие аналоги ускорений.
Определим радиус построения
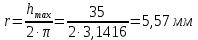
Проводим половину окружности, которую делим на 4 равных частей. Из точек деления проводим прямые, параллельные оси φ до пересечения с осью S получаем точки пересечения. Далее проводим отрезок из начала координат то первой точки верхнего выстоя. Из полученных ранее точек пересечения проводим отрезки параллельные ему. Получаем график перемещения
Проводим полуокружность с центром равным расстоянию радиуса отложенного от начало оси угла поворота. Определим радиус.
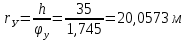
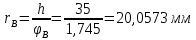
В масштабе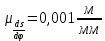 , будем использовать полученные радиусы.
, будем использовать полученные радиусы.
Проводим четверть окружности, которую делим на 4 равных части. Из точек деления проводим прямые, параллельные оси φ до пересечения с соответствующими ординатами. Точки пересечения соединяем главной кривой. Для фазы приближения построение кривой аналогично.
Из начала координат радиусом
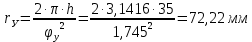
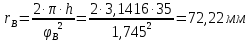
В масштабе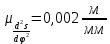 , будем использовать радиус 36,1 мм. Проводим полуокружность и разбиваем ее на 6 равных частей. Точки деления сносим параллельно оси φ до пересечения с соответствующими ординатами.
, будем использовать радиус 36,1 мм. Проводим полуокружность и разбиваем ее на 6 равных частей. Точки деления сносим параллельно оси φ до пересечения с соответствующими ординатами.
Построение профиля кулачка ведём методом обращённого движения.
Из произвольно выбранной точки О проводим дугу ОА в сторону подъема толкателя. Выбираем на этой дуге произвольно точку 1, которую примем за начальную точку отсчета.
Задаемся рядом последовательных значений фазового угла на участке удаления, подсчитываем соответствующие углы поворота толкателя и изображаем эти положения на рисунке откладываем полученные отрезки на соответствующих положениях. Направление, в котором следует откладывать величины, определяется по следующему правилу: вектор скорости точки А в соответствующем положении толкателя нужно повернуть на 90° в сторону вращения кулачка.
Аналогичные построения проводят и для фазы сближения толкателя.
Через ряд точек отмеченных на графике проводим лучи под углами γ mах для участка удаления и γ mаx для участка сближения к соответствующим положениям коромысла. По умолчанию примем данные углы сорока пяти градусам. Находим точку О пересечения лучей с разных сторон графика наиболее удаленную от точки 1. Эта точка и определит как минимальные габариты кулачкового механизма, так и зону допустимых размеров кулачкового механизма , обеспечивающих значения углов давления при любом положении кулачка, не превышающих допустимых значений. Находим RMIN = 25,5 мм, округляем 30 мм
В масштабе 0,030 м
Проектируем профиль кулачка, ориентируясь на схему кулачкового механизма, полученную ранее. Для кулачкового механизма должны быть известны радиус Rо основной шайбы, межосевое расстояние, длина коромысла LОА, направление вращения кулачка. Используя - метод обращенного вращения, сообщим всему кулачковому механизму угловую скорость «-ω». В результате кулачок становится неподвижным, а коромысло вместе со своей осью вращения О придет во вращение относительно центра О в направлении противоположном вращению кулачка. Делим фазовые углы на части в соответствии с произведенной разметкой хода толкателя показывая последовательно точки О2, О3, О4,... на окружности. Проводим последовательно дуги радиусами коромысла и находим точки 2', 3', 4', ... их пересечения, фиксируя тем самым соответствующие контактные точки кулачка и коромысла в обращенном механизме.
aDOτ,- тангенциальное ускорение точки D вокруг О1, направленное перпендикулярно DО1;
aO = ускорение опоры О1;

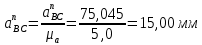
На плане ускорений через точку с вектора πс проводим прямую, параллельную оси звена СD, и откладываем на ней в направлении от точки D к точке С отрезок
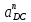 . Через конец этого вектора проводим прямую, перпендикулярную к оси звена СD. Затем через полюс π проводим прямую, параллельную оси звена О1D, и откладываем на ней в направлении от точки D к точке О1отрезок
. Через конец этого вектора проводим прямую, перпендикулярную к оси звена СD. Затем через полюс π проводим прямую, параллельную оси звена О1D, и откладываем на ней в направлении от точки D к точке О1отрезок 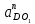 . Через конец этого вектора проводим прямую, перпендикулярную к оси звена О1D. Точка пересечения этих прямых определит конец вектора πd.
. Через конец этого вектора проводим прямую, перпендикулярную к оси звена О1D. Точка пересечения этих прямых определит конец вектора πd. Определим значения всех ускорений
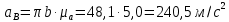
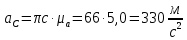
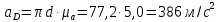
Определение угловых ускорений звеньев
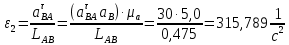
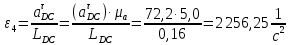
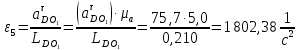
Значения для начального положения
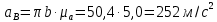

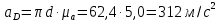
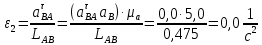
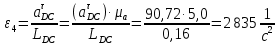

-
Построение кинематических диаграмм
-
Построение диаграмма перемещения ползуна
-
Начнем построение графика перемещения
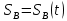 .
. По найденным на планах механизма положениям ведомого звена 3 вычерчиваем график перемещения ползуна B, начиная от крайнего левого положения, при движении его вправо. По оси изменения угла поворота отложим отрезок L = 180 мм, разобьём его на 12 частей. Вычисление масштабов графика перемещений, так как
ординаты графика перемещений равны расстояниям, измеренным на планах механизма, то и масштаб графика равен масштабу схемы механизма, т. е.
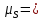 0,0025 м/мм. Откладываем положения ползуна в масштабе. После полученные точки соединяем плавной кривой. Строим оси координат и на оси абсцисс откладываем отрезок х = 150 мм который отображает время Т одного полного оборота кривошипа:
0,0025 м/мм. Откладываем положения ползуна в масштабе. После полученные точки соединяем плавной кривой. Строим оси координат и на оси абсцисс откладываем отрезок х = 150 мм который отображает время Т одного полного оборота кривошипа: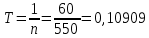 сек.
сек. Определяем масштаб оси абсцисс:
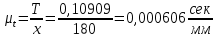 ;
;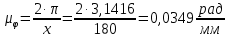 .
. -
Построение диаграмма скорости ползуна.
Для построения диаграммы скоростей точки
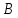 применим метод графического дифференцирования - метод хорд.На всех участках графика перемещений заменяем дуги хордами. Строим координатные оси (V,). По оси абсцисс откладываем отрезок
применим метод графического дифференцирования - метод хорд.На всех участках графика перемещений заменяем дуги хордами. Строим координатные оси (V,). По оси абсцисс откладываем отрезок 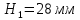 . Из конца этого отрезка Р проводим лучи до пересечения с осью ординат. Точки диаграммы скорости будут лежать на пересечении прямых, проходящих через точки пересечения лучей с осью ординат и параллельных оси абсцисс с соответствующими прямыми, параллельными оси ординат, проведенных через середины участков 1–2, 2–3, …, 12–1.
. Из конца этого отрезка Р проводим лучи до пересечения с осью ординат. Точки диаграммы скорости будут лежать на пересечении прямых, проходящих через точки пересечения лучей с осью ординат и параллельных оси абсцисс с соответствующими прямыми, параллельными оси ординат, проведенных через середины участков 1–2, 2–3, …, 12–1.Масштаб аналога скоростей будет равен:
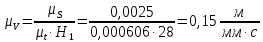 .
. где
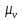 – масштабный коэффициент скорости на диаграмме, м·с-1/мм;
– масштабный коэффициент скорости на диаграмме, м·с-1/мм;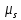 – масштабный коэффициент перемещений на диаграмме, м/мм;
– масштабный коэффициент перемещений на диаграмме, м/мм;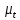 – масштабный коэффициент по времени, с/мм;
– масштабный коэффициент по времени, с/мм;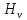 – полюсное расстояние, мм.
– полюсное расстояние, мм.-
Построение диаграмма ускорений ползуна.
Для построения диаграммы ускорений точки
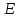
применим метод графического дифференцирования - метод хорд.
Построение аналогично построению диаграммы скоростей.
Для построения диаграммы ускорений выберем отрезок
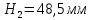 , тогда масштаб аналога ускорений будет равен:
, тогда масштаб аналога ускорений будет равен: 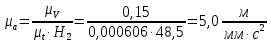 .
. где
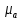 – масштаб диаграммы ускорения на диаграмме, м·с-2/мм;
– масштаб диаграммы ускорения на диаграмме, м·с-2/мм; – масштаб диаграммы скорости на диаграмме, м·с-1/мм;
– масштаб диаграммы скорости на диаграмме, м·с-1/мм; – масштабный коэффициент по времени, с/мм;
– масштабный коэффициент по времени, с/мм;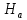 – полюсное расстояние, мм.
– полюсное расстояние, мм.-
Сравнительный анализ метода планов и метода диаграмм.
Значение скоростей и ускорений возьмем с диаграмм, умножив советующий отрезок на масштаб.
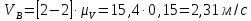
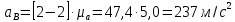
Проведем расчет погрешностей по формуле:
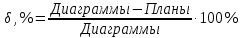
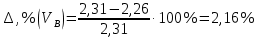
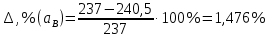
-
Динамический синтез кулачкового механизма
-
Исходные данные
-
| Тема 2 | ||
| Тип кулачкового механизма | Тип диаграммы ускорения толкателя | Исходные данные |
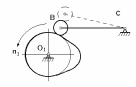 | 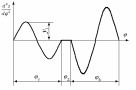 | 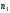 = 250 об/мин = 250 об/мин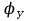 =100° =100°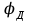 =80° =80°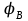 =100° =100°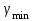 = 45° = 45°h = 35 мм lCB = 100 мм |
Строим график движения толкателя:
- фазовый угол удаления
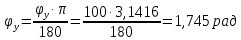
- фазовый угол дальнего выстоя
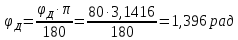
- фазовый угол возврата

Рабочий угол
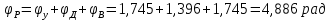
Масштаб по оси абсцисс
После чего подставляем полученные значения в формулу.

где L =200 мм - отрезок, изображающий рабочий угол кулачка.
Отрезки, изображающие фазовые углы:
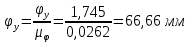
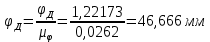
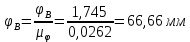
Откладываем произвольные отрезки, изображающие аналоги ускорений.
-
Построение диаграмм
-
Диаграмма перемещений
-
Определим радиус построения
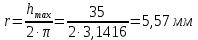
Проводим половину окружности, которую делим на 4 равных частей. Из точек деления проводим прямые, параллельные оси φ до пересечения с осью S получаем точки пересечения. Далее проводим отрезок из начала координат то первой точки верхнего выстоя. Из полученных ранее точек пересечения проводим отрезки параллельные ему. Получаем график перемещения
-
Диаграмма скоростей
Проводим полуокружность с центром равным расстоянию радиуса отложенного от начало оси угла поворота. Определим радиус.
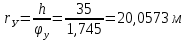
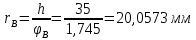
В масштабе
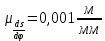 , будем использовать полученные радиусы.
, будем использовать полученные радиусы. Проводим четверть окружности, которую делим на 4 равных части. Из точек деления проводим прямые, параллельные оси φ до пересечения с соответствующими ординатами. Точки пересечения соединяем главной кривой. Для фазы приближения построение кривой аналогично.
-
Диаграмма ускорений
Из начала координат радиусом
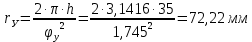
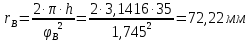
В масштабе
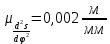 , будем использовать радиус 36,1 мм. Проводим полуокружность и разбиваем ее на 6 равных частей. Точки деления сносим параллельно оси φ до пересечения с соответствующими ординатами.
, будем использовать радиус 36,1 мм. Проводим полуокружность и разбиваем ее на 6 равных частей. Точки деления сносим параллельно оси φ до пересечения с соответствующими ординатами. Построение профиля кулачка ведём методом обращённого движения.
-
Построение профиля кулачка.
Из произвольно выбранной точки О проводим дугу ОА в сторону подъема толкателя. Выбираем на этой дуге произвольно точку 1, которую примем за начальную точку отсчета.
Задаемся рядом последовательных значений фазового угла на участке удаления, подсчитываем соответствующие углы поворота толкателя и изображаем эти положения на рисунке откладываем полученные отрезки на соответствующих положениях. Направление, в котором следует откладывать величины, определяется по следующему правилу: вектор скорости точки А в соответствующем положении толкателя нужно повернуть на 90° в сторону вращения кулачка.
Аналогичные построения проводят и для фазы сближения толкателя.
Через ряд точек отмеченных на графике проводим лучи под углами γ mах для участка удаления и γ mаx для участка сближения к соответствующим положениям коромысла. По умолчанию примем данные углы сорока пяти градусам. Находим точку О пересечения лучей с разных сторон графика наиболее удаленную от точки 1. Эта точка и определит как минимальные габариты кулачкового механизма, так и зону допустимых размеров кулачкового механизма , обеспечивающих значения углов давления при любом положении кулачка, не превышающих допустимых значений. Находим RMIN = 25,5 мм, округляем 30 мм
В масштабе 0,030 м
Проектируем профиль кулачка, ориентируясь на схему кулачкового механизма, полученную ранее. Для кулачкового механизма должны быть известны радиус Rо основной шайбы, межосевое расстояние, длина коромысла LОА, направление вращения кулачка. Используя - метод обращенного вращения, сообщим всему кулачковому механизму угловую скорость «-ω». В результате кулачок становится неподвижным, а коромысло вместе со своей осью вращения О придет во вращение относительно центра О в направлении противоположном вращению кулачка. Делим фазовые углы на части в соответствии с произведенной разметкой хода толкателя показывая последовательно точки О2, О3, О4,... на окружности. Проводим последовательно дуги радиусами коромысла и находим точки 2', 3', 4', ... их пересечения, фиксируя тем самым соответствующие контактные точки кулачка и коромысла в обращенном механизме.

