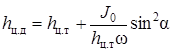(20)

где hц.д = yц.д sin - глубина погружения центра давления.

Решить задачу:

Определить на какой высоте z установится уровень ртути в сосуде относительно точки А, если манометрическое (избыточное) давление в этой точке составляет P_a=1,1 Атм . Жидкости находится в равновесии. Плотность ртути принять равной 13 600 кг/м³ , воды 990 кг/м³ . Значение высоты h=45 см.
Решение
Абсолютное (полное) гидростатическое давление находится как сумма давления, приложенного к поверхности жидкости (P0), и давления столба жидкости (Pизб) высотой, равной глубине погружения клапана.
Р_абс=Р₀+Р_изб=Р₀+????????ℎ,[Па]
где P₀ – давление, приложенное к поверхности жидкости, Па; ???? - плотность жидкости, кгм³; g – ускорение свободного падения, м/с²; h – высота столба жидкости, м.
Р_абс=Р₀+Р_а= Р₀+????_рт????ℎ+????_ж????z , где Р₀=0,

тогда Р_а= ????_рт????ℎ+????_ж????z,

z= (Р_а - ????_рт????ℎ)/????_ж????= (111457 -(13600*10*0,45))/(990*10) =5,08 м.
Задание 5
Ответить на теоретические вопросы:
1.Как определяется средняя скорость в живом сечении потока? Что такое гидравлический радиус и гидравлический диаметр и зачем введены эти понятия? Чем отличается равномерное движение от неравномерного? Понятие идеальной жидкости.
Ответ
Поток – масса движущейся жидкости, направляемая твердыми стенками.

w₁ и w_{2 –} скорости частиц 1 и2.

 Линия тока – линия, в каждой точке которой вектор скорости частицы совпадает с направлением касательной (линия 1-2-3).

Трубка тока – совокупность линий тока, проведенных через все точки контура элементарного живого сечения   .

Элементарная струйка – пучок линий тока, проходящих через трубку тока.

Живое сечение потока – поперечное сечение потока плоскостью, нормальной к направлению скорости жидкости (S).

Смоченный периметр – часть контура живого сечения, по которой поток соприкасается с твердыми стенками (П).

Гидравлический радиус потока R_г – отношение площади живого сечения S к соченному периметру П:

---

 , м.

Эквивалентный диаметр d_э равен учетверенному гидравлическому радиусу:

d_э 

Абсолютная шероховатость стенок ? - это средняя высота выступов неровностей, измеренная в линейных единицах.

Относительная шероховатость   - это отношение абсолютной шероховатости к диаметру трубы:

 .

Расход жидкости – количество жидкости, протекающей через живое сечение потока в единицу времени. Объемный расход измеряется в   , массовый расход в   .

Максимальна около оси трубы, а по мере приближения к стенкам она уменьшается. В расчетах обычно используют среднюю скорость. Средняя скорость движения потока равна отношению объемного расхода к площади живого сечения потока:

 , откуда

объемный расход   ;

массовый расход   .

Скорость жидкости в данной точке – местная (локальная) скорость.



4. Движение жидкости может быть установившимся (стационарным) и неустановившимся (нестационарным).

При нестационарном движении параметры жидкости (давление, скорость) зависят от времени, при стационарном – не зависят.

Напорное движение - поток полностью заполняет поперечное сечение трубы, безнапорное – неполностью.

Равномерное движение – вдоль трубы скорость жидкости постоянна, неравномерное – переменна.

Впервые режимы течения жидкости изучались Рейнольдсом в 1883г.

Режим движения жидкости может быть ламинарным (струйчатым) или турбулентным (вихревым). При ламинарном режиме все частицы

---

жидкости движутся по параллельным траекториям, поперечное перемешивание отсутствует. При турбулентном режиме частицы жидкости движутся по хаотическим траекториям, хотя вся масса жидкости перемещается в одном направлении.

Переход от ламинарного режима к турбулентному происходит тем легче, чем больше массовая скорость жидкости и диаметр трубы и тем меньше вязкость жидкости   .

Критерий Рейнольдса Re:   .

Он является мерой соотношения между силами вязкости и инерции в движущемся потоке.

Переход от ламинарного режима к турбулетному характеризуется критическим значением Re.

Для прямых гладких труб при Re10000 – устойчивый (развитый) турбулентный режим.

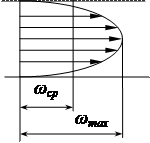
Для ламинарного режима w_ср=0,5w_max, для турбулентного - w_ср=(0,85-0,9)w_max..



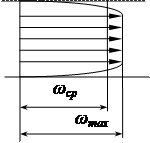
Рис. эпюра скоростей для турбулентного режима.

Непосредственно у самой стенки тербулентного потока имеется ламинарный подслой очень малой толщины δ. В пределах этого слоя происходит резкий рост скорости от нуля на стенке до конечной величины на ее границе. При дальнейшем удалении от стенки происходит переход в турбулентное ядро.

5. При условии недеформируемости и непроницаемости стенок для потока жидкости можно записать (для стационарного режима):

 - уравнение неразрывности (сплошности) потока, или постоянства расхода жидкости.

Для несжимаемой жидкости (ρ=const):

 или   , т.е. средние скорости потока обратно пропорциональны площадям живых сечений.

Уравнение постоянства расхода выражает материальный баланс потока и является частным случаем закона сохранения массы.

Скорость частиц жидкости максимальна около оси трубы, а по мере приближения к стенкам она уменьшается. В расчетах обычно используют среднюю скорость. Средняя скорость движения потока равна отношению объемного расхода к площади живого сечения потока:

---

 , откуда

объемный расход   ;

массовый расход   .

Скорость жидкости в данной точке – местная (локальная) скорость.

2. Приведите вывод уравнения неразрывности для элементарной струйки и для потока жидкости и объясните его физический смысл.
Ответ

Определим уравнения неразрывности потока.



Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

Q1 = υ₁ * F1,

а через сечение 2-2 из него же вытекает объем, равный

Q2 = υ₂ * F2.

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Таким образом

Q1 = Q2

Или

υ₁ * F1 = υ₂ * F2

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Q = υ * F = const.

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

υ₁ / υ₂ = F2 / F1

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.
Решить задачу:

Определить, какое необходимо создать давление с помощью насоса, чтобы лафетный ствол обеспечивал расход равный Q. Потерями напора местными и по длине пренебречь. Диаметр выходного отверстия лафетного ствола d принять по таблице. Схема подсоединения лафетного ствола показана на рисунке 9. Плотность воды 1000 .

---

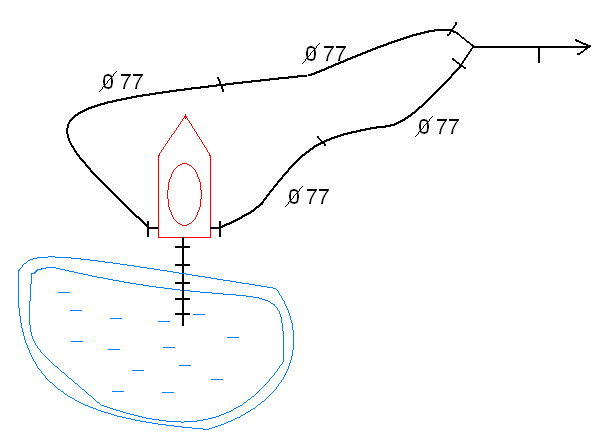
Рис. 9. Рисунок к задаче № 5.

Исходные данные к задаче

d= 28 мм

Q=29 л/с
Решение
Уравнение Бернули:



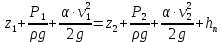
z₁=z₂; P₂=0; α=1

Так как по условию задачи потерями напора по длине можно пренебречь, принимаем h_п = 0.

Таким образом, уравнение примет вид:



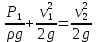
откуда,

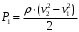
Учитывая, что 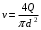, получим

;

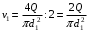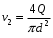
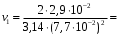3,1 м/с; 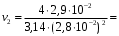47,1 м/с
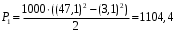Па

Ответ: 1104,4 Па

Задание 6
Ответить на теоретические вопросы:

1. 
   Приведите уравнения движения идеальной и реальной жидкости и поясните, что характеризуют отдельные их члены.
   

Ответ
Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности. В ней отсутствует внутреннее трение, она непрерывна и не имеет структуры.

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 - 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Уравнение стационарного движения, носящее его имя, имеет вид:



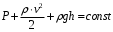
где P - давление жидкости, ρ − её плотность, v - скорость движения, g - ускорение свободного падения, h - высота, на которой находится элемент жидкости.

ρ⋅v²/2 - динамическое давление - кинетическая энергия единицы объёма движущей жидкости;

ρ⋅g⋅h - весовое давление - потенциальная энергия единицы объёма жидкости;

P - статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии ("энергии давления").

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

---

Смотрите также файлы

• Базовые информационные технологии.docx

• Создание рекламной программы для туристических направлений по Нидерландам на примере ооо Олтревел по специальности 43. 02. 10 Туризм.pdf

• Тарау 3в энергия трлері мен кздері 8 орта мектеп кмм кні 02. 2023.docx

• Жоспарды таратуга жане сатуга тыйым салынады!!!! Саба жоспары Бекітемін.docx

• Конспект внеурочного занятия 33 7 класс По страницам Черной книги.docx