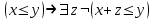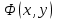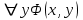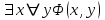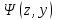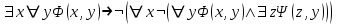Файл: Контрольная работа 1 Задание 1 Построим таблицу истинности для формулы алгебры высказываний и приведём её к сднф и скнф двумя способами.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 28.03.2024

Просмотров: 19

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



Z
→
(
X
∧
Y
)




(
X
→
¬
(
Y
∨
Z
)
)
∨
(
Z
→
(
X
∧
Y
)
)




X
∧
Z




(
X
→
¬
(
Y
∨
Z
)
)
∨
(
Z
→
(
X
∧
Y
)
)
∨
(
X
∧
Z
)




1
1
0
1

0
1
0
1

1
1
0
1

0
1
0
1

1
1
0
1

0
0
1
1

1
1
0
1

1
1
1
1




X
→
Z


X




Z




X
→
Z




0
0
1

0
1
1

1
0
0

1
1
1

Соотношение истинно.

Способ 2

((¬ X ∨ (¬ Y∧ ¬ Z)) ∧ (¬ Z ∨ (X ∧ Y)) ∧ (X ∧ Z)) → (¬X ∨ Z)

(X ∧ (¬ Y∧ ¬Z)) ∨ (Z ∧ (¬ X ∧ ¬ Y)) ∨ (¬X ∨ ¬Z) ∨ (¬X ∨ Z)

X ∧¬ Y ∨ ¬ X∧¬ Z ∨ Z∧¬ X ∨ Z ∧ ¬ Y ∨ (¬X ∨ ¬Z) ∨ (¬X ∨ Z)

X ∧¬ Y ∨ ¬ X∧¬ Z∨ Z∧¬ X ∨ Z ∧ ¬ Y ∨ ¬ X

X ∧¬ Y ∨ ¬ X∧¬ Z∨ Z ∧ ¬ Y ∨ ¬ X

X ∧¬ Y ∨ Z ∧ ¬ Y∨ ¬ X ∧ Z

X
Y
Z
¬ Y
X ∧¬ Y
Z ∧ ¬ Y
X ∧¬ Y ∨ Z ∧ ¬ Y
¬ X
¬ X ∧ Z
X ∧¬ Y ∨ Z ∧ ¬ Y∨ ¬ X ∧ Z

0
0
0
1
0
0
0
1
0
0

0
0
1
1
0
1
1
1
1
1

0
1
0
0
0
0
0
1
0
0

0
1
1
0
0
0
0
1
1
1

1
0
0
1
1
0
1
0
0
1

1
0
1
1
1
1
1
0
0
1

1
1
0
0
0
0
0
0
0
0

1
1
1
0
0
0
0
0
0
0

Из таблицы видно, что данное выражение не является тавтологией, а значит, соотношение не является верным

Способ 3

¬ (((¬ X ∨ Y ∨ Z) ∧ (¬ Z ∨ (X ∧ Y)) ∧ (X ∧ Z) → ¬ (¬X ∨ Z))

(¬ X ∨ Y ∨ Z) ∧ (¬ Z ∨ (X ∧ Y)) ∧ (X ∧ Z) ∧ (¬X ∨ Z)

(¬ X ∨ Y ∨ Z) ∧ (¬ Z ∨ X) ∧ (¬ Z ∨ Y) ∧ (X ∧ Z) ∧ (¬X ∨ Z)

  1. ¬ X ∨ Y ∨ Z

  2. ¬ Z ∨ X

  3. ¬ Z ∨ Y

  4. X

  5. Z

  6. ¬X ∨ Z

  7. [6,7] 0

Получили пустую резольвенту, значит, отношение верно
Задание 3

Построим вывод для следующей формулы ИВ:

   ⊢ ( )

1) (гипотеза);

2) ;

  1. ;

  2. ;




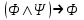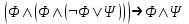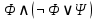
Задание 4

???? = Z;−, X = {7,21};

Любое число, получаемое из чисел 7, 21 с помощью операции вычитания четное, то ????(X)=2

Контрольная работа №2

Задание 1

Выпишем подформулы заданной формулы:

  1. (x  y) → z (x + z  y)











y - связанная, x - свободная переменные

Поскольку существуют связанные и свободные вхождения переменных х, y в формулу, то х, y являются связанными и свободными переменными. Переменная z связанная.

  1. xy(x, y)→ (x (y(x, y)  z(z, y)))





















Поскольку все вхождения переменных x, y, z связанные, то переменные x,y,z связанные.

Задание 2

Множество истинности предиката , это 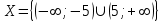, следовательно, множество истинности предиката это .

Проверим справедливость отношения . Так как множество истинности предиката , это 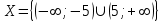, отсюда следует справедливость .

Проверим справедливость отношения . Так как множество истинности предиката , это , отсюда не следует справедливость

а) Высказывание 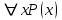является истинным, так как множество истинности предиката , это 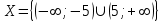, следовательно, указанный интервал полностью содержится в нём.

б) Высказывание 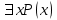является истинным, так как множество истинности предиката , это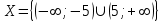 , следовательно, указанный интервал содержит значение х=6, которое справедливо для предиката .

Задание 3

Составим программу реализующую машину Тьюринга, вычисляющую значение функции: ????(????, ????) = 5???? ∸ 3????

Смотрите также файлы