Некоторые теоремы разрешимости нелинейных уравнений второго рода и их приложения к уравнениям с сингулярными интегралами

Х.Б. Ханикалов

ДГУ, Махачкала

УДК 517.946

Аннотация: В статье исследуются нелинейные уравнения второго рода с сингулярными интегралами в комплексных пространствах 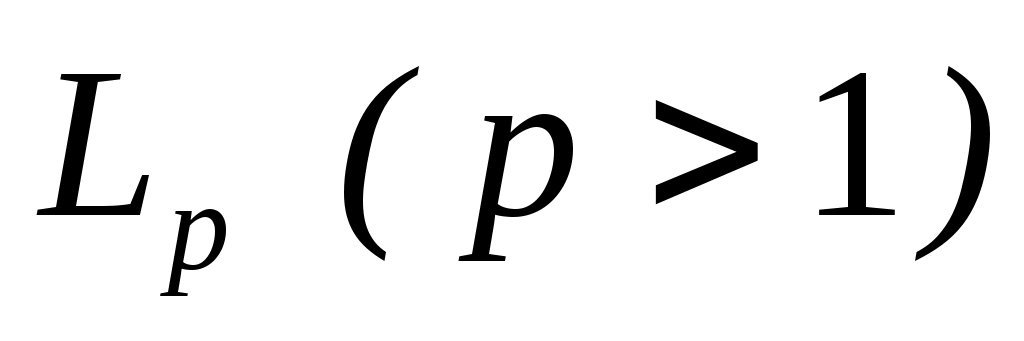. Приведены теоремы разрешимости этих уравнений.

Ключевые слова: оператор, монотонность, коэрцитивность, нелокальная
разрешимость, пространства.
Рассматриваются общие уравнения и системы типа





в действительных и комплексных пространствах .

Всюду в работе - линейный вектор-оператор, вектор - оператор - известный оператор суперпозиции, называемый оператором Немыцкого, - в общем случае вектор-функция.

В наших приложениях А – линейный сингулярный интегральный оператор и он не может быть компактным и не действует в L₁. Мы нигде в работе от Fu не требуем малоконструктивного для систем условия монотонной (секторной) ограниченности оператора F.

Полученные общие результаты для уравнений (I) и (II) перенесены на случай когда А – линейный сингулярный интегральный оператор, а оператор F действует из L_p в L_q. Частично результаты анонсированы ранее в работах [5]- [7].
1. Общие теоремы существования и единственности
Всюду в работе ,

,

- гладкая линия на комплексной плоскости С. Функция

---

С С измерима на контуре при каждом C и непрерывна по при каждом .

Функция называется монотонной по почти при каждом , если

.

Всюду в работе - монотонная функция в комплексном С.

Теорема 1.1. Пусть функция удовлетворяет неравенству

(1)

линейный оператор ограниченный и положительный.

Тогда при каждом уравнение (I) имеет решение в . Если, кроме того, хотя бы один из операторов А или F строго монотонен, то это решение единственное в .

Доказательство. Если в уравнении (I) сделать замену на а вместо написать , то у нас получится уравнение в котором

---

, а вместо будет В дальнейшем и будем считать такими.

Рассмотрим вспомогательное уравнение



где - оператор сопряжённый A, n - натуральное число. Оператор , очевидно, непрерывный и монотонный. Из коэрцитивности первого слагаемого и положительности остальных двух операторов следует коэрцитивность оператора при каждом фиксированном n. Поэтому уравнение имеет решение (см.[4]). Из положительности каждого слагаемого в Ф_n следует, что



т.е. что последовательность равномерно ограничена числом . Интегрируя обе части в , получим

.

Из условия (1) имеем

.

Из последнего с учётом и , получим ограниченность последовательности Умножая обе части

---

на , получим



Отсюда следует равномерная ограниченность последовательности Из последнего следует, что



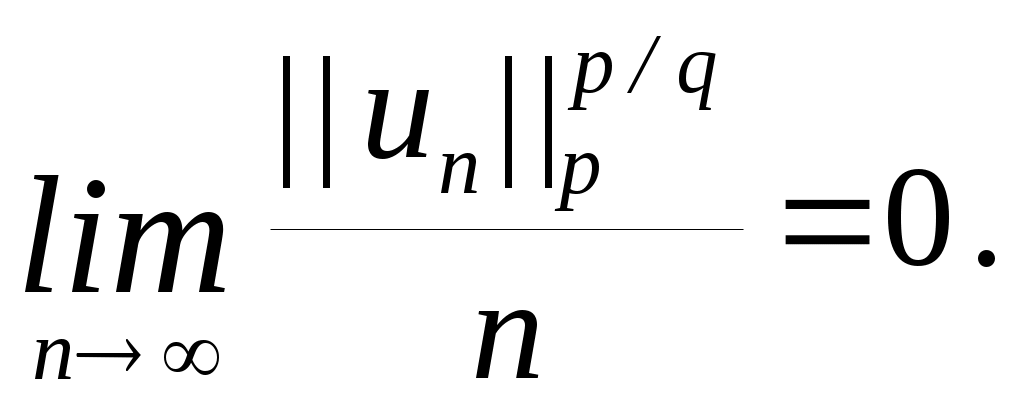
Из ограниченности следует существование слабо сходящейся к подпоследовательности

Монотонность оператора



и сильная сходимость в к нулю первого слагаемого в дает слабую

сходимость к .

Из монотонности следует, что существует для которой верно



почти всюду, т. е. является решением уравнения (I).

Единственность решения вытекает непосредственно из уравнения (I).

Пусть и – разные решения уравнения. Тогда получим



Умножая обе части последнего равенства на выражение в скобках и интегрируя с мерой , получим

---

Если строго монотонный, то из первого равенства следует

Если оператор строго монотонный, то и уже из уравнения (I) следует

Следствие 1.1. Если оператор в теореме ограничен в и - решение уравнения (I) из , то Это следует из того, что

Следствие 1.2. Если в неравенстве (1) нет , т.e. , то при любом измеримом уравнение имеет решение такое, что

Это следует из того, что

Замечание 1.1. В теореме ограничение является в целом необходимым. Мы построили пример линейного оператора и монотонного



при которых уравнение (I) заведомо не имеет решения.

Пусть


где

---

Смотрите также файлы

• По профилю специальности пм. 01. Организация мероприятий, направленных на укрепление здоровья ребенка и его физического развития.docx

• Первообразная.docx

• Задержание последа.doc

• Контрольная работа по дисциплине Антикризисное управление Вариант 5 Обучающийся группы 9574 Закирова А. Р.docx

• Тепловая электрическая станция (тэс).docx