Файл: Некоторые теоремы разрешимости нелинейных уравнений второго рода и их приложения к уравнениям с сингулярными интегралами.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- единичная окружность с центром в точке (0,0). В следующем пункте 2 доказывается, что  – положительный оператор.
– положительный оператор.
На единичной окружности функцию из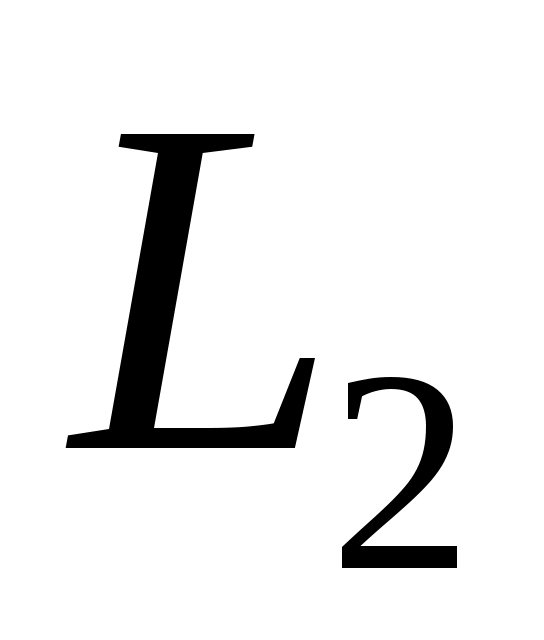
 всегда можно разложить в ряд
всегда можно разложить в ряд
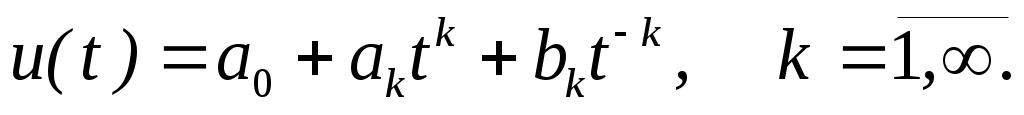
Но если подставить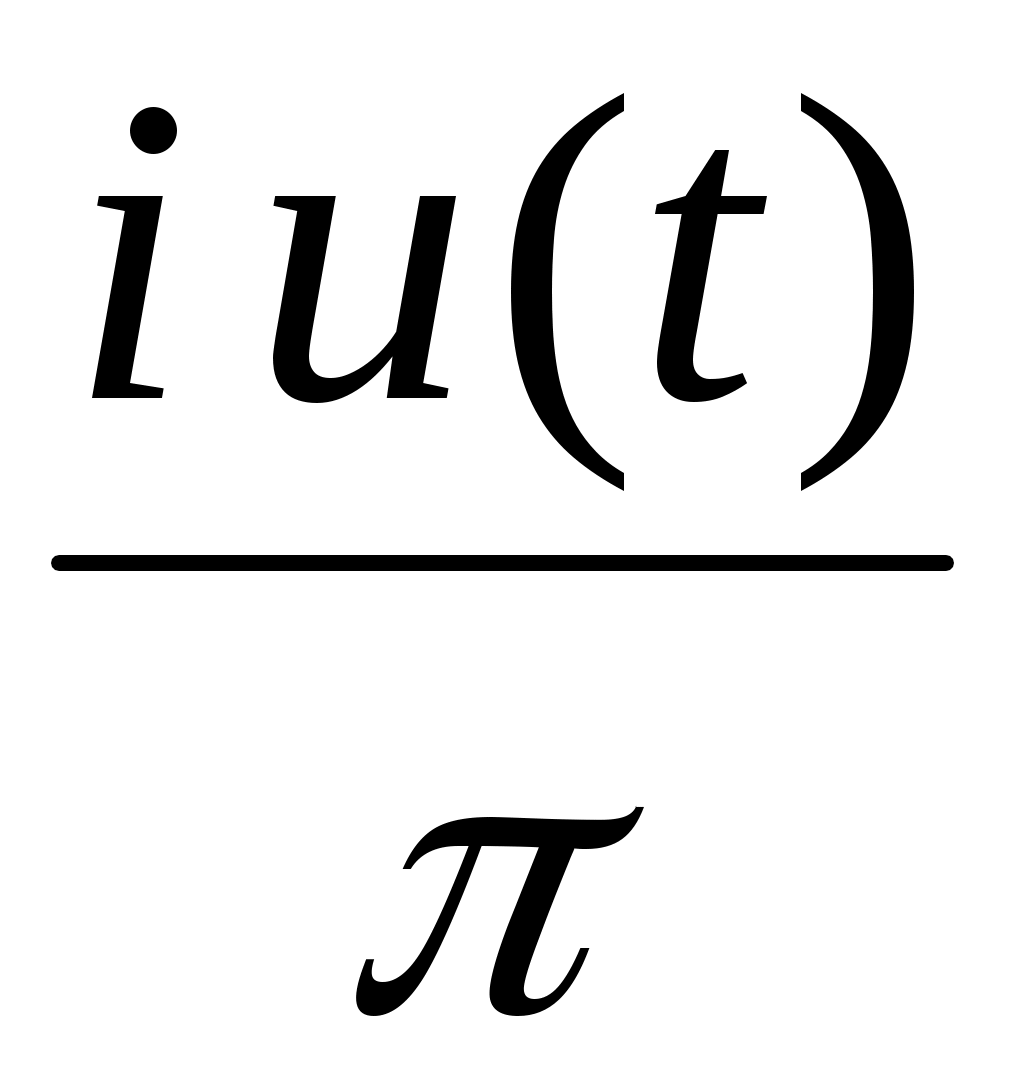 в оператор
в оператор  , мы получим
, мы получим
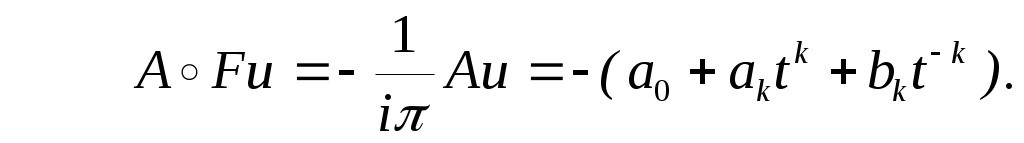
Значит
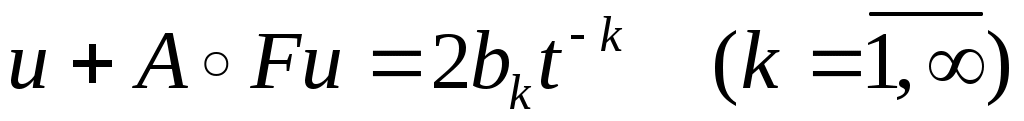
для любых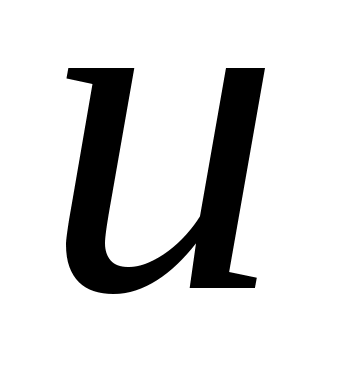 из
из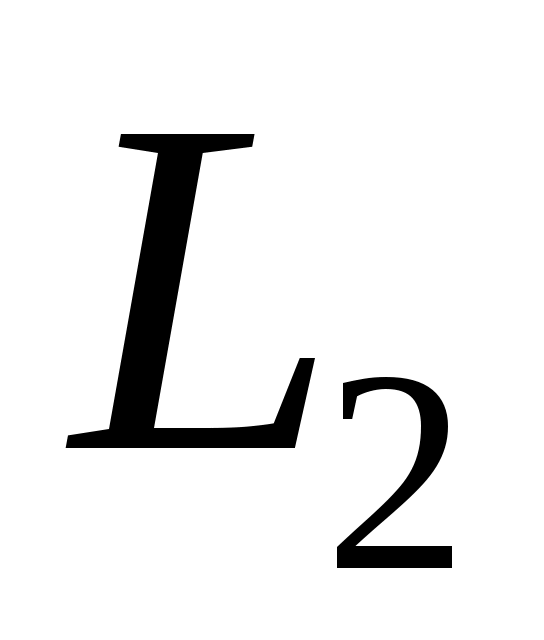 . Если в правой части взять
. Если в правой части взять 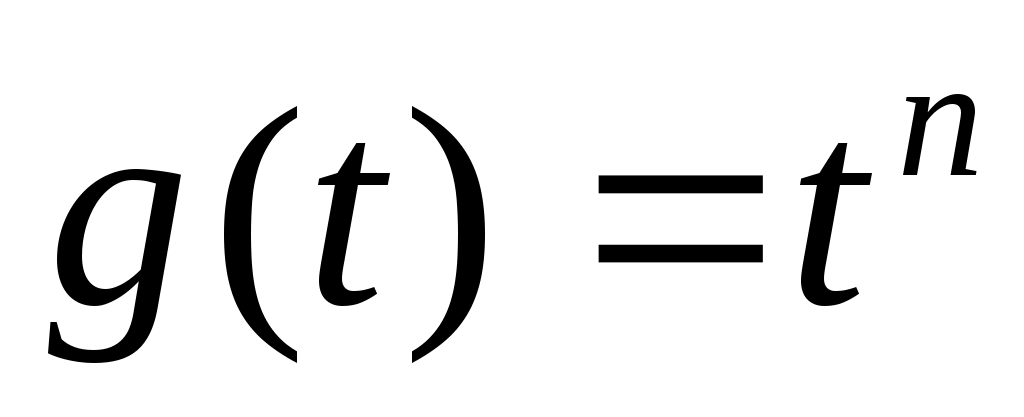 при любом натуральном
при любом натуральном  , то уравнение (I) не имеет решения ни в каком известном пространстве.
, то уравнение (I) не имеет решения ни в каком известном пространстве.
Этот пример говорит и о необходимости существенных дополнительных ограничений на операторы или
или 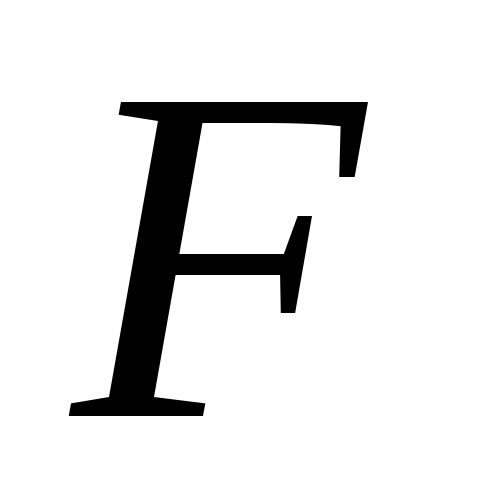 при доказательстве гипотетического утверждения теоремы 3 работы [1].
при доказательстве гипотетического утверждения теоремы 3 работы [1].
Эти авторы так и поступили при доказательстве соответствующих утверждений в работах [3], [4].
Рассмотрим теперь уравнение (II).
Теорема 1.2. Пусть оператор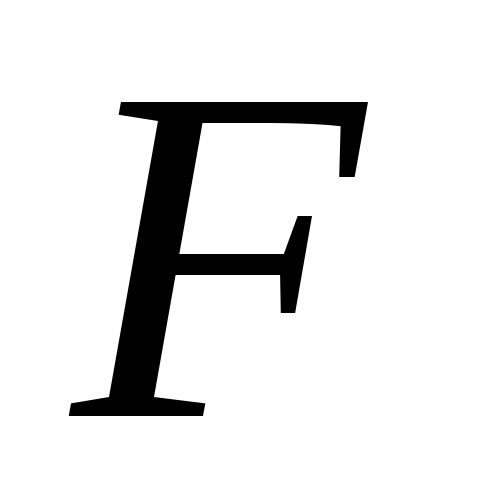 удовлетворяет условиям предыдущей теоремы, оператор
удовлетворяет условиям предыдущей теоремы, оператор  - линейный ограниченный в любом
- линейный ограниченный в любом 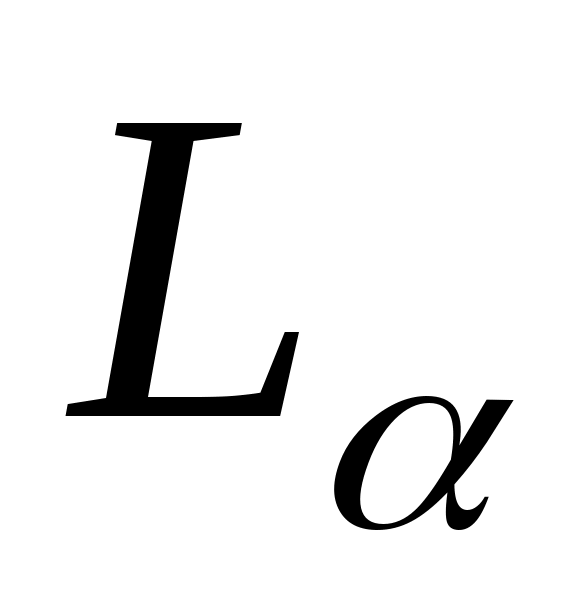 , положительный, кроме того
, положительный, кроме того

Тогда уравнение (II) имеет решение в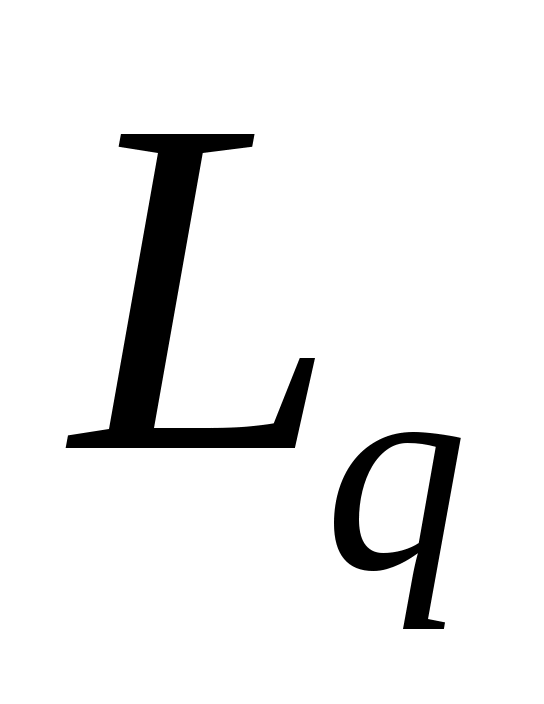
.
Если, кроме того, хотя бы один из операторов или
или 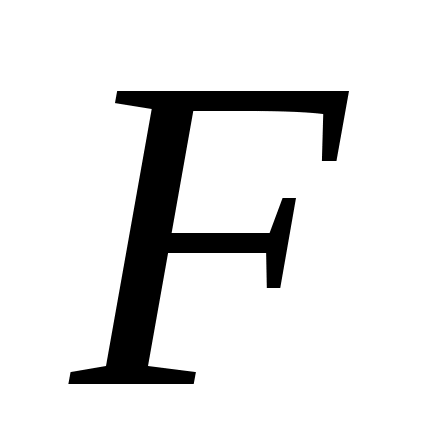 строго монотонен, то это решение единственное в
строго монотонен, то это решение единственное в 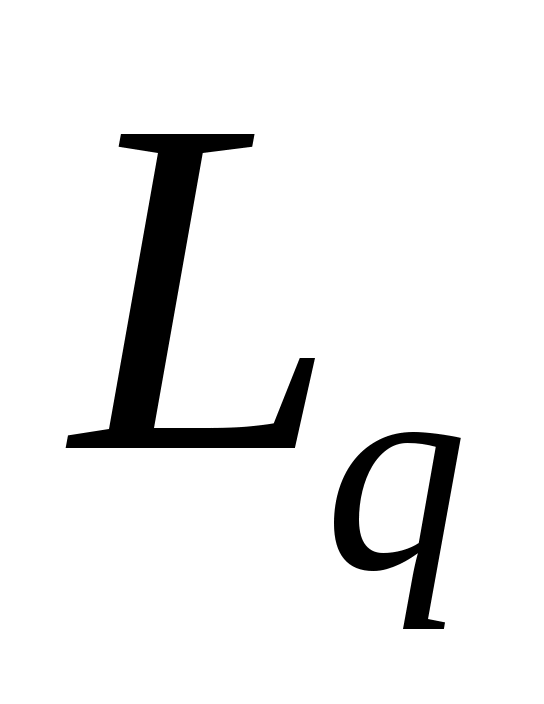 .
.
Для доказательства строятся уравнения
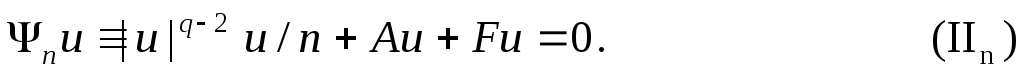
Первое и третье слагаемые действуют из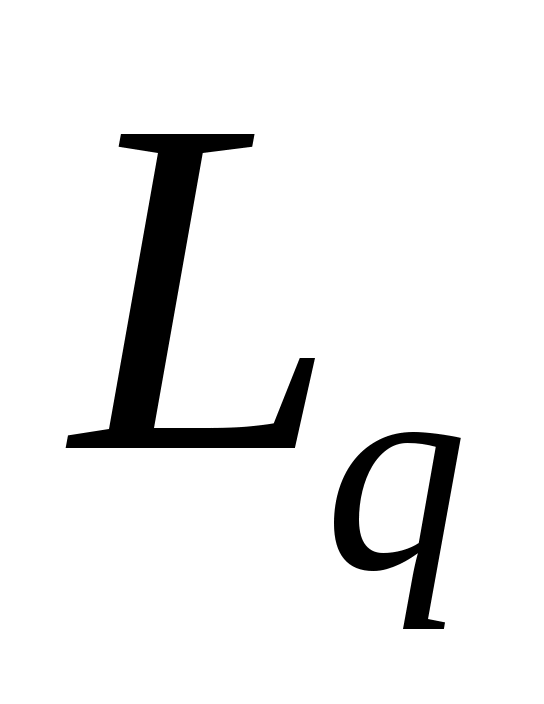 в
в 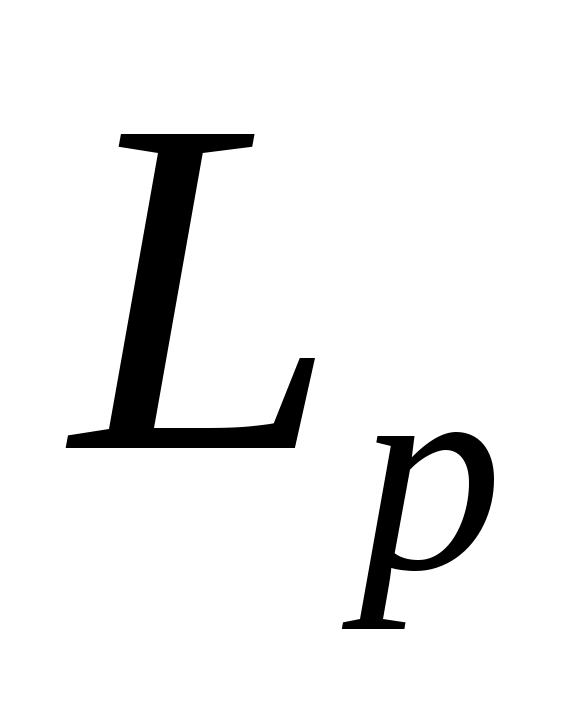
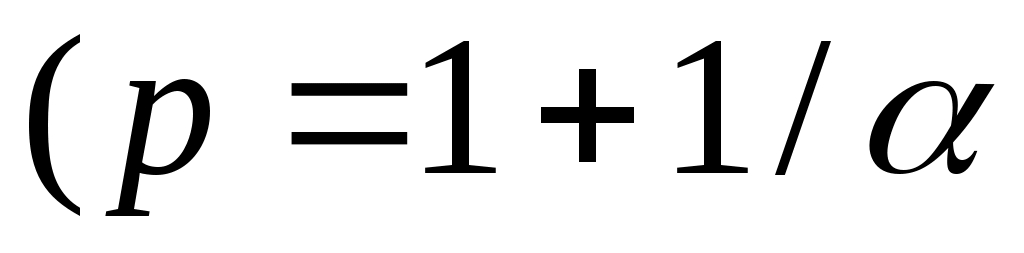 ,
, 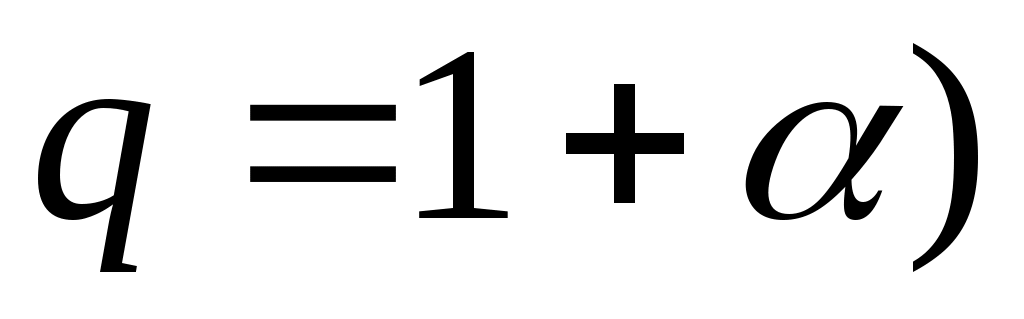 , являются непрерывными множествами, и их сумма является коэрцитивной в
, являются непрерывными множествами, и их сумма является коэрцитивной в 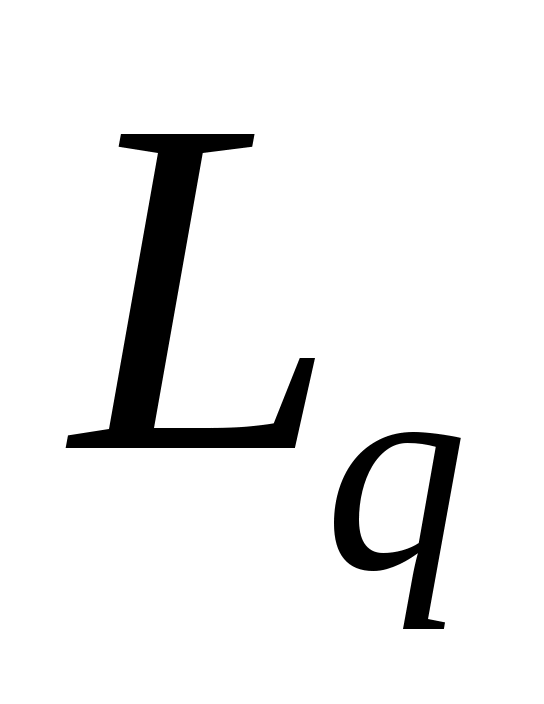 . Оператор
. Оператор  положительный в том смысле, что
положительный в том смысле, что 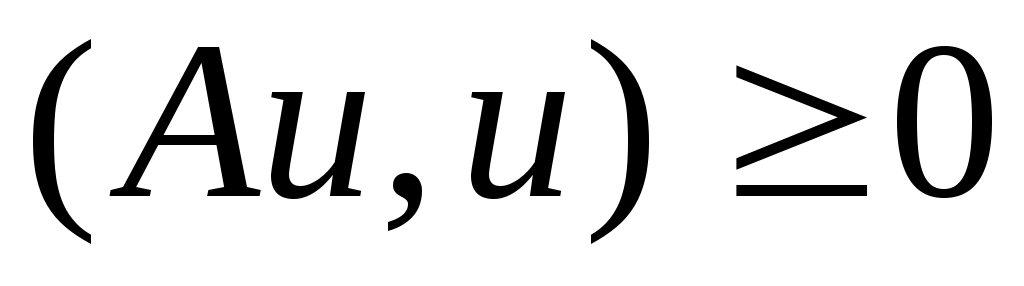 при любом
при любом 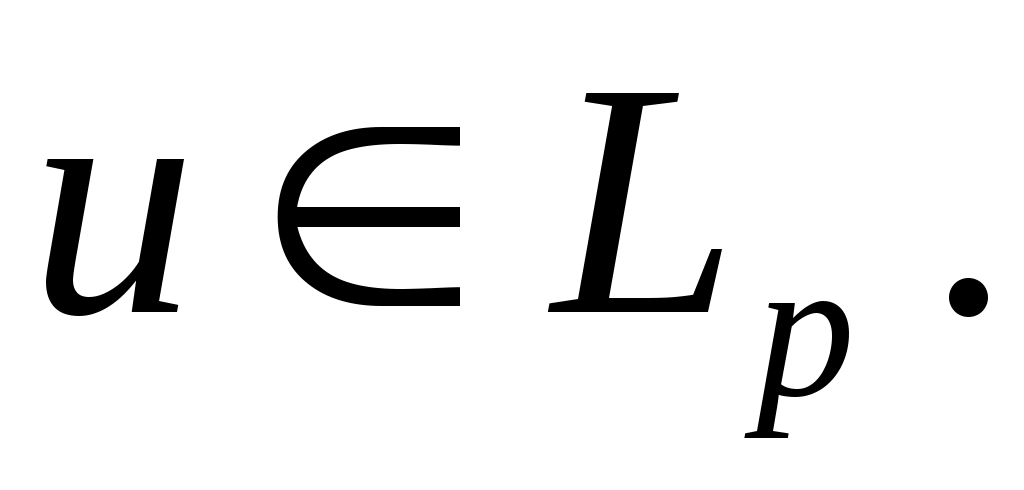
Берем общий для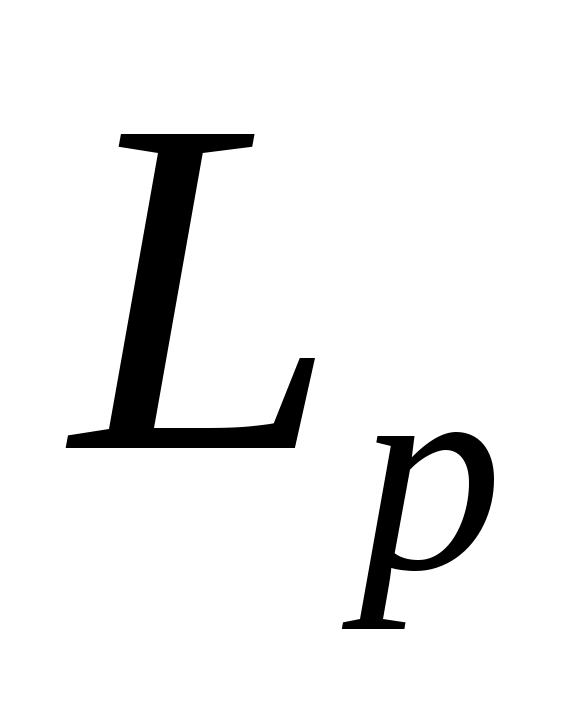 и
и 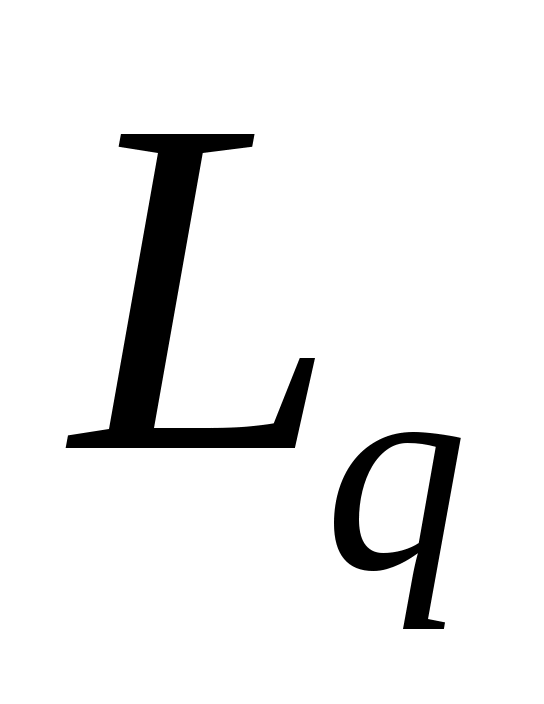 базис
базис 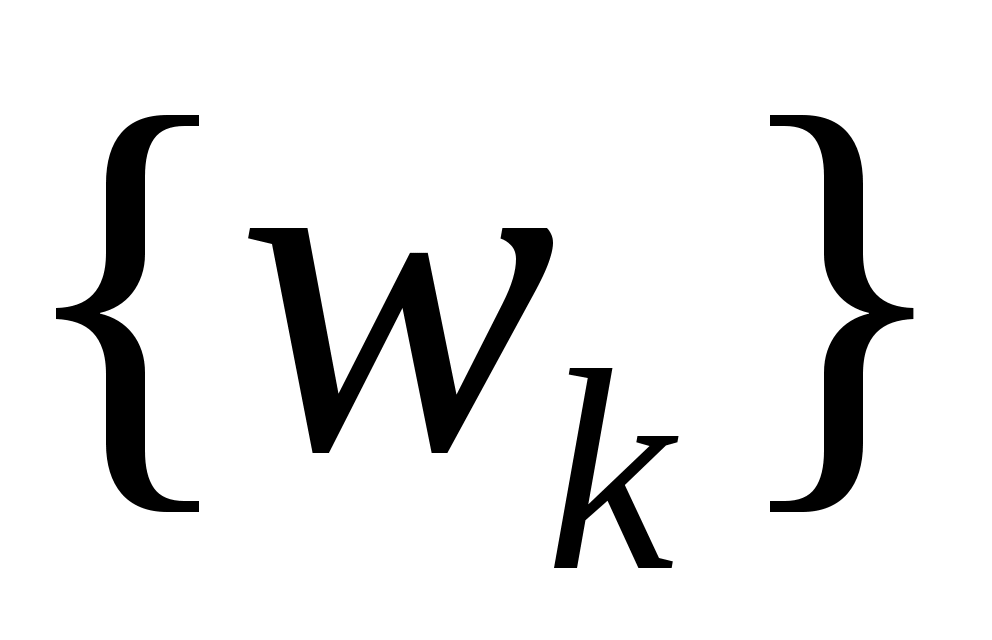 и составим подпространства из многочленов
и составим подпространства из многочленов 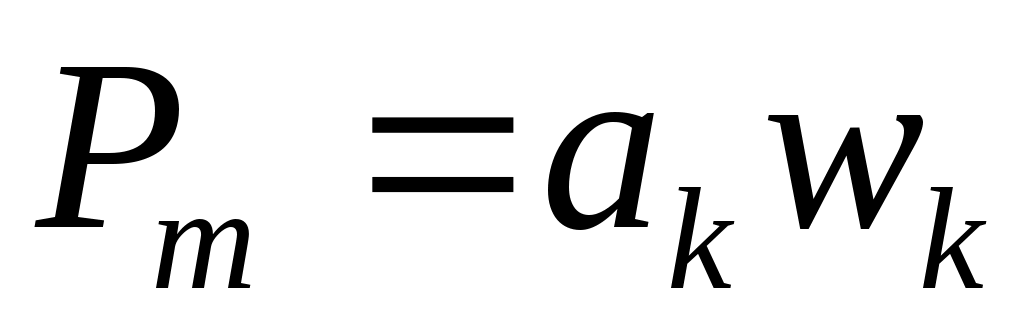 ,
, 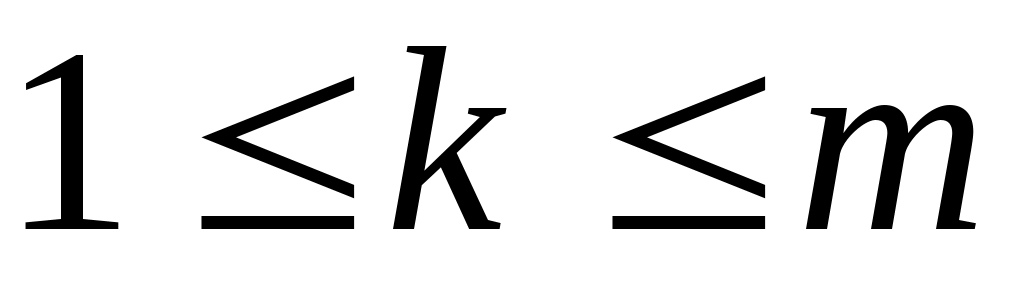 . В этих подпространствах нормы эквивалентны и оператор
. В этих подпространствах нормы эквивалентны и оператор 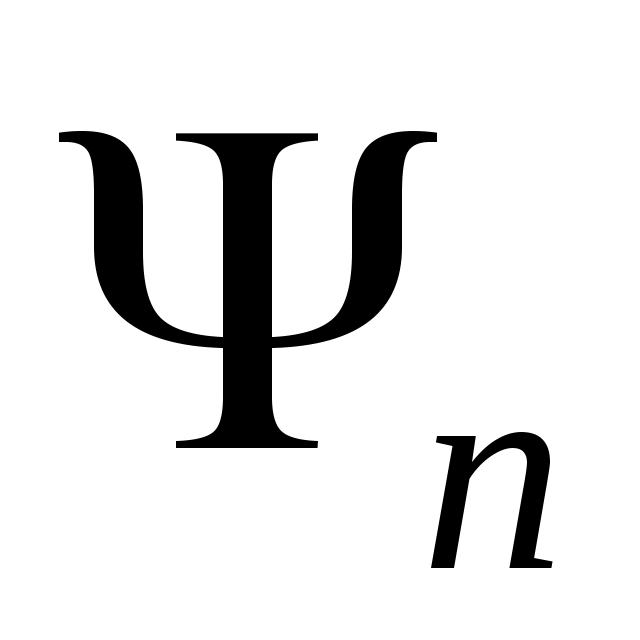 коэрцитивный как оператор из
коэрцитивный как оператор из 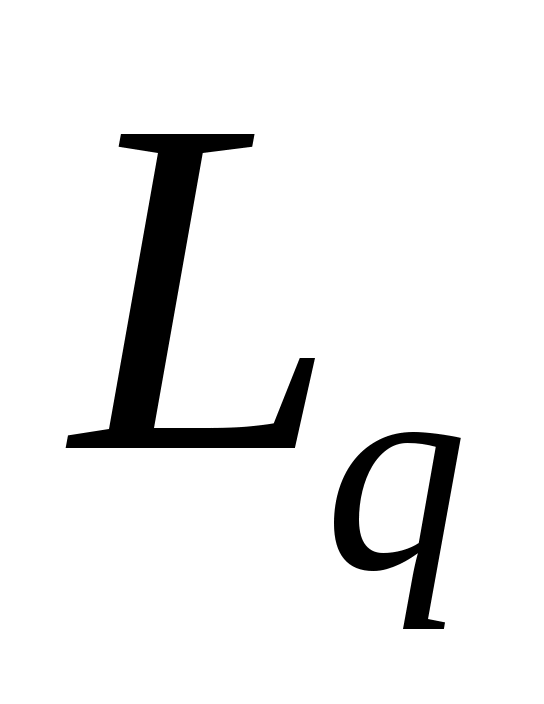 в
в 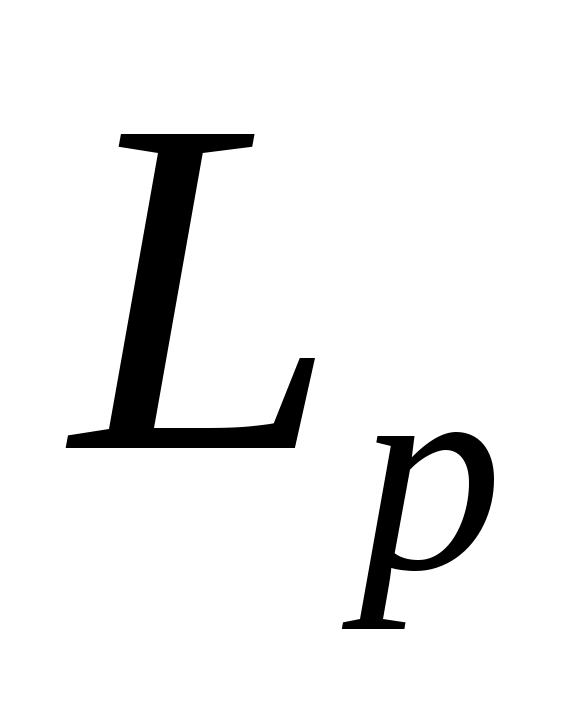 . Значит уравнение
. Значит уравнение 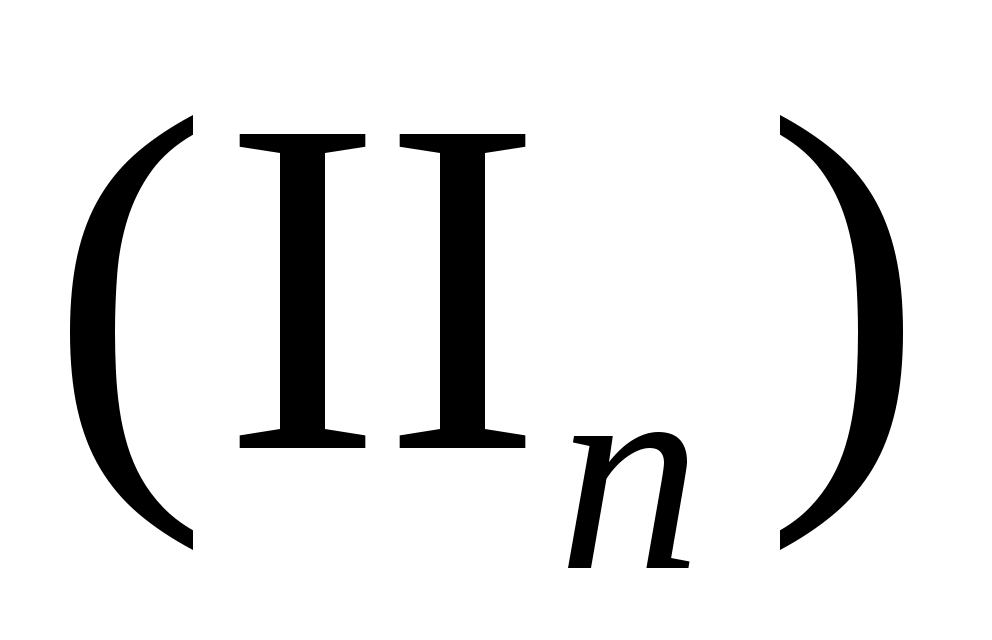 имеет решение
имеет решение 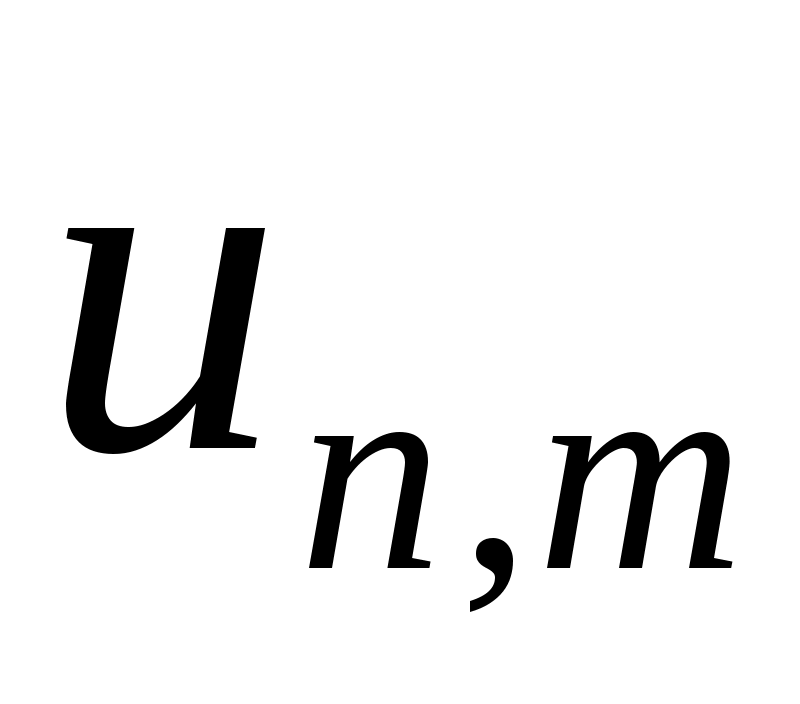 в каждом
в каждом 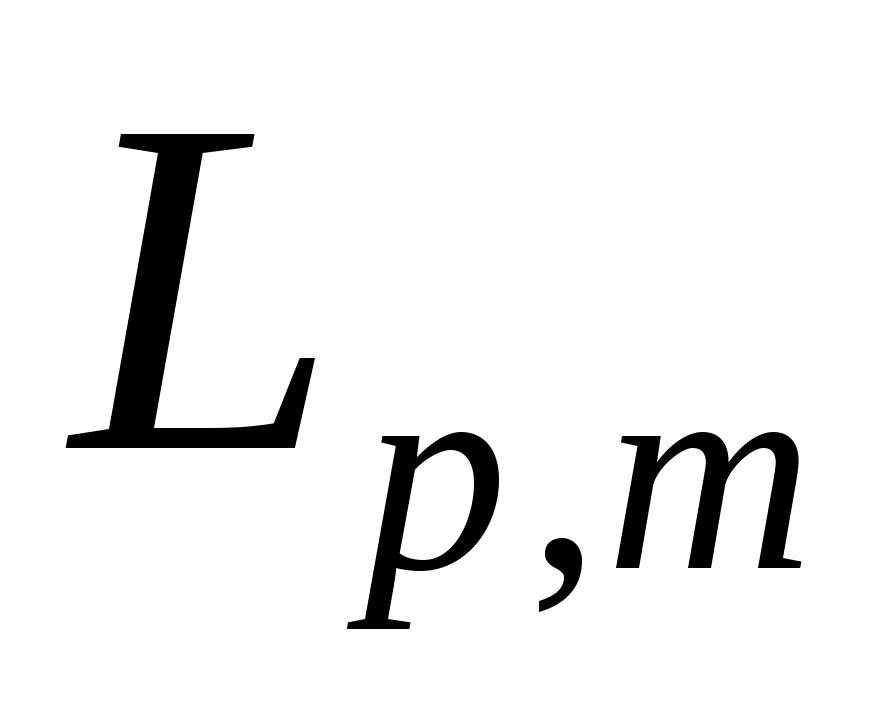
, имеющий такой смысл, что

Из коэрцитивности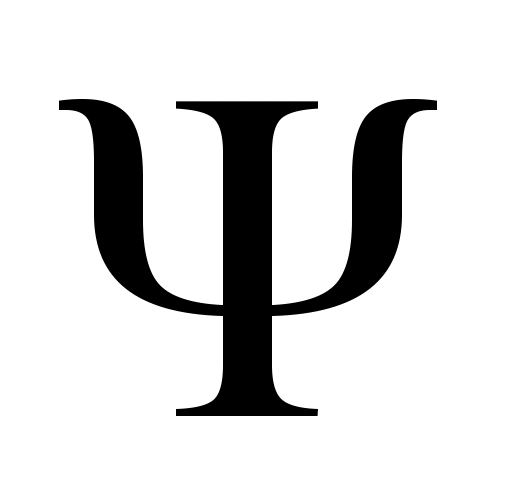 следует равномерная ограниченность множества
следует равномерная ограниченность множества  в
в 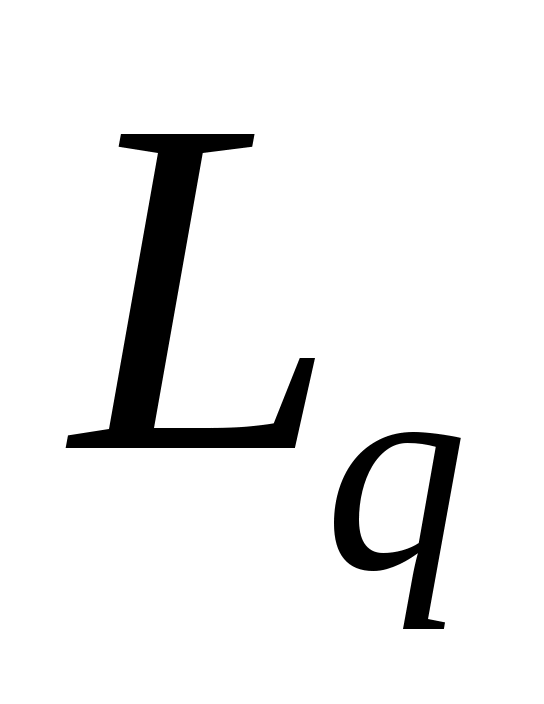 . Используя монотонность
. Используя монотонность 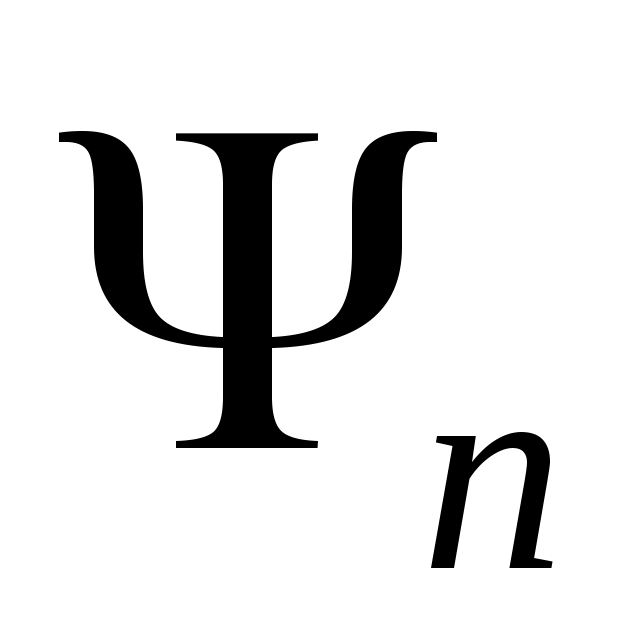 мы получим существование слабого предела
мы получим существование слабого предела 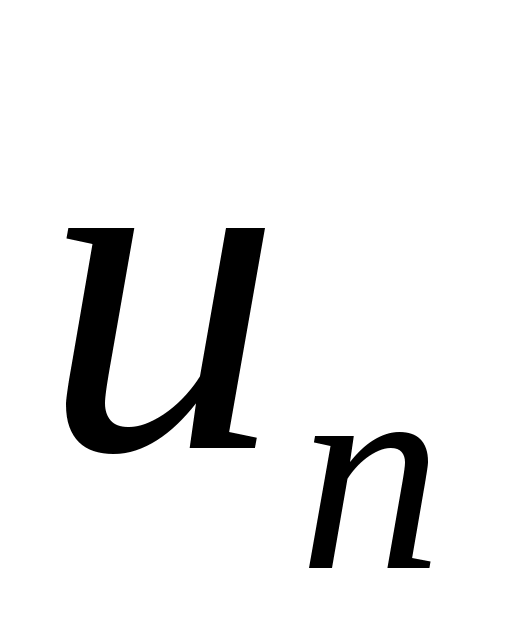 подпоследовательности из
подпоследовательности из 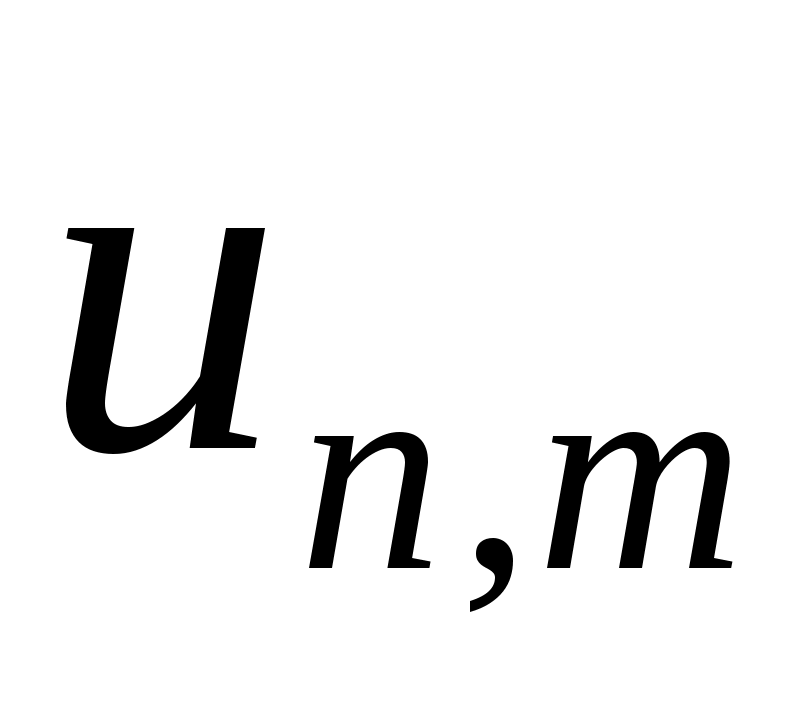 , которая является решением
, которая является решением 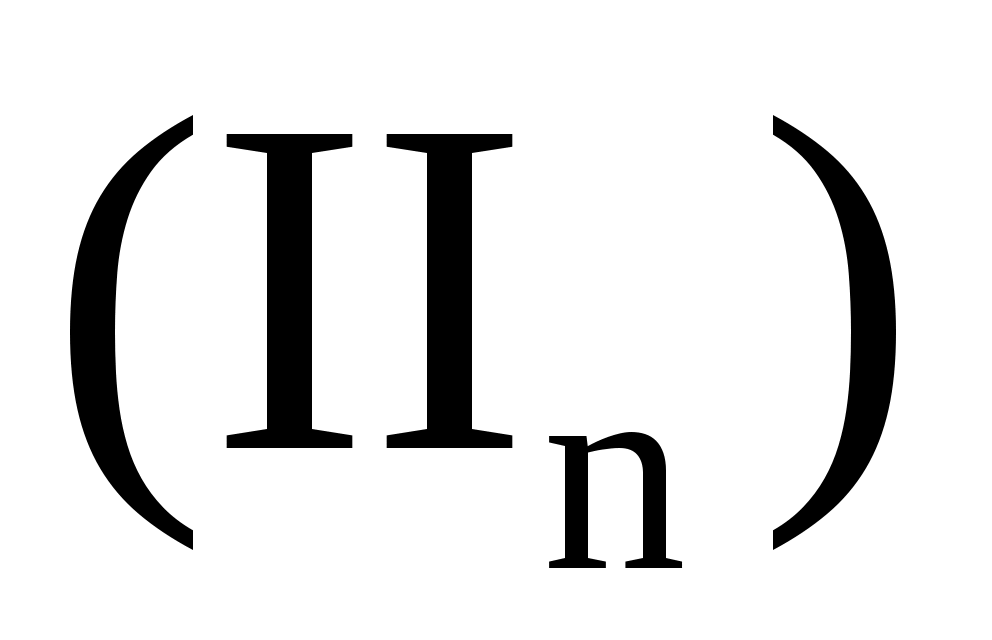 . Но поскольку первое и третье слагаемые в
. Но поскольку первое и третье слагаемые в 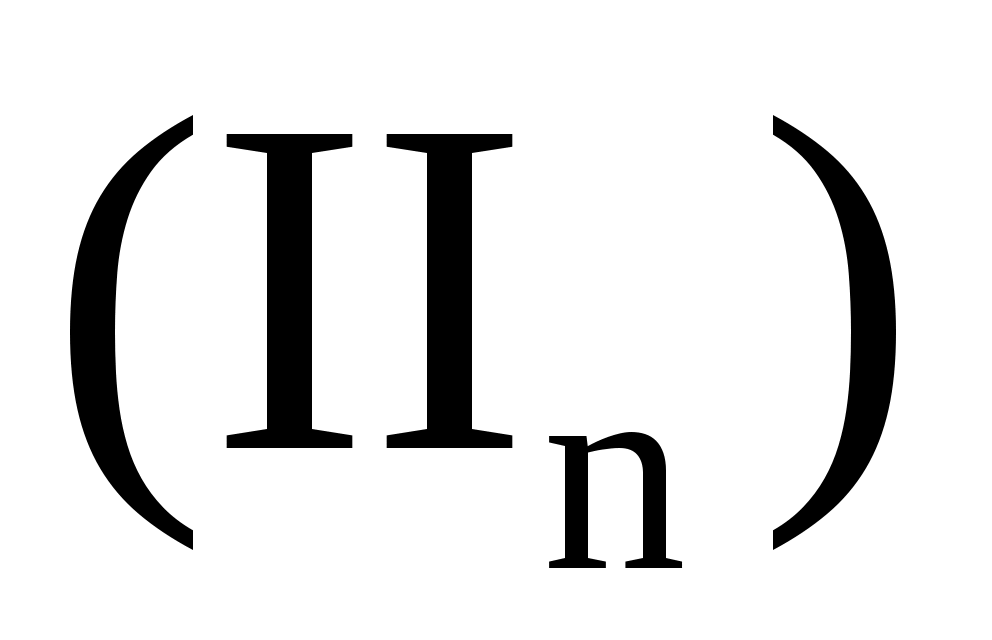 принадлежат
принадлежат  , то и
, то и 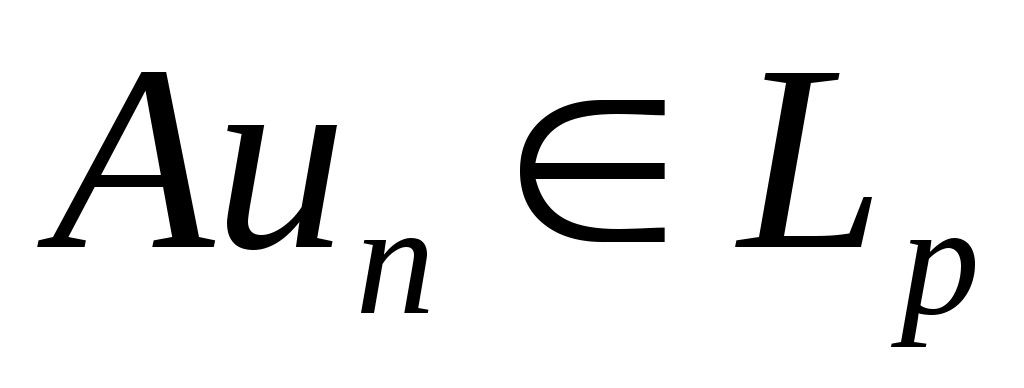 .
.
Из тождества и положительности
и положительности  следует ограниченность множества
следует ограниченность множества 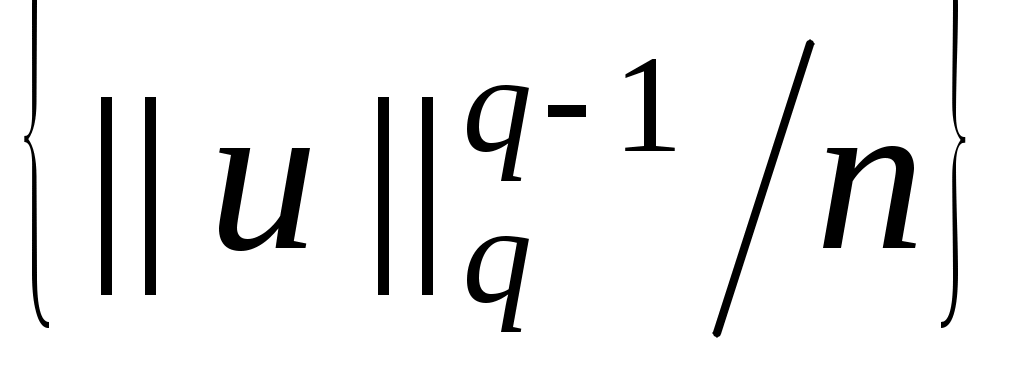 числом
числом 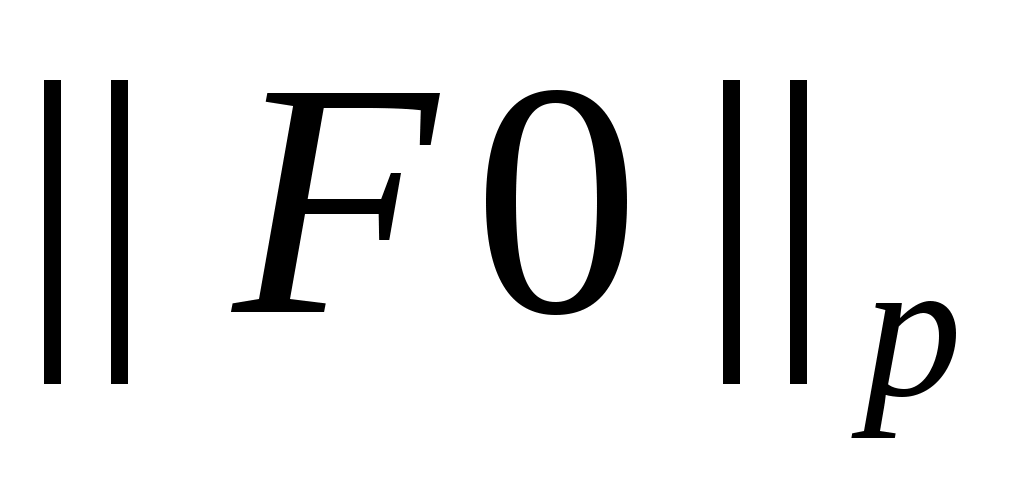 .
.
Используя условия (1) и (2) получается

С учетом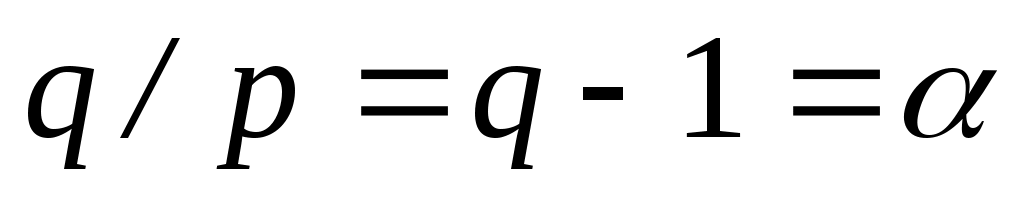 , ограниченности первого слагаемого в неравенстве,
, ограниченности первого слагаемого в неравенстве, 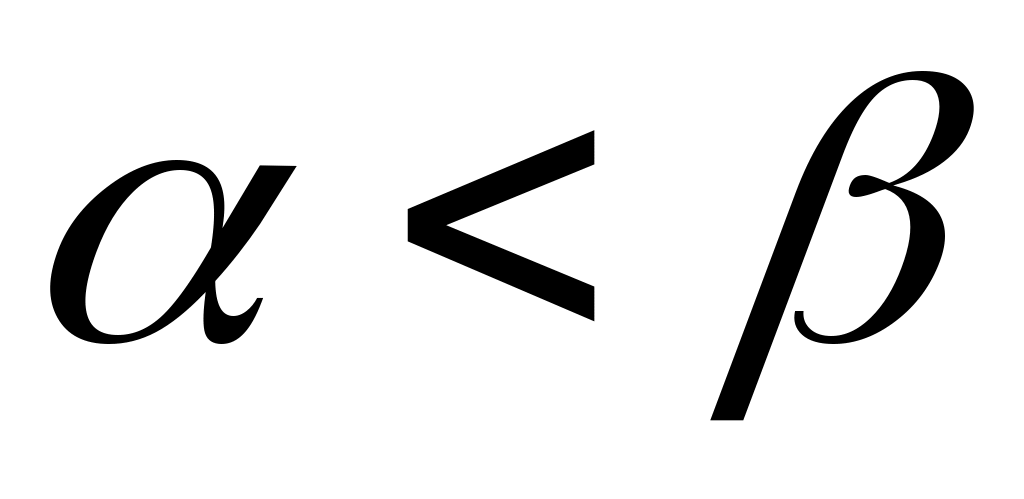 , мы получаем равномерную ограниченность
, мы получаем равномерную ограниченность 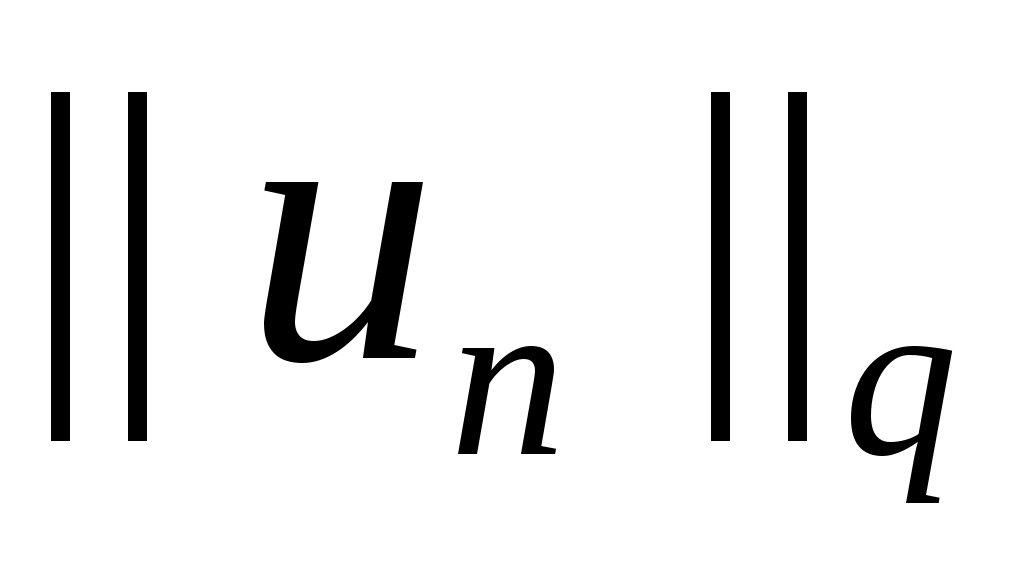 . Значит из
. Значит из  можно выделить подпоследовательность
можно выделить подпоследовательность 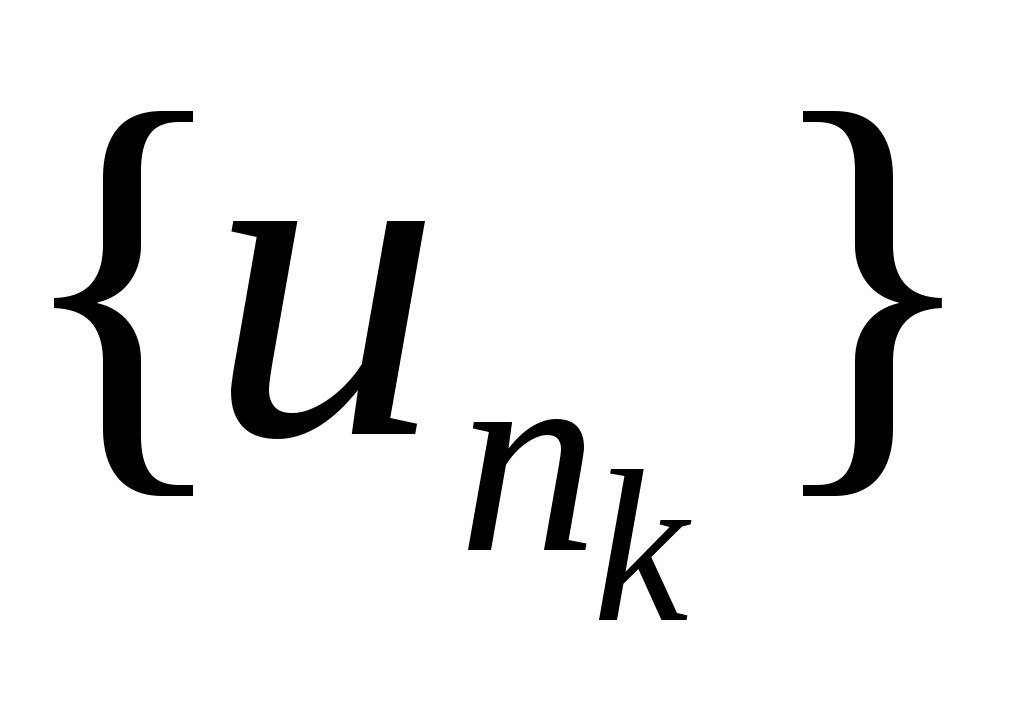 такую, что
такую, что 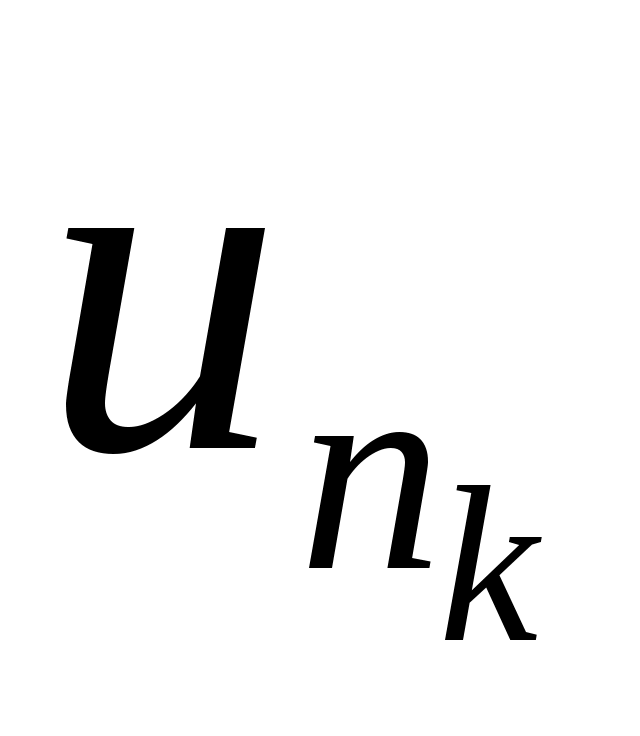
, ,
, 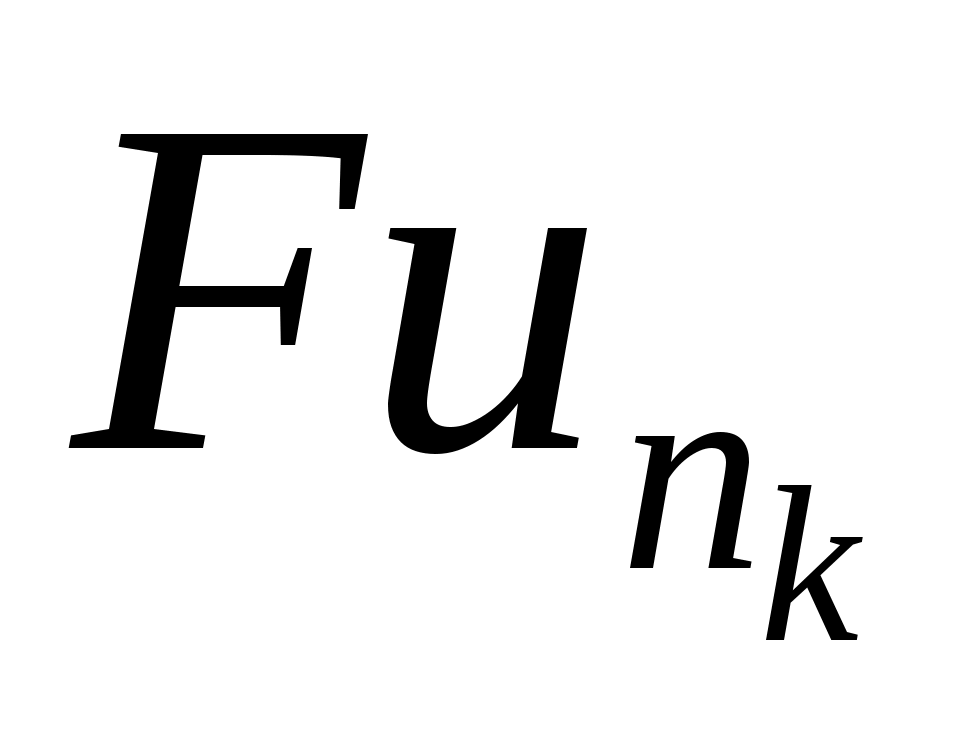 сходятся слабо к
сходятся слабо к 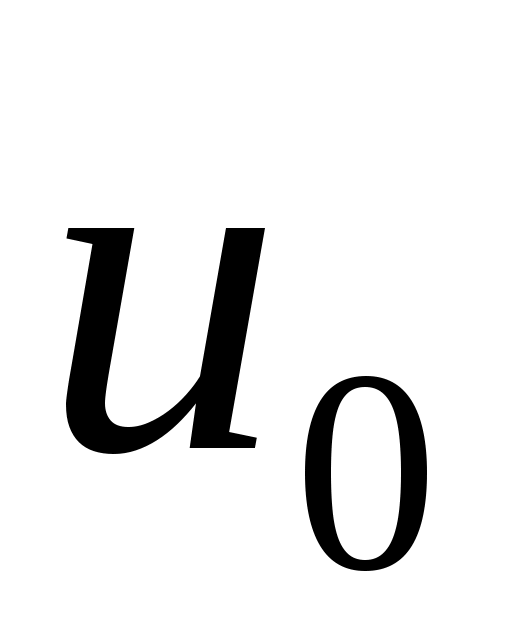 ,
, 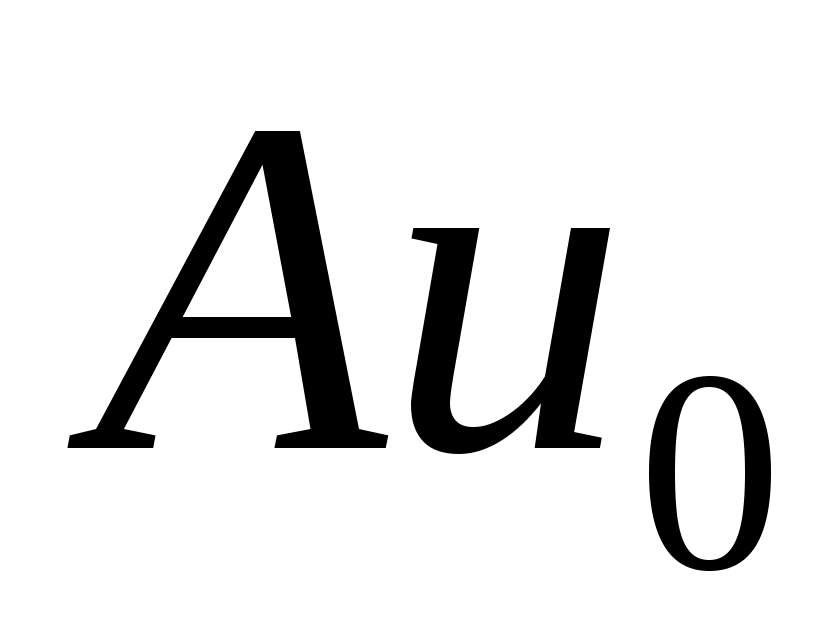 ,
, 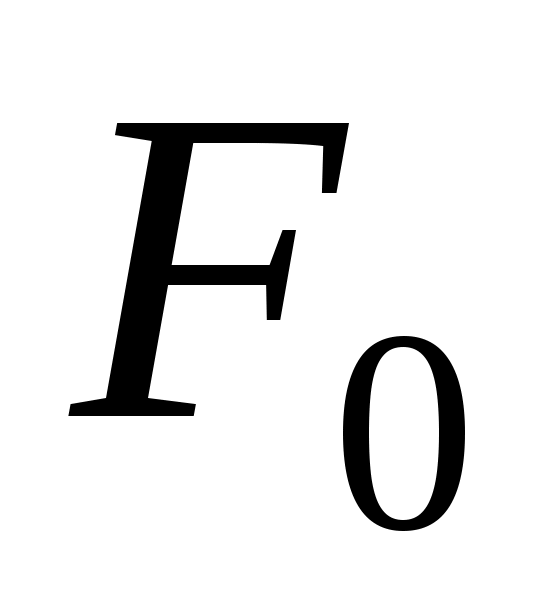 соответственно. Первое слагаемое в
соответственно. Первое слагаемое в 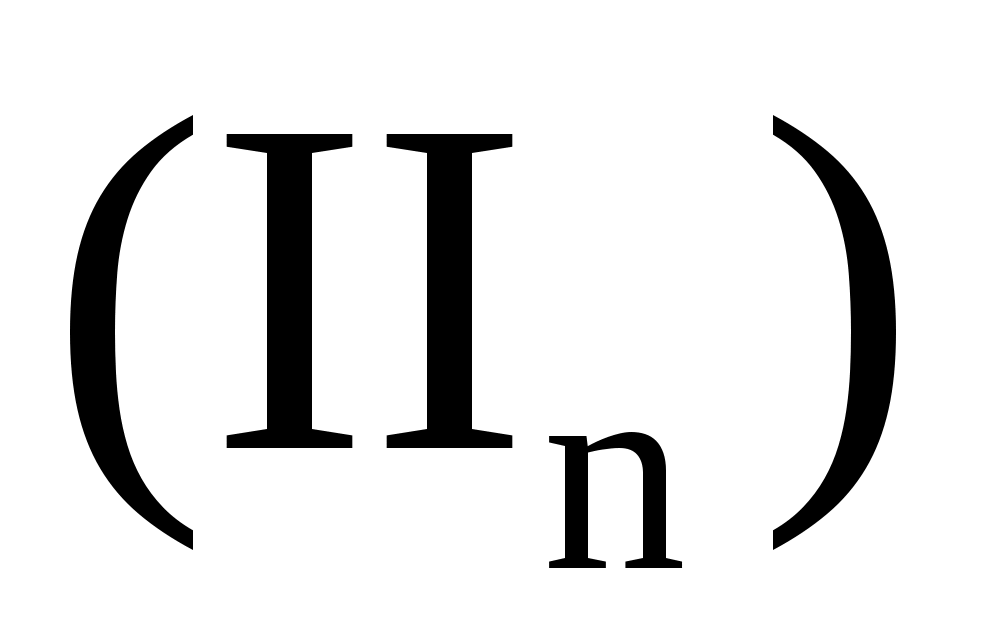 сходится к нулю по норме в
сходится к нулю по норме в  . Пользуясь монотонностью
. Пользуясь монотонностью 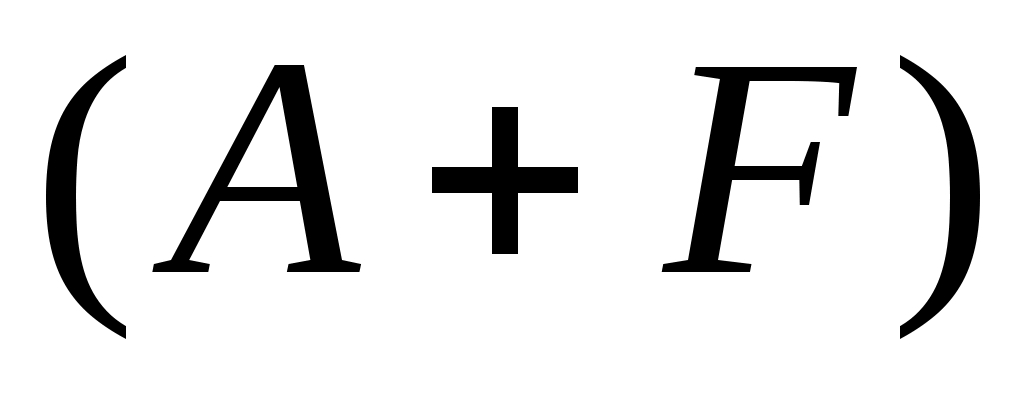 , мы получим
, мы получим 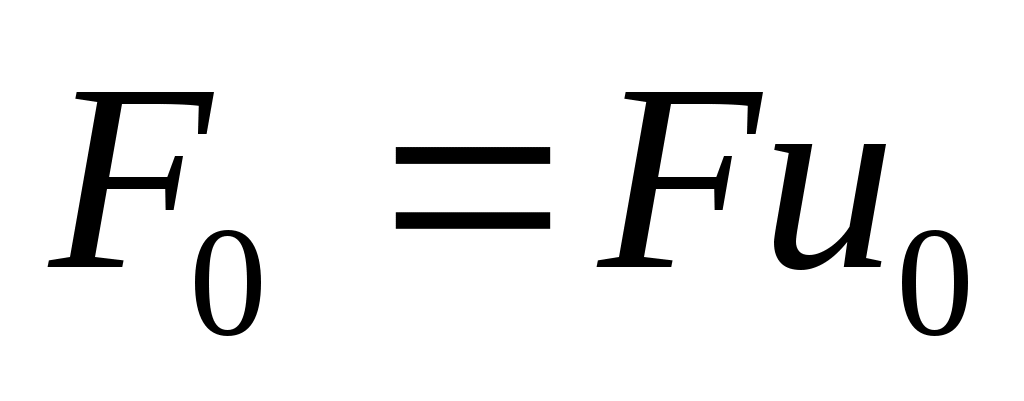 , причем,
, причем, 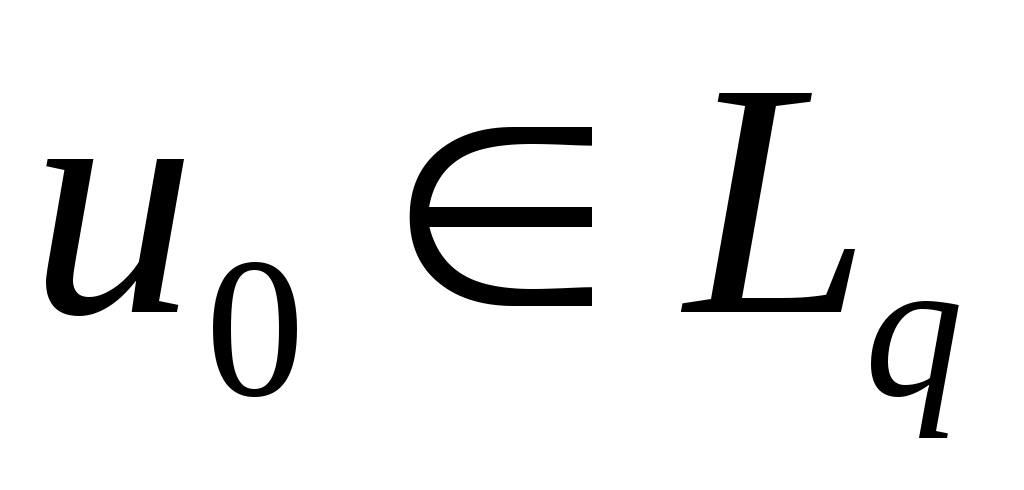 ,
, 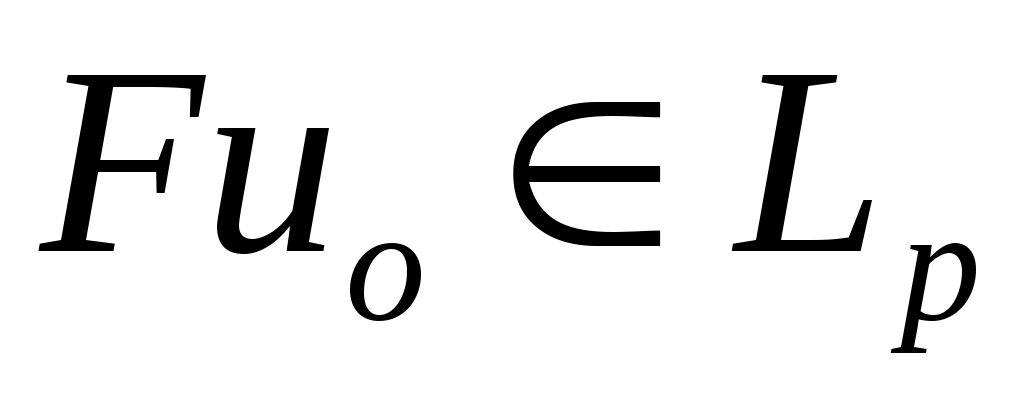 . Значит,
. Значит, 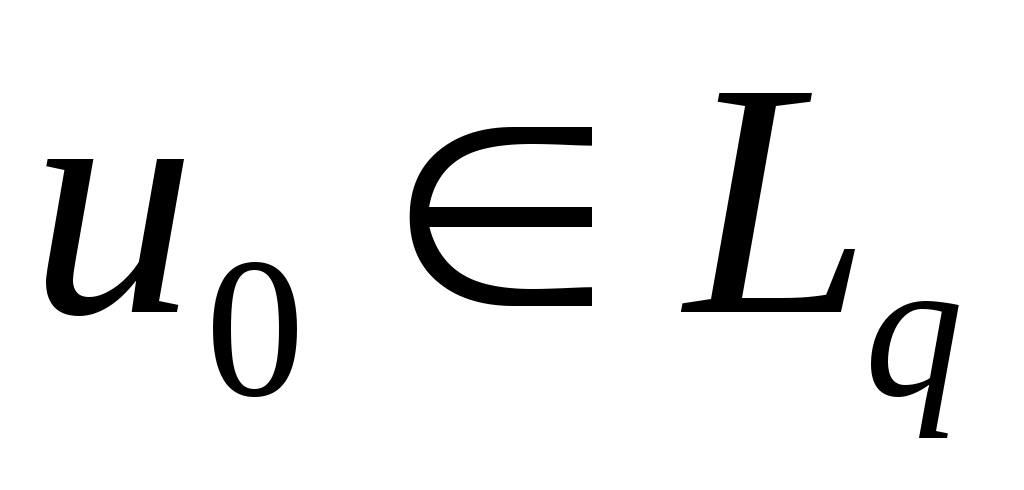 является решением уравнения (II).
является решением уравнения (II).
Единственность решения доказывается как в предыдущей теореме.
Замечание 1.2. Если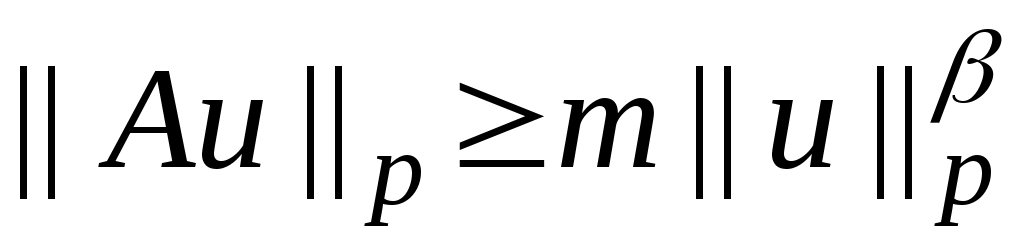 , то решение уравнения существует в
, то решение уравнения существует в  при тех же условиях теоремы 2.
при тех же условиях теоремы 2.
Теорема 1.3. Пусть функция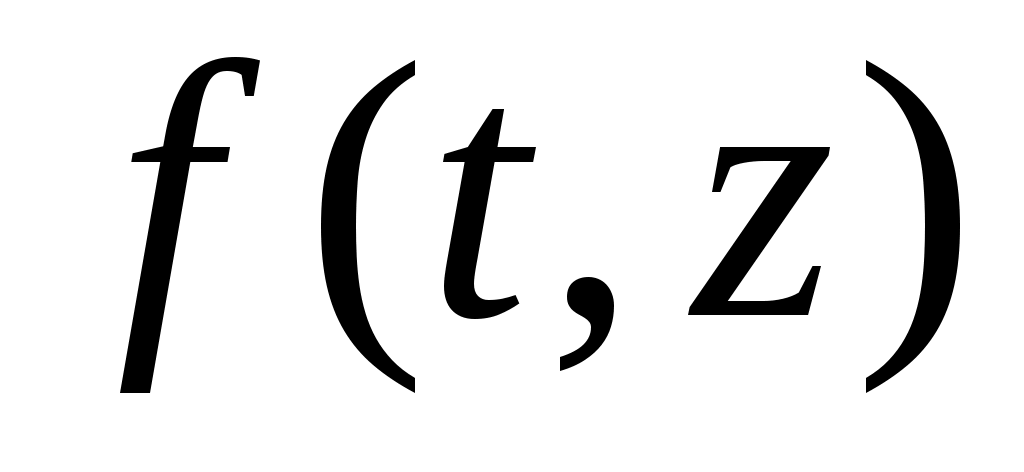 удовлетворяет неравенствам
удовлетворяет неравенствам

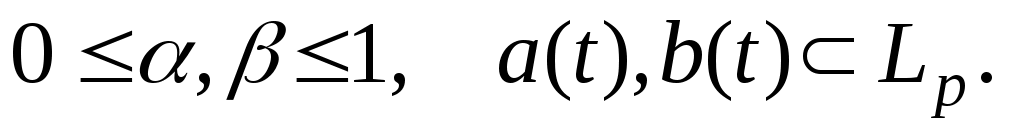
Пусть далее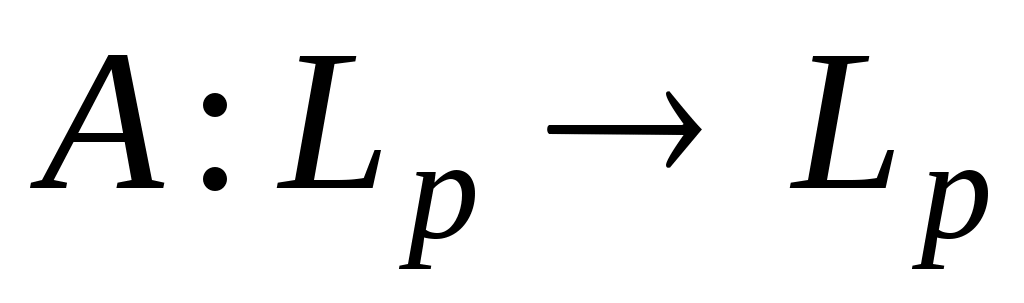 – линейный непрерывный и положительный оператор при
– линейный непрерывный и положительный оператор при 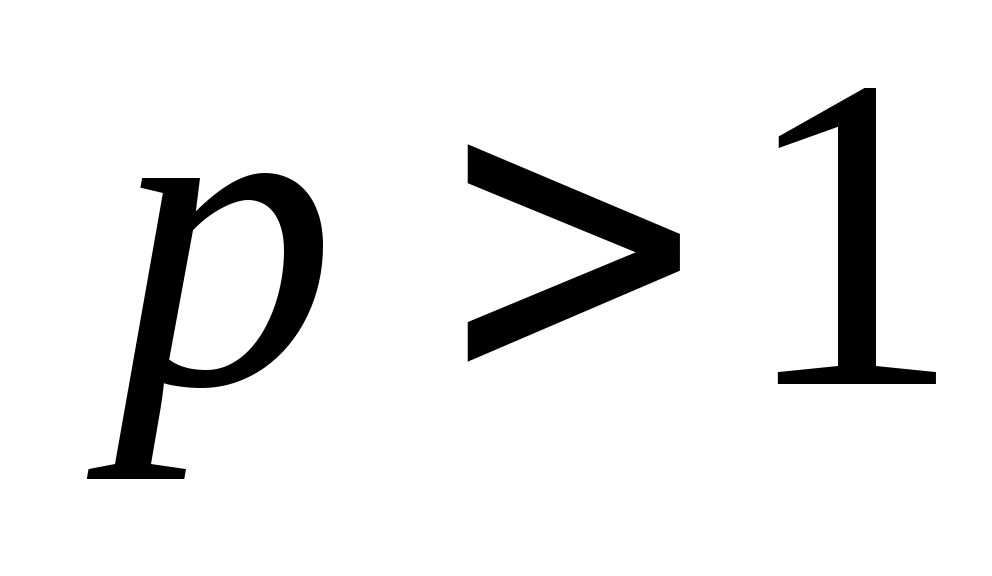 . Тогда уравнение (II) имеет решение в
. Тогда уравнение (II) имеет решение в 
 .
.
Доказательство. В случае оператор
оператор 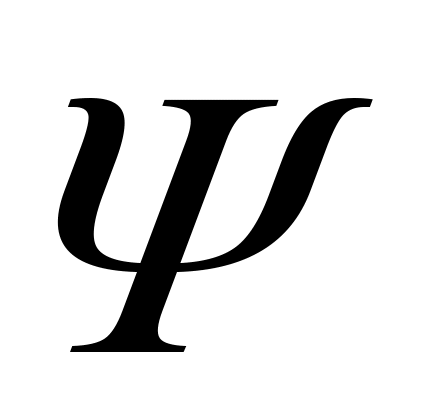
непрерывный, монотонный в , а из левой части (3) следует его коэрцитивность в
, а из левой части (3) следует его коэрцитивность в  . Значит, уравнение имеет решение в
. Значит, уравнение имеет решение в  .
.
При строим такую “срезку”
строим такую “срезку”  функции
функции  , чтобы
, чтобы
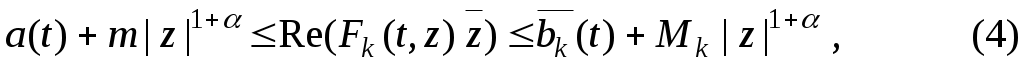
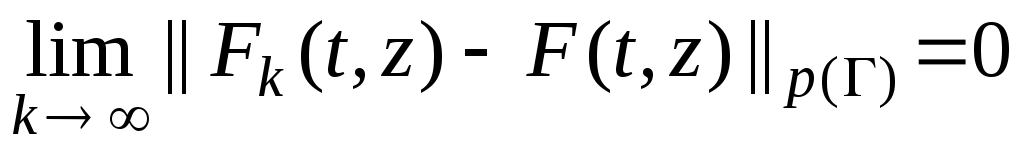
с сохранением монотонности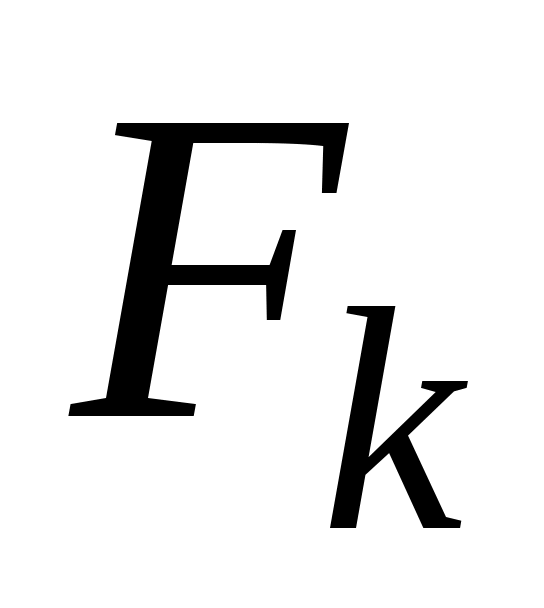 по
по  . Возможность такого построения
. Возможность такого построения  геометрически очевидна. В достаточно большом круге
геометрически очевидна. В достаточно большом круге 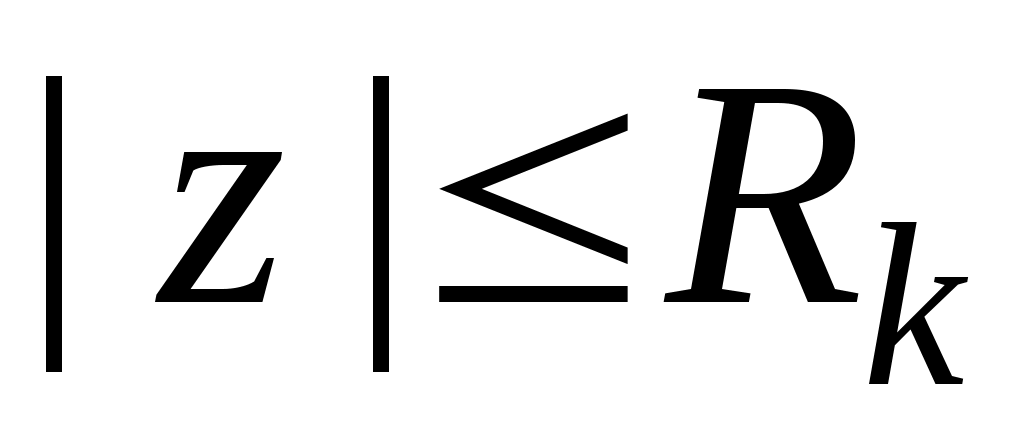 функции
функции 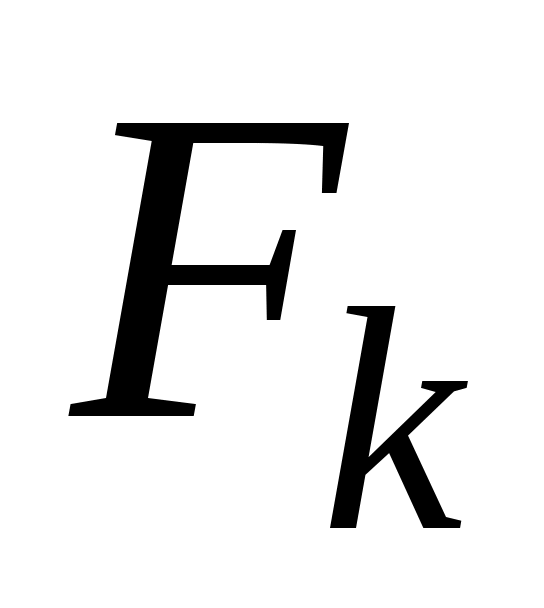 и
и 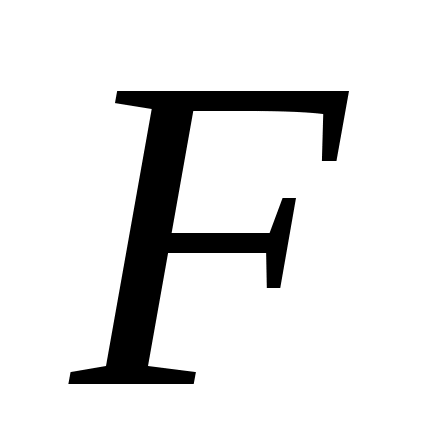 совпадают, а дальше строятся
совпадают, а дальше строятся 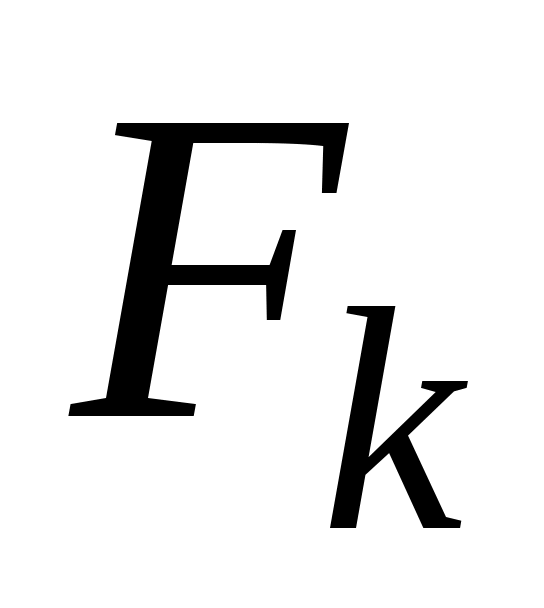 так, чтобы сохранить непрерывность и монотонность по z, конечно
так, чтобы сохранить непрерывность и монотонность по z, конечно 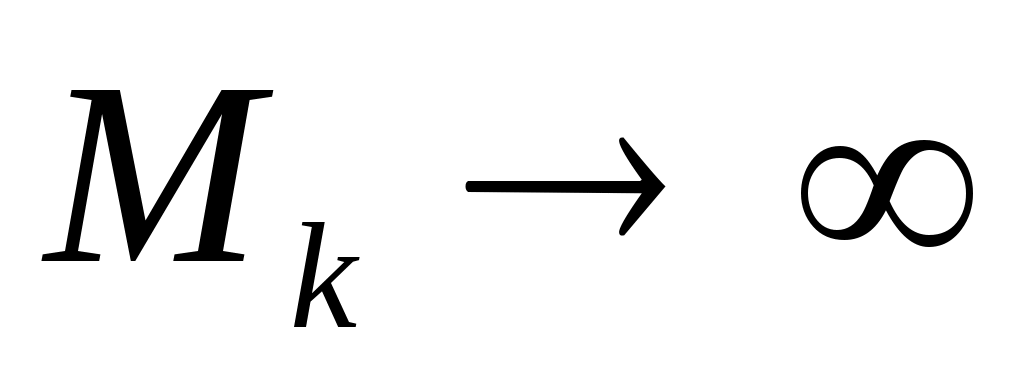 .
.
При каждом фиксированном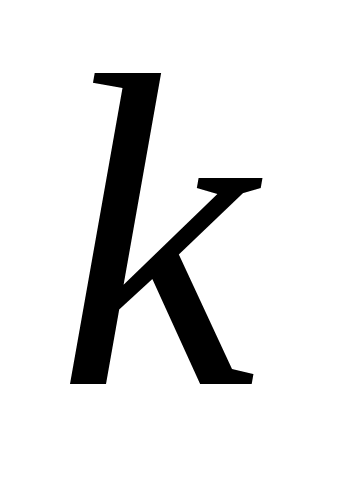 доказательство существования мы уже отметили, ибо
доказательство существования мы уже отметили, ибо  . Значит, мы имеем последовательность
. Значит, мы имеем последовательность 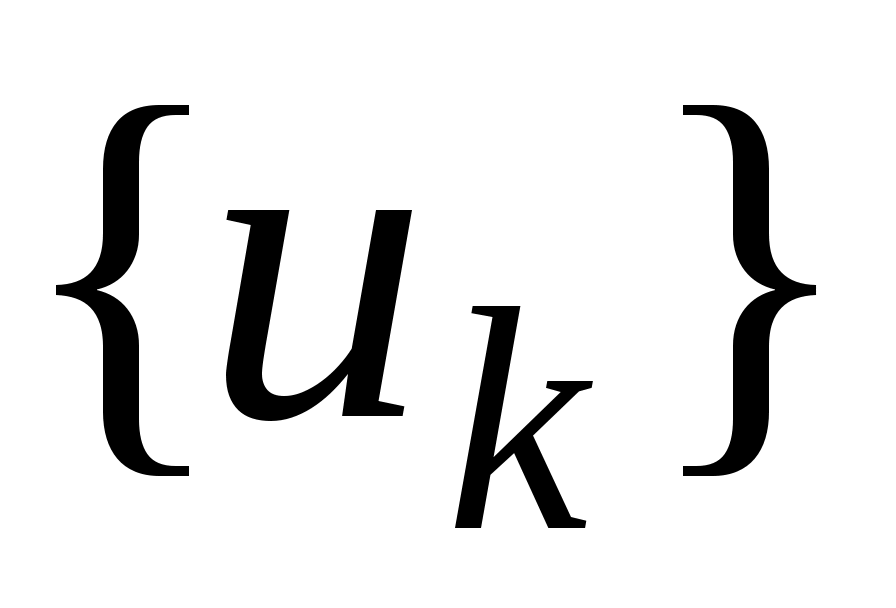 такую, что
такую, что
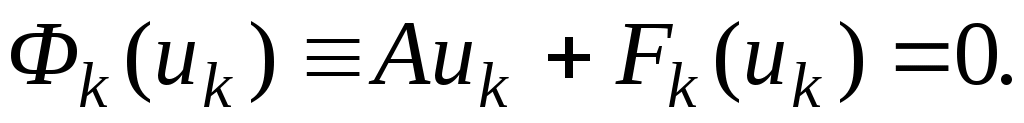
Из положительности и из (3) следует, что
и из (3) следует, что
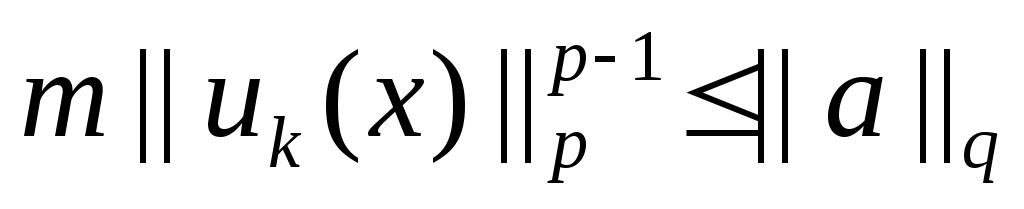
и что последовательность
На единичной окружности функцию из
Но если подставить
Значит
для любых
Этот пример говорит и о необходимости существенных дополнительных ограничений на операторы
Эти авторы так и поступили при доказательстве соответствующих утверждений в работах [3], [4].
Рассмотрим теперь уравнение (II).
Теорема 1.2. Пусть оператор
Тогда уравнение (II) имеет решение в
.
Если, кроме того, хотя бы один из операторов
Для доказательства строятся уравнения
Первое и третье слагаемые действуют из
Берем общий для
, имеющий такой смысл, что
Из коэрцитивности
Из тождества
Используя условия (1) и (2) получается
С учетом
,
Единственность решения доказывается как в предыдущей теореме.
Замечание 1.2. Если
Теорема 1.3. Пусть функция
Пусть далее
Доказательство. В случае
непрерывный, монотонный в
При
с сохранением монотонности
При каждом фиксированном
Из положительности
и что последовательность
