ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 106
Скачиваний: 0
СОДЕРЖАНИЕ
12Й вопрос. Закон всемирного тяготения. Гравитационное поле ,его напряженность.
13Й вопрос. Первая,вторая и третья космические скорости.
14Й вопрос. Неинерциальные системы отсчета. Силы инерции. Центробежная сила инерции .Сила Кориолиса.
16Й вопрос. Релятивистское выражение для импульса, полной и кинетической энергии.
19Й вопрос. Вязкость. Сила внутреннего трения. Ламинарное и турбулентное течения. Число Рейнольдса.
20Й вопрос. Взаимодействие двух точечных электрических зарядов.Закон Кулона.
26Й вопрос. Постоянный эл. Ток. Сила тока, плотность тока. Эдс, падение напряжения.
29Й вопрос. Разветвленные цепи.Правило Киргофа.
31ЙЗакон Био-Савара-Лапласа. Расчет поля бесконечного прямолинейного проводника с током.
33Й вопрос. Закон Ампера. Сила взаимодействия двух параллельных бесконечно длинных прямых токов.
40Й математический и физический маятники.Энергия гармонических колебаний.
52Й уравнение волны, волновая поверхность. Плоская и сферические волны, гармонические волны.
53Й энергия упругой волны. Плотность энергии, плотность потока энергии, интенсивность.
54Й эФфект доплера для звуковых волн.
55Й плоская электромагнитная волна,её свойства.
56Й энергия электромагнитных волн.Вектор пойнтинга.Интенсивность света.
1Й вопрос. Кинематика материальной точки: система координат, радиус-вектор, скорость, ускорение, траектория, перемещение , путь.
Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения, без выяснения причин, вызывающих это движение.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Положение точки характеризуется координатами x;y;z; и радиус вектором r
Радиус-вектор — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.).
Скорость - векторная величина, характеризующая быстроту изменения перемещения в пространстве.
Траектория – линия, описывающая точку в пространстве.
Перемещение – вектор, проведенный из начального положения движущейся точки в конечное её положение.
Путь - длина участка траектории пройденной телом.
Ускорение – ФВ ,характеризующая быстроту изменения скорости по модулю и направлению.
2Й вопрос. Кинематика материальной точки: тангенсальное, нормальное и полное ускорение, движение по окружности.
Тангенсальное
ускорение-первая
производная по времени от модуля
скорости, определяет быстроту изменения
скорости по модулю a=lim(![]() v/
v/![]() t)
(при
t)
(при
![]() v-->0
)
v-->0
)
Нормальное
ускорение
направленно по нормали к траектории, к
центру ее кривизны, определяет быстроту
изменения скорости по направлению
a=lim(![]() v/
v/![]() t)=v^2/r
(при
t)=v^2/r
(при
![]() t-->0)
t-->0)
Полное ускорение - геометрическая сумма тангенсального и нормального.
Движение по окружности S=Rф V=Rw; w=dф/dt(dt->0) a(tan)=(w^2)R;
В случае равнопеременного движения E=0 w=w0+Et ф=w0t+E(T^2)/2
3Й вопрос. Абсолютно твердое тело, Поступательное и вращательное движение. Кинематика вращательного движения: угловая скорость, угловое ускорение.
Абсолютно твердое тело – это тело, расстояние, между произвольными точками которого, остается постоянным
Поступательное движение - при котором любая прямая жестко связанная с движущимся телом параллельна первоначальному положению.
Вращательное движение - при котором все точки тела движутся по окружности, центры которых расположены на одной и той же прямой, называемой осью вращения.
Угловая
скорость
векторная величина, равная первой
производной угла поворота по времени.
w=lim(![]() ф/
ф/![]() t)=dФ/dt
(при дель t-->0)
t)=dФ/dt
(при дель t-->0)
(*Вектор w направлен вдоль оси вращения по правилу правого винта) .
Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени:
E=
(![]() w/
w/![]() t).
t).
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор E сонаправлен вектору w, при замедленном - противонаправлен ему.
4Й вопрос. Законы Ньютона. Инерциальная система отсчета. Закон сохранения импульса. Замкнутая система. Центр инерции системы частиц. Закон сохранения центра инерции.
Первый закон Ньютона: Всякая матер. точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения назыв. инертностью . Поэтому первый закон Ньютона назыв. также законом инерции.
Второй закон Ньютона(основной закон динамики поступательного движения)-отвечает на вопрос: как изменяется мех. движение матер. точки(тела) под действием приложенных к ней сил.
a~ F (m=const)
a~ 1/m (F=const)
a=kF/m.
Это соотношение выражает 2й закон Ньютона: ускорение, приобретаемое матер точкой (телом), совпадает по направлению с действующей на неё силой и равно отношению этой силы к массе материальной точки.
СИ коэф. пропорц. k=1.Тогда a=F/m или F=ma=m(dv/dt)
Третий закон Ньютона: Всякое действие матер точек (тел) друг на друга носит хар-ер взаимодействия; силы, с которыми действуют друг на друга матер. точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой соединяющих эти точки:
F1= -F2
Инерциальная система отсчета – это такая система, которая либо покоится, либо движется прямолинейно и равномерно.
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.
Центр инерции (центр масс) - воображаемая точка, положение которой характеризует распределение массы этой системы.
Центр масс движется равномерно или прямолинейно.
Центром масс (или центром инерции) системы материальных точек называется точка С, радиус-вектор которой равен:
(стр.18 самый низ)
где mi и ri – масса и радиус-вектор i-й материальной точки, а n- число материальных точек в системе
масса системы.
5Й вопрос. Движение тела с переменной массой. Реактивное движение. Уравнение Мищерского, Формула Циолковского.
Движение тела с переменной массой.
Если в момент времени t масса ракеты m, а ее скорость v,то по истечении времени dt ее масса уменьшится на dm и станет равной m-dm,а скорость станет равной v+dv.
Изменение импульса систем называется отрезок времени dt
dp=[(m-dm)(v+dv)+dm(v+u)]-mv, где u-скорость истечения газов относительно ракеты.Тогда
dp=mdv+udm
Если на систему действуют внешние силы, то dp=Fdt, поэтому
Fdt=mdv+udm, или m(dv/dt)=F-u(dm/dt)
Второе слагаемое в правой части этого ур-ия назыв. реактивной силой Fр. Если u противоположен v по направлению ,то ракета ускоряется а если совпадает с v, то тормозится .Таким образом, мы получили уравнение движения тела переменной массы
Реактивное движение- движение, возникающее при отделение от тела с некоторой скоростью его части .
ma=F+Fр (это ур-ие Мищерского)
![]()
где:
-
 —
масса материальной
точки переменной массы,
изменяющаяся за счет обмена частицами
с окружающей средой;
—
масса материальной
точки переменной массы,
изменяющаяся за счет обмена частицами
с окружающей средой; -
 —
скорость
движения материальной
точки переменной массы;
—
скорость
движения материальной
точки переменной массы; -
 —
внешние
силы, действующие на материальную
точку переменной массы со
стороны её внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.);
—
внешние
силы, действующие на материальную
точку переменной массы со
стороны её внешнего окружения (в том
числе, если такое имеет место, и со
стороны среды, с которой она обменивается
частицами, например электромагнитные
силы — в случае массообмена с
магнитной средой, сопротивление среды
движению и т. п.); -
 —
относительная
скорость присоединяющихся частиц;
—
относительная
скорость присоединяющихся частиц; -
 —
относительная
скорость отделяющихся частиц;
—
относительная
скорость отделяющихся частиц; -
 ,
, 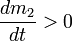 —
скорости массообмена присоединяющихся
и отделяющихся частиц;
—
скорости массообмена присоединяющихся
и отделяющихся частиц;
Полагая F=0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна(движется прямолинейно),получим
m(dv/dt)= -u(dm/dt),откуда
v= -u•(интег)dm/m= -u•lnm+C
Значение постоянной интегрирования С определим из нач. условии. Если в нач. момент времени скорость ракеты=0, а ее стартовая масса m0, то C=u•lnm0.Следовательно
v=u•ln(m0/m)
Это отношение назыв. формулой Циолковского.
6Й вопрос. Динамика вращения движения: момент силы ,момент импульса. Основной закон динамики вращ. Дв.
Момент силы F относительно неподвижной точки О назыв. физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы,на силу F.
М=[r•F], здесь М- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F.
Модуль момента силы
М=Frsina=Fl, где а-угол м-ду r и F; rsina=l - кратчайшее растояние м-ду линией действия силы и точкой О-плечо силы.
Mz=Jz(dw/dt)=JzE, где Е-ускорение вр. движ.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Основной закон динамики вращательного движения твердого тела формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.
Это ур-ие представляет собой ур-ие динамики вращ. движения твердого тела относительно неподвижной оси.
Производная момента импульса по времени, относительно полюса О равна моменту внешних сил относительно полюса.
dL/dt=M
(ситема из 3х ур-ий):
dLx/dt=Mx
dLy/dt=My
dLz/dt=Mz
