Файл: физика ответы на экзамен 2 сесестр.doc

Длина тел:

Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных СО. Таким образом, линейные размеры тела наибольшие в той инерциальной СО относительно которой тело покоится.

l=l' • sqrt1-b^2

b=V/c

16Й вопрос. Релятивистское выражение для импульса, полной и кинетической энергии.

Масса движушихся релятивистских частиц зависит от их скорости:

m=m0/sqrt 1-b^2 , где m0 - масса покоя частицы, т.е. масса, измеренная в той инерциальной СО, относительно которой она находится в покое, m - масса частицы в сист. отсчета, относительно которой она движется со скоростью V.

F=dp/dt=d(mV)/dt

Основной закон релятивистской динамики материальной точки имеет вид F=d(m0V/sqrt(1-b^2))/dt или F=dp/dt' , где p=mV=m0V/sqrt(1-b^2) - релятивистский импульс материальной точки.

Полная энергия частицы:

(дельта E)=c^2 • (дельта m) , откуда

E=mc^2=m0c^2/sqrt 1-b^2

Кинетическая енергия имеет вид:

dT=dA или dT=Авк

Учтем, что dr=Vdt

dT=(d(m0V/sqrt(1-b^2))/dt)•Vdt=Vd(m0V/sqrt(1-b^2))

Учтем, что VdV=vdv

dT=d(m0•c^2)/sqrt(1-b^2)=c^2•dm проинтегрировав, получим T=(m-m0)c^2 или

T=m0c^2((1/sqrt1-b^2) – 1)

Релятивистский импульс

Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ.

Тогда .

 Релятивистское выражение для энергии

В релятивистской механике справедливым остается выражение

.                                                                                 

Это означает, что 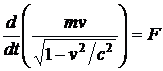. Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.

Легко получить выражение для кинетической энергии. Поскольку

dE_k = dA  и dE_k = v·p·dt, dA = F·ds

.                                                               

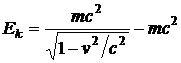 Отсюда следует, что E₀ = mc² является энергией покоя. Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:

Взаимосвязь массы и энергии. Границы применимости механики Ньютона.

17Й вопрос. Гидродинамика. Линии тока и трубки тока. Теорема о неразрывности струи. Течение идеальной жидкости. Уравнение Бернулли, Формула Торричелли.

Гидродина́мика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

В жидкости или газе мысленно проводятся линии так, что скорость частиц в каждой точке направлена по касательной к линии, т.е. линия является траекторией. Такие линии называются линиями тока.

Объем, ограниченный линиями тока, называется трубка тока. В силу построения частицы не пересекают стены трубки.

Теорема о неразрывности струи - произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока SV = const; S1V1=S2V2

Течение идеальной жидкости: плотность=const, энгэ(вязкость)=0; где отсутствует внутреннее трение.

рV^2/2 + рgh + Po=const - ур-ние Бернули, где p - плотность, а Po - давление.

Ф-ла Торричелли v2=sqrt(2g(h1-h2))=sqrt(2gh); когда v2<<v1.

18Й вопрос. Гидродинамика. Полное, динамическое и статическое давление. Трубка Пито, зонд, трубка Пито-Прандтля.

Гидродина́мика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа. Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Для горизонтальной трубки тока выражение P+p(v^2)/2-полное давление Из уравнения Бернулли pV^2/2+pgh+P P-статическое давление, жидкости на поверхности обтекаемого ею тела.

pv^2/2- динамическое давление (кинетическая энергия)

Трубка Пито - представляет собой трубку с отверстием на конце, подсоединенную к монометру. (см. рис. 5.)

В точке 1 параметры невозмущенного тока. p1+(mV1^2)/2=p2

p1 - давление в невозмущенном потоке (статическое давление)

(mV1^2)/2 - динамическое давление

p2 - полное давление.

Зонд - изогнутая трубка с боковыми отверстиями. (см. рис. 6.)

В силу обтекаемости в трубке в точке 1 такие же параметры, как в точке 2, значит зонд измеряет статическое давление.

Если зонд и трубку Пито подсоединить к дифференциальному монометру (измеряющему разность давления), то монометр покажет динамическог давление (трубка Пито - Прандтля).

(остальное написано Боряном)

Так как динамическое давления связанно со скоростью движения жидкости, то уравнение Бернулли позволяет измерять скорость потока жидкости. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоедены к манометру с помощью одной из трубок измеряют полное давление P0, а с помощью другой статическое, манометром измеряют разность давления.

Разность полного и статического давления - равна динамическому давлению. P0-P=pv^2/2 из этого скорость равна v=sqrt(2p0gh/p)

19Й вопрос. Вязкость. Сила внутреннего трения. Ламинарное и турбулентное течения. Число Рейнольдса.

Вязкость-свойство реальных жидкостей оказывть сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила. Величина (дельта V)/(дельта x) показывает, как быстро меняется скорость при переходе от слоя к слою в направлении x, перпендикулярном направлению движения слоев и называется градиентом скорости. Таким образом, модуль силы внутреннего трения

F=энгэ(вязкость)•S•|(дельта V)/(дельта x)| , где энгэ - динамическая вязкость (Па•с)

Ламинарное (слоистое) течение-если вдоль потока каждый выделеный тонкий слой скользит относительно соседних не перемешиваясь с ними.

Турбулентное (вихревое) течение - если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Характер течения зависит от безразмерной величины чила Рейнольдса Re=плотность ( т.е. ро) • <V>d/энгэ(вязкость)=<V>•d/ню, где ню=энгэ/ро - кинематическая вязкость; ро - плотность жидкости, <V> - средняя по сечению трубы скорость жидкости; d - характерный линейный размер (диаметр трубы).

при Re<1000 - наблюдается ламинарное

при 1000 <= Re <= 2000 - область перехода от ламинарного течения к турбулентному

при Re>2000 - наблюдается турбулетное

20Й вопрос. Взаимодействие двух точечных электрических зарядов.Закон Кулона.

F=kq1q2/r^2 Точечным называестя заряд сосредоточенный на теле, линейные размеры которого пренебрежительно малы по сравнению с расстоянием до других тел с которыми он взаимодействует. k=1/4ПиE0, E0 = 8,85•10^(-12) Ф/м - электрическая постоянная.

21Й вопрос. Потенциальная энергия взаимодействия двух точечных эл. Зарядов. Потенциал поля точечного заряда. Эквипотннциальные поверхности. Система эл. Зарядов. Потенциал поля,энергия взаимодействия.

Потенциальная энергия еденичного заряда определяемая потенциалом.

U=k•q1q2/r

Потенциал - работа по перемещению еденичного положительного заряда при удалении его из данной точки поля в бесконечность - энергетическая характеристика поля.

фи=kq/r , Кл/м

фи=A (бесконечная)/q0

Эквипотенциальная поверхность - поверхность, во всех точках которой потенциал имеет одно и то же значение.

Система эл. зарядов. Потенциал системы зарядов = алгебраической сумме потенциалов отдельных зарядов.

Потенциал системы - алгебраическая сумма всех потенциалов поля.

фи(i)=k•(знак суммы; n, i=1)Q(i)/R(i)

22Й вопрос. Напряженность эл. Поля точечного заряда и системы зарядов.Принцип суперпозиции.Линии напряженности.Связь м-ду напряженностью эл. Поля и потенциалом.Эквипотенциальные поверхности.

Напряженность - сила, действующая на пробный единичный положительный заряд. E=F/q0 или k•q/r^2 - силовая характеристика поля. Направление вектора E совпадает с вектором силы, действующей на положительный заряд.

Принцип суперпозиции - напряженность результирующего поля - геометрическая сумма напряженности полей, создаваемых в точке зарядами по отдельности. E=(знак суммы, n, i=1)E(i).

Линии напряженности - линии, касательные к которым в каждой точке совпадают с направлением вектора Е.

Эквипотенциальх поверхностей вокруг заряда можно провести бесконечное множество. Однако их обычно проводят так, чтобы разность потенциалов была одинакова, зная расположение линий напряженности электростатического поля можно построить эквипотенциальные поверхности.