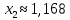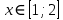ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
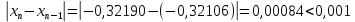, поэтому останавливаем вычисления. Округлим значение до тысячных и получим: 
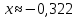
Ответ:
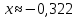.ЗАДАНИЕ 3
-
Отделить корни графически и уточнить один из них методом хорд с точностью до 0,001
Корень находится в промежутке [0,5; 1] (установлено в задании 2).
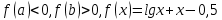
Поэтому касательную будем проводить через точку a = 0,5.
Начальное приближение
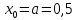.Вычисления проводим по формуле:
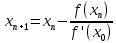
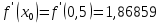
Представим вычисления в виде таблицы:
| n |  |  |  |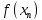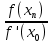
| 0 | 0,5 | 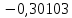 | -0,16110 |
| 1 | 0,66110 | -0,01863 | -0,00997 |
| 2 | 0,67107 | -0,00216 | -0,00116 |
| 3 | 0,67223 | -0,00025 | -0,00013 |
| 4 | 0,67236 | | |
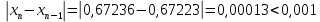, поэтому останавливаем вычисления. Округлим значение до тысячных и получим: 
Ответ:
.-
Отделить корни аналитически и уточнить один из них методом касательных с точностью до 0,001
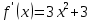
Корень находится в промежутке [-1; 0].
Выясним знак второй производной:
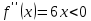на промежутке [-1; 0].
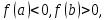начальное приближение 
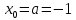.Вычисления проводим по формуле:
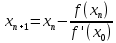
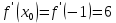
Представим вычисления в виде таблицы:
| n | |  |  |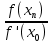
| 0 | -1 | -3 | -0,5 |
| 1 | -0,5 | -0,625 | -0,10417 |
| 2 | -0,39583 | -0,24951 | -0,04159 |
| 3 | -0,35421 | -0,10719 | -0,01787 |
| 4 | -0,33635 | -0,04709 | -0,00785 |
| 5 | -0,32850 | -0,02095 | -0,00349 |
| 6 | -0,32501 | -0,00936 | -0,00156 |
| 7 | -0,32345 | -0,00419 | -0,00070 |
| 8 | -0,32275 | | |
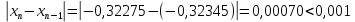, поэтому останавливаем вычисления. Округлим значение до тысячных и получим: 
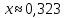
Ответ:
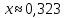.ЗАДАНИЕ 4
Комбинированным методом хорд и касательных решить уравнение, вычислив корни с точностью до 0,001.
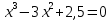
Отделим корни аналитически.
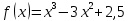
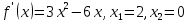
Таблица знаков функции:
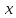 | -∞ | 0 | 2 | +∞ |
 | - | + | - | + |
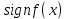Уравнение имеет три действительных корня. Уменьшим промежутки:
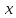| | -1 | 0 | 1 | 2 | 3 |
| | - | + | + | - | + |
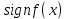Корни находятся в промежутках:
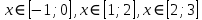
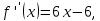
Уточним корни.
-
.
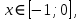
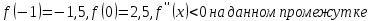Знак функции совпал со знаком второй производной на левом конце, следовательно, касательные начнем строить, начиная с левого конца, а хорды проводить с подвижным правым. Используем формулы:
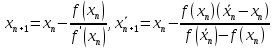
– точки пересечения касательной и хорд, значения корня по недостатку и по избытку соответственно.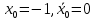
Обозначим:
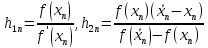
Вычисления в таблице:
 | |  | |  |  |  |
 |  |  | ||||
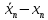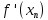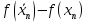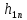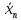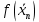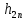| 0 | -1 | 1 | -1,5 | 9 | 3,5 | -0,16667 |
| 0 | 2,5 | -0,42857 | ||||
| 1 | -0,83333 | 0,2619 | -0,16201 | 7,08330 | 1,49582 | -0,02287 |
| -0,57143 | 1,33381 | -0,02837 | ||||
| 2 | -0,81046 | 0,0055 | -0,00288 | 6,83330 | 0,03742 | -0,00042 |
| -0,80496 | 0,03454 | -0,00042 | ||||
| 3 | -0,81004 | 0 | | | | |
| -0,81004 |
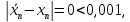останавливаем вычисления. Округлим до тысячных и получим: 
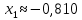
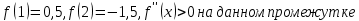.Знак функции совпал со знаком второй производной на левом конце, следовательно, касательные начнем строить, начиная с левого конца, а хорды проводить с подвижным правым. Используем формулы:
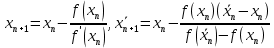
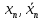– точки пересечения касательной и хорд, значения корня по недостатку и по избытку соответственно.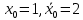
Обозначим:
Вычисления в таблице:
| | |  | |  |  |  |
 |  |  | ||||
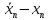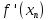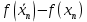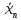| 0 | 1 | 1 | 0,5 | -3 | -2 | -0,16667 |
| 2 | -1,5 | -0,25 | ||||
| 1 | 1,16667 | 0,08333 | 0,00462 | -2,91666 | -0,239 | -0,00158 |
| 1,25 | -0,23438 | -0,00161 | ||||
| 2 | 1,16825 | 0,00003 | | | | |
| 1,16828 | | |
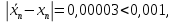останавливаем вычисления. Округлим до тысячных и получим: 