Файл: Дифференциальное и интегральное исчисления функции одной переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение
высшего образования
«Северный (Арктический) федеральный университет имени М.В. Ломоносова»
Высшая школа энергетики нефти и газа
_____________________________________________________
(наименование высшей школы / филиала / института / колледжа)
КОНТРОЛЬНАЯ РАБОТА
| По дисциплине/междисциплинарному курсу/модулю | Высшая математика | |
| | ||
| | ||
| На тему | Дифференциальное и интегральное исчисления функции одной переменной. Дифференциальные уравнения. Вариант 8 | |
| | ||
| | Выполнил (-а) обучающийся (-аяся): Заболотский Юрий Иванович |
| | (Ф.И.О.) |
| | Направление подготовки / специальность: 13.03.01 Теплоэнергетика теплотехника |
| | (код и наименование) |
| | Курс: 1 |
| | Группа:113205 |
| | Руководитель: Попов Василий Николаевич, профессор |
| | (Ф.И.О. руководителя, должность / уч. степень / звание) |
| Отметка о зачете | | | | |
| | | (отметка прописью) | | (дата) |
| Руководитель | | | | |
| | | (подпись руководителя) | | (инициалы, фамилия) |
Архангельск 2022
Задание 1
8. а)
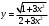 , б)
, б) 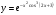 , в)
, в) 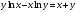 .
.Решение
а)
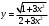 .
.Используя правило дифференцирования частного, правило дифференцирования сложной функции и табличные формулы, получим:
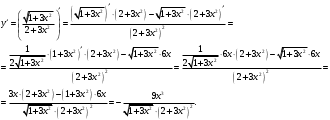
б)
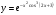 .
.Используя правило дифференцирования произведения, правило дифференцирования сложной функции и табличные формулы, получим:
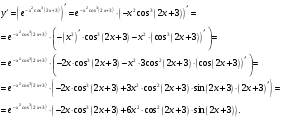
в)
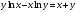 .
.Функция задана неявно в виде
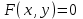 .
.Дифференцируем обе части данного уравнения, считая
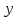 функцией от
функцией от  :
:
Выразим из уравнения
 :
: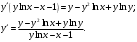
Задание 2
Исследовать методами дифференциального исчисления функцию и построить ее график, используя результаты исследования.
8.
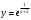
Решение
Для полного исследования функции и построения ее графика применяется следующая примерная схема:
-
найти область определения функции; -
исследовать функцию на непрерывность и определить характер точек разрыва; -
исследовать функцию на четность и нечетность, периодичность; -
найти точки пересечения графика функции с осями координат; -
исследовать функцию на монотонность и экстремум; -
найти интервалы выпуклости и вогнутости, точки перегиба; -
найти асимптоты графика функции; -
по полученным данным построить график функции.
Применим вышеуказанную схему для исследования данной функции.
-
 .
. -
Функция не определена в точке . Следовательно,
. Следовательно,  есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:
есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:
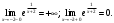
Следовательно,
 – точка разрыва второго рода;
– точка разрыва второго рода;-
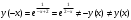 .Функция не является ни четной, ни нечетной. Функция не периодическая.
.Функция не является ни четной, ни нечетной. Функция не периодическая. -
С осью Ох точек пересечения нет.
С осью Оу:
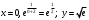 .
.Точка
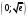 – точка пересечения с осью Оy.
– точка пересечения с осью Оy.-
Находим производную.
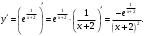
 при
при 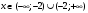 и не существует при
и не существует при 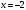 .
.Критических точек нет.

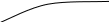

 – –
– – 
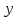 –2
–2 Функция убывает на всех
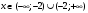 .
.-
Находим вторую производную.

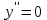 при
при 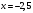 и не существует при
и не существует при 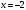 .
.Критическая точка второго рода:
 .
.
 - + +
- + + 
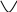
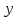 -2,5 -2
-2,5 -2 Функция вогнута на интервалах
 , функция выпукла на интервале
, функция выпукла на интервале 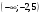 .
.Точка перегиба
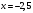 ,
, 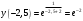 .
.-
Так как точка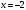 - точка разрыва второго рода, то прямая
- точка разрыва второго рода, то прямая 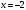 - вертикальная асимптота.
- вертикальная асимптота.
Найдем наклонные асимптоты

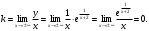

Тогда
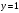 - горизонтальная асимптота
- горизонтальная асимптота-
По полученным данным строим график функции.
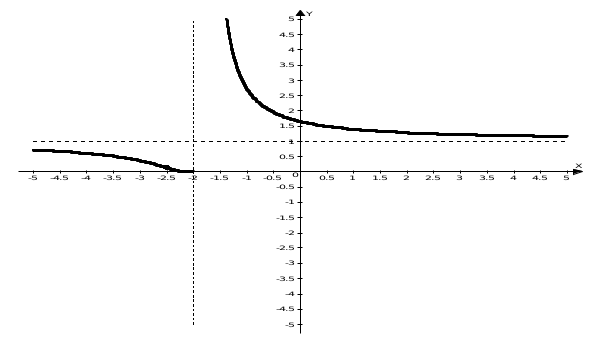
Задание 3
Найдите неопределенные интегралы. В п. а) и б) результаты проверить дифференцированием.
8. а)
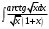 ; б)
; б)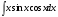 ;
;в)
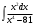 ; г)
; г) 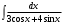 .
.Решение
а)
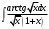 .
.Применим подстановку
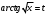 :
:
Проверка:
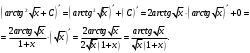
б)
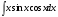 ;
;Применим формулу интегрирования по частям
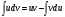 .
. 
Проверка:
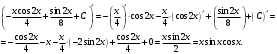
в)
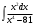 .
.Разложим подынтегральную дробь на сумму простейших дробей:

Коэффициенты
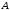 ,
,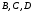 найдем из условия:
найдем из условия: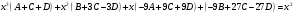 .
. Приравняем коэффициенты с одинаковыми степенями при x:
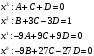 откуда
откуда 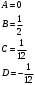
Таким образом,
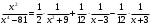 .
.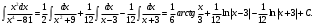
г)
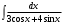 ;
;Для преобразования подынтегральной функции применим формулы универсальной тригонометической подстановки
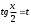 .
. 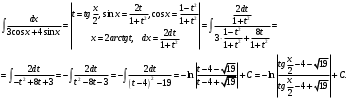
Задание 4
Вычислите определенные интегралы.
8.
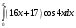 .
.Решение
Находим интеграл с помощью формулы интегрирования по частям
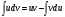 и применим формулу Ньютона-Лейбница:
и применим формулу Ньютона-Лейбница: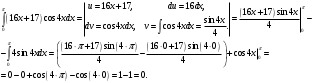
Ответ: 0.
Задание 5
Найдите общее решение дифференциального уравнения.
8. а)
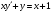 ; б)
; б)  .
.Решение
а)
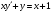 .
.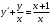
Это линейное дифференциальное уравнение первого порядка. Будем искать решение в виде
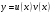 , тогда
, тогда 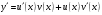 . После подстановки
. После подстановки 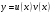 и выражения для производной в уравнение получим
и выражения для производной в уравнение получим


