Файл: Дифференциальное и интегральное исчисления функции одной переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
.
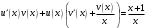Потребуем:
.
Получаем систему:
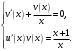
Решим уравнение .
Получаем:
.
.
.
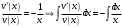откуда при C =0:
и искомая функция будет иметь вид:
.
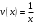После подстановки функции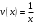 во второе уравнение, получим
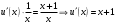. Решим последнее уравнение:
,
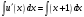Тогда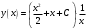
– общее решение исходного уравнения.
б)
.
.
Имеем дифференциальное уравнение второго порядка, допускающее понижение порядка, так как не содержит
Введем подстановку: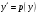
, 
.
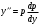Получаем:
.
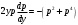Получаем:
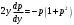
Разделяя переменные, последовательно находим:
;
;
;
;
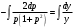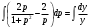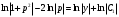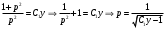
С учетом подстановки:
.
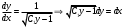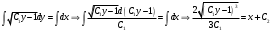– общий интеграл.
При решении было упущено решение: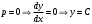
.
Задание 6
Решите задачу Коши
8.
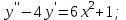
Решение.
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:
,
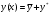где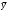
– общее решение соответствующего однородного уравнения,
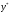– частное решение исходного неоднородного уравнения.
1) Найдем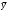 – общее решение соответствующего однородного уравнения, т.е. уравнения:
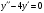
Для этого составляем характеристическое уравнение:
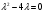
Получаем: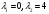
.
Эти корни являются действительными разными, поэтому система решений, соответствующая этим корням, будет иметь вид:
.
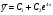2) Найдем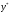 – частное решение исходного неоднородного уравнения.
Частное решение неоднородного уравнения будем искать в виде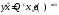
.
В нашем случае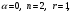
так как 
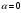один раз встречается среди корней характеристического уравнения.
Итак,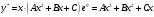
, где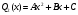 
это многочлен второй степени.
Находим: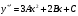
.
.
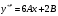Подставляем в исходное уравнение:
.
.
.
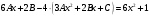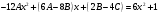
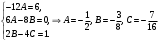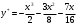Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:
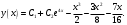
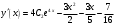
Воспользуемся начальными условиями:
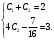
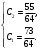
Тогда искомое частное решение:
.
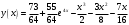Ответ: .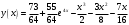
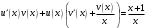.Потребуем:
.Получаем систему:
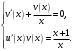
Решим уравнение
.Получаем:
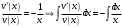. . .откуда при C =0:
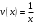и искомая функция будет иметь вид: .После подстановки функции
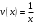во второе уравнение, получим 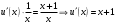. Решим последнее уравнение: 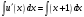, Тогда
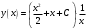– общее решение исходного уравнения.б)
. .Имеем дифференциальное уравнение второго порядка, допускающее понижение порядка, так как не содержит
Введем подстановку:
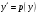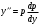, .Получаем:
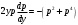.Получаем:
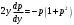
Разделяя переменные, последовательно находим:
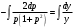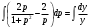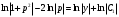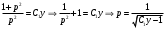
; ; ; ; С учетом подстановки:
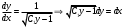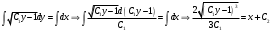. – общий интеграл.При решении было упущено решение:
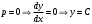.Задание 6
Решите задачу Коши
8.
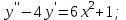
Решение.
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:
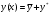, где
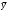– общее решение соответствующего однородного уравнения, 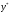– частное решение исходного неоднородного уравнения.1) Найдем
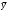– общее решение соответствующего однородного уравнения, т.е. уравнения: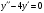 Для этого составляем характеристическое уравнение:
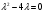
Получаем:
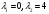. Эти корни являются действительными разными, поэтому система решений, соответствующая этим корням, будет иметь вид:
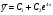.2) Найдем
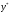– частное решение исходного неоднородного уравнения.Частное решение неоднородного уравнения будем искать в виде
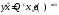.В нашем случае
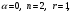так как 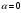один раз встречается среди корней характеристического уравнения.Итак,
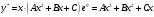, где 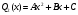это многочлен второй степени. Находим:
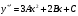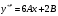. .Подставляем в исходное уравнение:
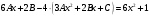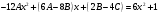
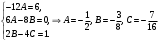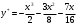. . .Общее решение y(x) исходного линейного неоднородного дифференциального уравнения имеет вид:
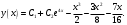
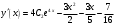
Воспользуемся начальными условиями:
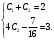
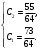
Тогда искомое частное решение:
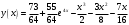.Ответ:
.
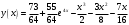