Разработка учебных заданий для формирования предметных, метапредметных и личностных результатов освоения образовательной программы по математике 5 кл.

Базовые исследовательские действия:

• 
  использовать вопросы как исследовательский инструмент познания; формулировать вопросы, фиксирующие противоречие, проблему, самостоятельно устанавливать искомое и данное, формировать гипотезу, аргументировать свою позицию, мнение;
  
• 
  проводить по самостоятельно составленному плану несложный эксперимент, небольшое исследование по установлению особенностей математического объекта, зависимостей объектов между собой;
  
• 
  самостоятельно формулировать обобщения и выводы по результатам проведённого наблюдения, исследования, оценивать достоверность полученных результатов, выводов и обобщений;
  
• 
  прогнозировать возможное развитие процесса, а также двигать предположения о его развитии в новых условиях.
  

1. 
   На развертке прямоугольного параллелепипеда буквами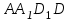 обозначена одна его грань. Соотнеси изображение прямоугольного параллелепипеда с его разверткой и назови грани прямоугольного параллелепипеда, на которых расположены точки , , .
   

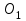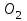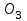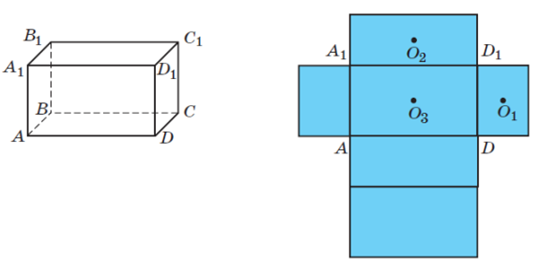
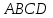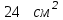Какими могут быть длина, ширина и высота этого параллелепипеда, если площадь грани – , а площадь грани 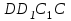– 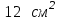? Начерти такую же таблицу и запиши все возможные варианты измерений данного параллелепипеда.

---

Длина (см)	2	4
Ширина (см)
Высота (см)

2. 
   В 5 «Е» классе 30 учеников. Их приглашают в медицинский кабинет одинаковыми группами по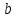 человек. Сколько ребят может быть в одной группе, если ?
   

3. 
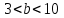   Может ли сумма двух чисел делиться на натуральное число, если каждое слагаемое не делится на это число? Если «да», то приведи примеры.
   

4. 
   Пользуясь схемой, запиши, чему равен отрезок ?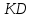
   

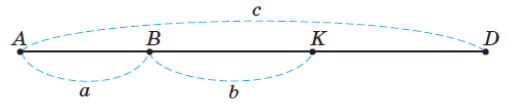
Один ученик ответил так: .

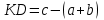Другой ученик ответил так: .

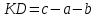Третий ученик ответил так:

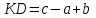
Объясни, как рассуждали эти ученики, кто из них прав, и сформулируй правило, как вычесть сумму из числа.
Базовые логические действия:

• 
  выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;
  
• 
  воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие; условные;
  
• 
  выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях; предлагать критерии для выявления закономерностей и противоречий;
  
• 
  делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии;
  
• 
  разбирать доказательства математических утверждений (прямые и от противного), проводить самостоятельно несложные доказательства математических фактов, выстраивать аргументацию, приводить примеры и контрпримеры; обосновывать собственные рассуждения;
  
• 
  выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).
  

---

5. 
   Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9», Роман заверил, что «это простое число», Катя утверждает, что «это число чётное», а Наташа думает, что «это число 15». Какое число в ответе задачи, если известно, что одна девочка и один мальчик ошиблись?
   

Кто мог ошибиться? Рассмотри все предположения и приведи рассуждения, заполнив таблицу.

Предположения Выска- зывания	Предположим, что ошиблись
	Коля и Катя
Коля: 9	-
Роман: простое	Простое
Катя: четное	-
Наташа: 15	15
Вывод	Предположение ложное, так как число 15 не простое

Работа с информацией:

• 
  выявлять недостаточность и избыточность информации, данных, необходимых для решения задачи;
  
• 
  выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;
  
• 
  выбирать форму представления информации и иллюстрировать решаемые задачи схемами, диаграммами, иной графикой и их комбинациями;
  
• 
  оценивать надёжность информации по критериям, предложенным учителем или сформулированным самостоятельно.
  

6. 
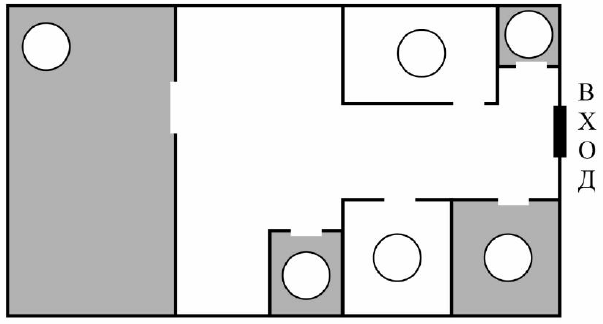
   Таня написала сочинение о торговом центре около её дома и нарисовала план торгового центра.
   

Недалеко от нашего дома находится небольшой торговый центр. Если войти в него с улицы, то сразу справа расположен киоск «Печать». Дедушка каждое утро покупает в нём газеты. Он говорит, что новости лучше всего знавать из газет, а не из телевизора или интернета. Рядом с киоском «Печать» находится зоомагазин. Раньше здесь была только еда и игрушки для животных. Но недавно появились живые рыбки, хомячки и попугаи. Теперь, когда я иду в книжный магазин, я обязательно заглядываю в зоотовары посмотреть на зверушек. Книжный магазин, про который я говорю, расположен сразу слева от входа, напротив киоска с газетами.

---

Рядом с книжным, напротив зоомагазина, аптека. Когда я прошлой зимой заболела ангиной, папа поздно вечером ходил в эту аптеку за лекарствами. Самое большое помещение в торговом центре занимает супермаркет. В нём можно купить продукты, зубную пасту, стиральный порошок и даже лампочки.

Да, чуть не забыла ещё про один магазин. Это магазин «Цветы». Он примыкает к аптеке, но не с той стороны, где книжный, а с другой.

Рассмотри план торгового центра. Пользуясь описанием, которое дала Таня, отметь на плане цифрами шесть объектов.

1. Киоск «Печать».

2. Супермаркет.

3. Зоомагазин.

4. Магазин «Цветы».

5. Аптека.

6. Книжный магазин.

7. 
   Каждый пятиклассник посещает одно из четырех занятий внеурочной деятельности. Информация представлена на круговых диаграммах.
   

Пользуясь диаграммами, заполни в тетради таблицу.

Класс	Всего уч-ся	Школьные кружки
		Юный исследователь		Наглядная геометрия		Учимся решать логические задачи		Учимся решать комбинаторные задачи
		Уч.	%	Уч.	%	Уч.	%	Уч.	%
5А
5Б
5В
Всего

---

Универсальные коммуникативные действия:

Сотрудничество:

• 
  понимать и использовать преимущества командной и индивидуальной работы при решении учебных математических задач; принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы; обобщать мнения нескольких людей;
  
• 
  участвовать в групповых формах работы (обсуждения, обмен мнениями, мозговые штурмы и др.); выполнять свою часть работы и координировать свои действия с другими членами команды; оценивать качество своего вклада в общий продукт по критериям, сформулированным участниками взаимодействия.
  

8. 
   Используя запись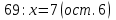 , составь уравнение и реши его.
   

Сравни свой ответ с двумя ниже приведенными решениями одноклассников.



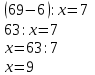
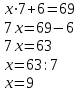
Как рассуждали твои одноклассники? Чьё решение тебе показалось более понятным? Чьё решение является более рациональным?

9. 
   Два пятиклассника умножали дробь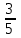 на натуральное число 4. Один из них сделал это так: 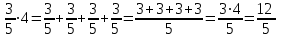, а другой предложил иное решение: 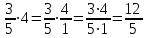. Какими приемами они пользовались, выполняя вычисления? Какой из способов тебе понравился больше? Какой из способов ты считаешь более рациональным? Попытайся сформулировать правило умножения дроби на натуральное число.
   

Универсальные регулятивные действия

Самоорганизация:

• 
  самостоятельно составлять план, алгоритм решения задачи (или его часть), выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации.
  

Самоконтроль:

• 
  владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;
  
• 
  предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, найденных ошибок, выявленных трудностей;
  
• 
  оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту.
  

---

Смотрите также файлы

• 1. Основные черты средневековой христианской философии. Схоластика. Учение Фомы Аквинского.pdf

• Календарнотематический план по предмету Русский язык и литература в 5м классе (c нерусским языком обучения) разработан на основании.docx

• 2. 2 Взаимодействие дошкольной образовательной организации с семьями воспитанников. Преемственность ооп дошкольного и начального образования.docx

• Доклад Выполнен ученицей 8 класса В ноу Гимназия 1 г. Новороссийска.doc

• Программа учителя иностранного языка Араповой Анжелики Андреевны для проведения дополнительных занятий.odt