Файл: Контрольная работа по дисциплине Теоретическая механика Вариант 38 Выполнил ст гр. Гд(ГО)з20 (группа).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 38
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное учреждение
высшего образования
«Забайкальский государственный университет»
(ФГБОУ ВО «ЗабГУ»)
Факультет Горный
Кафедра Открытые горные работы
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Теоретическая механика»
Вариант № 38
Выполнил ст. гр. ГД(ГО)з-20
(группа)
. Филинов А.С. .
(фамилия, инициалы)
Проверил к.п.н. доцент
Мурашко С.В.
(должность, ученая степень, звание, фамилия, инициалы)
Чита
2023
Контрольная работа
Вариант 38 (схема 3, вариант данных 8)
Задания С1, К2, Д1, Д4
Задание С1
Определение реакций опор твёрдого тела
На жёсткую ломаную раму (см. рис.1.4) действуют пара сил с моментом
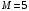 кН·м, распределённая нагрузка q и сила Р. Размеры элементов конструкции, величина, направление и точка приложения силы Р, а также закономерность распределенной нагрузки, её максимальные значения и участок действия принять согласно табл.1.1. Определить реакции в опорах, если
кН·м, распределённая нагрузка q и сила Р. Размеры элементов конструкции, величина, направление и точка приложения силы Р, а также закономерность распределенной нагрузки, её максимальные значения и участок действия принять согласно табл.1.1. Определить реакции в опорах, если 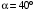 ,
, 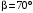 .
.Исходные данные:
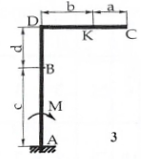
Рис.1.4
| Вариант | Схема распределения интенсивности | Участок | Расположение силы P | Точка приложения силы | 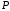 , кН , кН |  , м , м | 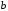 , м , м |  , м , м | 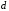 , м , м | Значение q или qmax, кН/м |
| 7 | 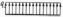 | KD | 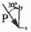 | С | 8 | 4 | 3 | 3 | 4 | 5 |
Решение
1. Рассмотрим равновесие рамы. Проведем координатные оси
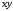 и изобразим действующие на раму силы (рис.1): заданные силу
и изобразим действующие на раму силы (рис.1): заданные силу 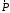 , пару сил с моментом
, пару сил с моментом 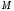 . Равномерно распределенную нагрузку
. Равномерно распределенную нагрузку 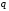 заменяем равнодействующей сосредоточенной силой
заменяем равнодействующей сосредоточенной силой 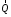 , точка приложения которой расположена на расстоянии, равном
, точка приложения которой расположена на расстоянии, равном 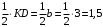 м (от точки D).
м (от точки D). При этом численно
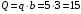 кН.
кН.Изображаем реакции связей
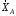 ,
, 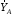 ,
, 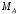 (реакцию жесткой заделки А изображаем двумя составляющими вдоль осей координат и реактивным моментом).
(реакцию жесткой заделки А изображаем двумя составляющими вдоль осей координат и реактивным моментом).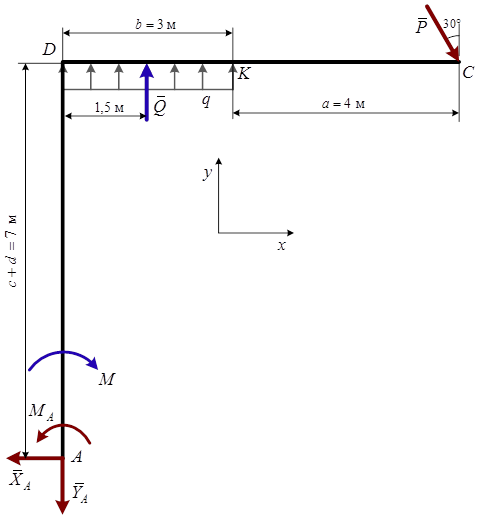
Рис.1. Расчетная схема конструкции
Для полученной плоской системы сил составляем три уравнения равновесия. При вычислении момента силы
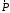 относительно точки А воспользуемся теоремой Вариньона, то есть мысленно разложим силу
относительно точки А воспользуемся теоремой Вариньона, то есть мысленно разложим силу 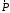 на составляющие
на составляющие 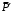 ,
, 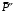 (
(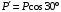 ,
, 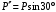 ) и учтем, что
) и учтем, что 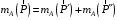 . В результате будем иметь:
. В результате будем иметь: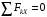 ,
, 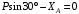 ; (1)
; (1)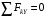 ,
, 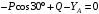 ; (2)
; (2)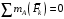 ,
, 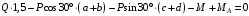 . (3)
. (3)Решаем систему уравнений (1)–(3) и находим реакции.
Из уравнения (1) находим
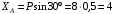
кН.
Из уравнения (2) получаем
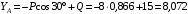 кН.
кН.Из уравнения (3) будем иметь
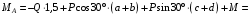
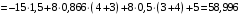 кН·м.
кН·м.Для проверки правильности полученных результатов составим и решим проверочное уравнение равновесия в форме моментов всех сил относительно точки K.
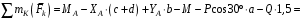
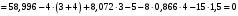 .
.Следовательно, реакции определены правильно.
Ответ:
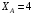 кН;
кН; 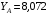 кН;
кН; 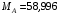 кН·м.
кН·м.Задание К2
Кинематический анализ плоского механизма
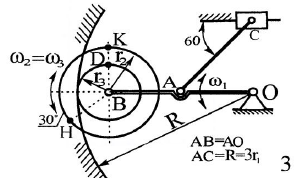
Механическая система в момент времени t занимает положение согласно рис.2.9. Определить кинематические параметры согласно табл. 2.2 и показать их направление на чертеже, если в момент t угловая скорость одного из элементов представлена как
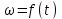 . При выборе исходных данных из табл.2.2 ω1, ω2, ω3 при их положительном значении считать вращение по часовой стрелке, при отрицательном значении – против часовой стрелки, значение ω1 принимать
. При выборе исходных данных из табл.2.2 ω1, ω2, ω3 при их положительном значении считать вращение по часовой стрелке, при отрицательном значении – против часовой стрелки, значение ω1 принимать 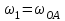 .
.
| Вариант | Исходные данные | Найти | |||||
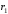 , м , м | 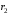 , м , м | 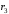 , м , м | 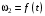 , ,1/с | 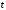 , с , с | Скорости | Ускорения | |
| 8 | 0,3 | 0,15 | 0,1 | 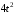 | 3,0 | 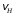 , , 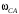 | 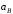 , , 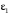 |
Решение
1. Определяем скорость точки Н.
Механическая система состоит из четырёх тел, совершающие следующие движения: тело 1 неподвижно, к нему присоединено водило ОАВ, вращающееся вокруг оси, проходящей через точку О, колесо 2 с двумя ободами, шатун АС, совершающий плоское движение, и ползун С, который перемещается поступательно вдоль своих направляющих.
Чтобы найти скорость точки Н
 необходимо знать угловую скорость тела 2
необходимо знать угловую скорость тела 2 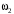 , которому принадлежит эта точка, и положение МЦС тела 2. Угловая скорость
, которому принадлежит эта точка, и положение МЦС тела 2. Угловая скорость 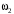 задана в условии задачи. МЦС тела 2 будет находиться в точке контакта поверхностей тела 1 и 2 – точке
задана в условии задачи. МЦС тела 2 будет находиться в точке контакта поверхностей тела 1 и 2 – точке 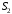 . Тогда искомая скорость точки Н будет равна
. Тогда искомая скорость точки Н будет равна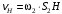 ,
,где
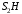 – расстояние от точки Н до МЦС
– расстояние от точки Н до МЦС 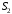 .
.Из треугольника
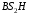 по теореме косинусов имеем
по теореме косинусов имеем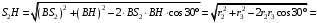
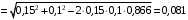 м.
м.Тогда
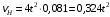 . (1)
. (1)Точка
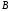 принадлежит колесу 2(3), поэтому ее скорость будет равна
принадлежит колесу 2(3), поэтому ее скорость будет равна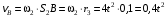 .
.Точка В принадлежит также водилу ОАВ, которое вращается с угловой скоростью
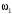 вокруг оси, проходящей через точку О. Следовательно,
вокруг оси, проходящей через точку О. Следовательно,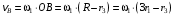 ,
,откуда найдем угловую скорость водила
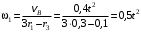 .
.2. Определение угловой скорости шатуна
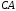
 .
.Для определения угловой скорости
 необходимо знать скорость какой-либо точки звена
необходимо знать скорость какой-либо точки звена 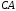
и положение его мгновенного центра скоростей
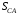 . Такой точкой является точка А, которая лежит в середине водила и скорость которой равна
. Такой точкой является точка А, которая лежит в середине водила и скорость которой равна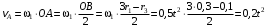 .
.Направлен вектор скорости
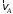 перпендикулярно отрезку ОА в сторону вращения кривошипа (рис.3).
перпендикулярно отрезку ОА в сторону вращения кривошипа (рис.3).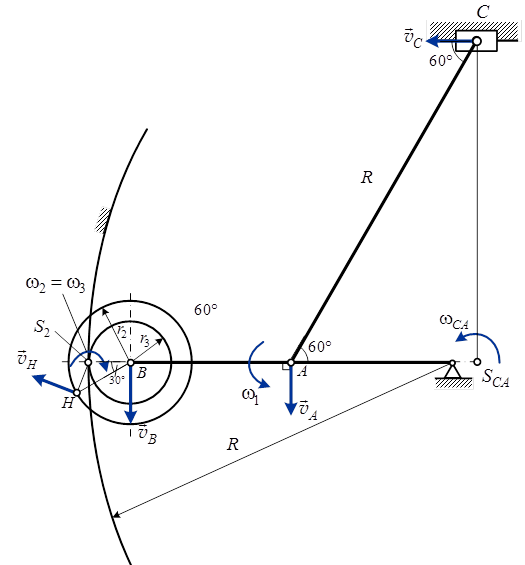
Рис.3. Расчетная схема для определения скоростей и ускорений
Далее рассмотрим точку С. Эта точка принадлежит шатуну СА, угловую скорость которого надо определить. Она же принадлежит одновременно ползуну
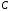 , который движется поступательно в горизонтальном направлении.
, который движется поступательно в горизонтальном направлении.Далее через точки A и С проведем прямые, перпендикулярные направлениям векторов скоростей
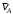 и
и 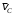 (
(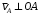 ,
, 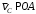 ) и на пересечении получим мгновенный центр скоростей стержня СА – точку
) и на пересечении получим мгновенный центр скоростей стержня СА – точку 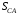 . Полученный треугольник
. Полученный треугольник 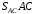 является прямоугольным, в котором отрезок
является прямоугольным, в котором отрезок 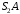 равен
равен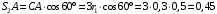 м.
м.Далее находим искомую угловую скорость звена СА:
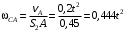 . (2)
. (2)3. Определяем ускорение точки
 согласно векторному уравнению
согласно векторному уравнению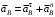 ,
,где его касательная и нормальная составляющие равны
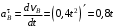 ;
;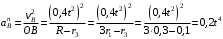 .
.Тогда
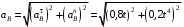 . (3)
. (3)4. Угловое ускорение
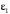 определим как
определим как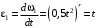 . (4)
. (4)Определив кинематические зависимости между точками и телами механической системы, найдем искомые величины при заданном моменте времени
