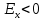Файл: Необходимо Вычислить выборочное среднее по первым 25 значениям, вычислить выборочное среднее по всему объему выборки. Сравнить.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 27.04.2024

Просмотров: 20

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задание 1.
Необходимо:

1. Вычислить выборочное среднее по первым 25 значениям, вычислить выборочное среднее по всему объему выборки. Сравнить.

2. Вычислить выборочную дисперсию по первым 25 значениям, вычислить выборочную дисперсию по всему объему выборки. Сравнить.

3. Рассчитать моду и медиану вариационного ряда (n=45).

4. Получить интервальный вариационный ряд по всему объему выборки, разделив выборочные значения на 5 интервалов.

5. Построить гистограмму. Сделать вывод.

6. Рассчитать выборочное среднее, выборочную дисперсию интервального вариационного ряда, моду и медиану.

7. Рассчитать коэффициент вариации, коэффициенты асимметрии и эксцесса и сделать вывод о характере распределения случайной величины Х. Пояснить результат.

8. Проверить, включает ли выборка аномальные значения (по правилу «трех сигм»). Сделать вывод по п.7 и 8.

9. Составить аналитическое заключение по заданию 1.
Решение.

Таблица 1. Исходные данные

№
X
№
X

1
1,19
26
1,11

2
0,92
27
0,84

3
0,87
28
1,04

4
0,83
29
0,86

5
0,98
30
0,81

6
1,18
31
1,09

7
1,19
32
0,86

8
1,11
33
0,94

9
1,18
34
1,18

10
0,88
35
1,02

11
0,87
36
1,20

12
1,08
37
1,04

13
1,04
38
0,86

14
0,86
39
1,11

15
1,07
40
1,14

16
1,12
41
0,97

17
0,93
42
1,05

18
0,82
43
1,00

19
1,11
44
1,00

20
0,98
45
0,88

21
1,09






22
0,95






23
0,84






24
1,03






25
1,17







Х - результаты регистрации значений затухания сигнала xi на частоте 1000 Гц коммутируемого канала телефонной сети.
1. Вычислим выборочное среднее по первым 25 значениям и по всему объему выборки. Сравним.





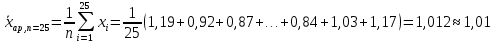
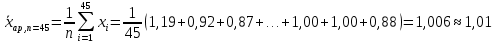
Можно считать, что значения выборочных средних по первым 25 значениям и по всему объему выборки (45 значений) близкие между собой значения.

2. Вычислим выборочную дисперсию по первым 25 значениям и выборочную дисперсию по всему объему выборки. Сравним.




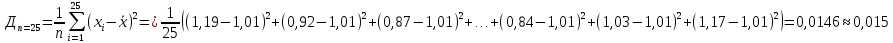
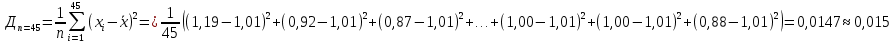
Можно считать, что значения выборочных дисперсий по первым 25 значениям и по всему объему выборки (45 значений) близкие между собой значения.

3. Рассчитаем моду и медиану вариационного ряда (n=45).

Ранжируем исходный ряд (Таблица 2)

Таблица 2

№
X
№
X

1
0,81
26
1,04

2
0,82
27
1,04

3
0,83
28
1,05

4
0,84
29
1,07

5
0,84
30
1,08

6
0,86
31
1,09

7
0,86
32
1,09

8
0,86
33
1,11

9
0,86
34
1,11

10
0,87
35
1,11

11
0,87
36
1,11

12
0,88
37
1,12

13
0,88
38
1,14

14
0,92
39
1,17

15
0,93
40
1,18

16
0,94
41
1,18

17
0,95
42
1,18

18
0,97
43
1,19

19
0,98
44
1,19

20
0,98
45
1,2

21
1






22
1






23
1,02






24
1,03






25
1,04






Медиана 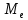– это значение признака, приходящегося на середину ранжированного ряда наблюдений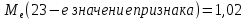



Мода 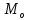– это значение признака, которое наблюдалось наибольшее число раз.

,

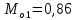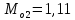
4. Построим интервальный вариационный ряд по всему объему выборки, разделив выборочные значения на 5 интервалов (таблица 3).



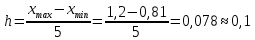
Таблица 3

Частичный интервал длиною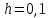

Сумма частот вариант частичного интервала,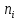

Плотность частоты,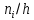

0,76
0,86
5
50,0

0,86
0,96
12
120,0

0,96
1,06
11
110,0

1,06
1,16
10
100,0

1,16
1,26
7
70,0

 
 
45
 


5. Построим гистограмму (рис.1).



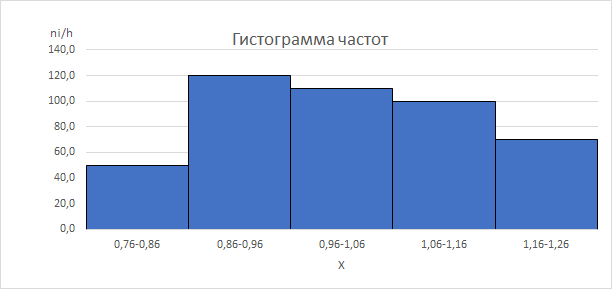
Рис.1

Гистограмма имеет одновершинную форму, можно предположить, что выборочная совокупность однородна, т.е. среднее значение типично для данной совокупности. Характер «затухания» для малых и больших значений не одинаков, распределение не симметрично.

6. Рассчитаем выборочное среднее, выборочную дисперсию интервального вариационного ряда, моду и медиану.

Составим расчетную таблицу 4.


Таблица 4

Xi
fi
Накопленные частоты
Середина интервала, Xи
Xиfi
(Xи-Xср)2fi
(Xи-Xср)3fi
(Xи-Xср)4fi

0,76
0,86
5
5
0,81
4,05
0,209
-0,043
0,009

0,86
0,96
12
17
0,91
10,92
0,131
-0,014
0,001

0,96
1,06
11
28
1,01
11,11
0,000
0,000
0,000

1,06
1,16
10
38
1,11
11,1
0,091
0,009
0,001

1,16
1,26
7
45
1,21
8,47
0,268
0,052
0,010

Сумма
45
 



45,65
0,699
0,005
0,021









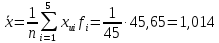
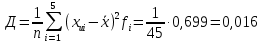
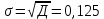
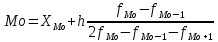
где ХMo– нижнее значение модального интервала;

fMo – число наблюдений в модальном интервале;

fMo-1 – то же для интервала, предшествующего модальному;

fMo+1 – то же для интервала, следующего за модальным;

h – величина интервала.





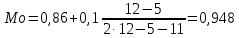
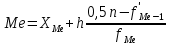
где XMe – нижняя граница медианного интервала;

h –величина интервала;

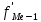– сумма наблюдений, накопленная до начала медианного интервала;

fMe – число наблюдений в медианном интервале.

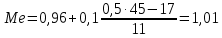
7. Рассчитаем коэффициент вариации, коэффициенты асимметрии и эксцесса и сделаем вывод о характере распределения случайной величины Х.

Коэффициент вариации:



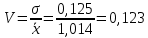
Так как 0,123 <0,333, то можно сделать вывод об однородности совокупности и о типичности среднего значения для данного набора данных.

Коэффициент асимметрии:



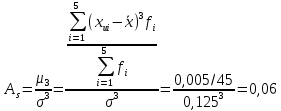
Значение коэффициента асимметрии положительно, значит в ряду преобладают варианты, которые больше средней (правосторонняя скошенность).

Коэффициент эксцесса:



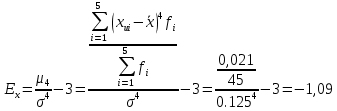
Так как 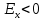, то распределение низковершинное.

Коэффициент 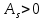, значит распределение имеет правостороннюю асимметрию. Коэффициент

Смотрите также файлы