Файл: Тесты к экзамену по учебной дисциплине " Математика ".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕСТЫ К ЭКЗАМЕНУ
по учебной дисциплине
"Математика "
ДВОЙНЫЕ ИНТЕГРАЛЫ
Составитель доц. Брылевская Л.И.
Для специалистов
Санкт-Петербург
2013
Двойные интегралы (для специалистов) | ||
КАТЕГОРИЯ 1 | ||
| № | Вопрос | Варианты ответа |
| | Какая сумма является интегральной для функции |
4. |
| | Двойной интеграл | 1. Ординате центра тяжести плоской пластины D. 2. Массе неоднородной пластины D . 3. Площади области D. 4. Абсциссе центра тяжести плоской пластины D. |
| | Двойным интегралом от функции f (x,y) по замкнутой области Dназывается |
4. Конечный предел интегральной суммы при условии |
| | Если функции | 1. 2. 3. 4. |
| | Если для функции 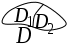 | 1. 0. 2. - 3 3. 6. 4. 13 |
| | Двойной интеграл |
3. 8 4. 2 |
| | Значение интеграла | 1. 0,5y2. 2. -1 3. 0 4. 2 |
| | Повторный интеграл 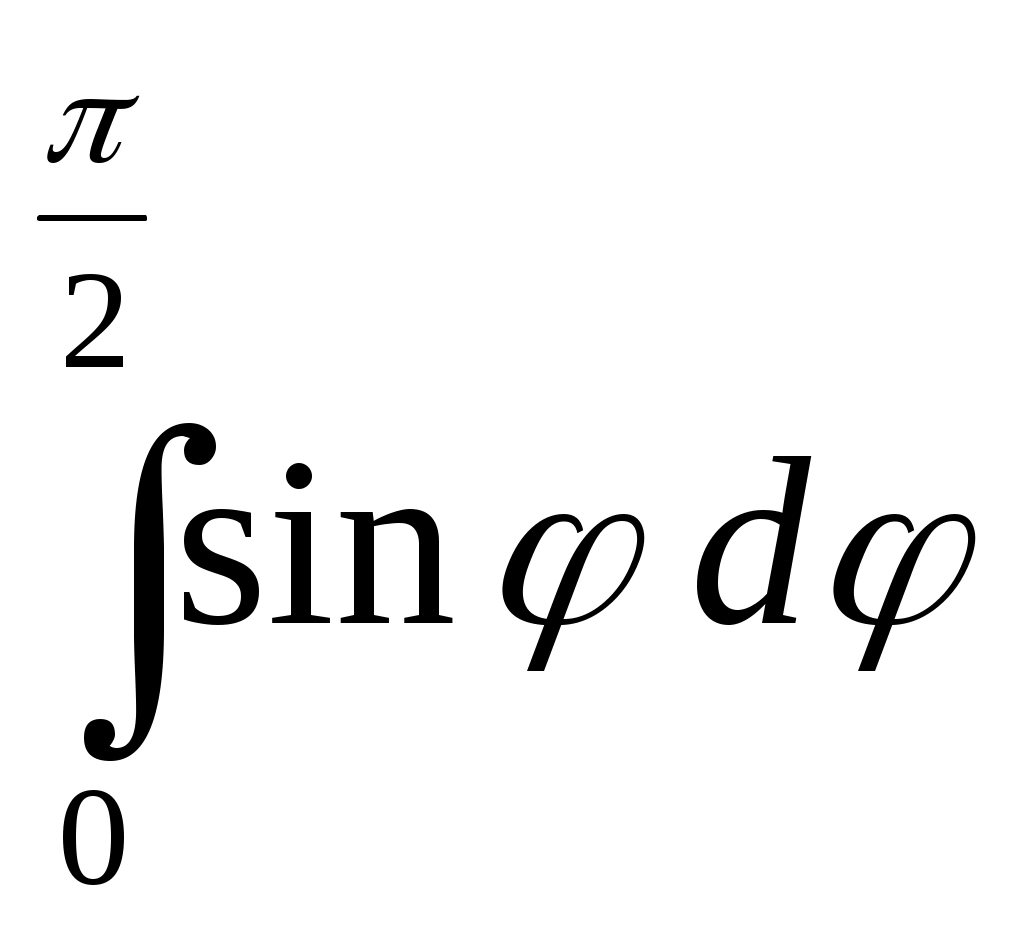 | 1. - 2. 1 3. 0 4. |
| | Какому повторному интегралу по области равен двойной интеграл | 1. 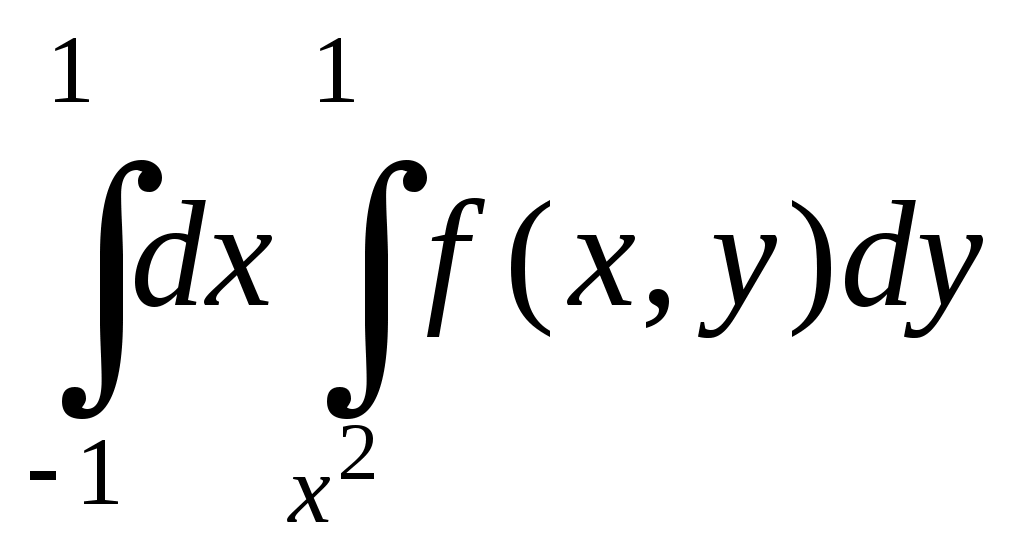 . .2. 3. 4. 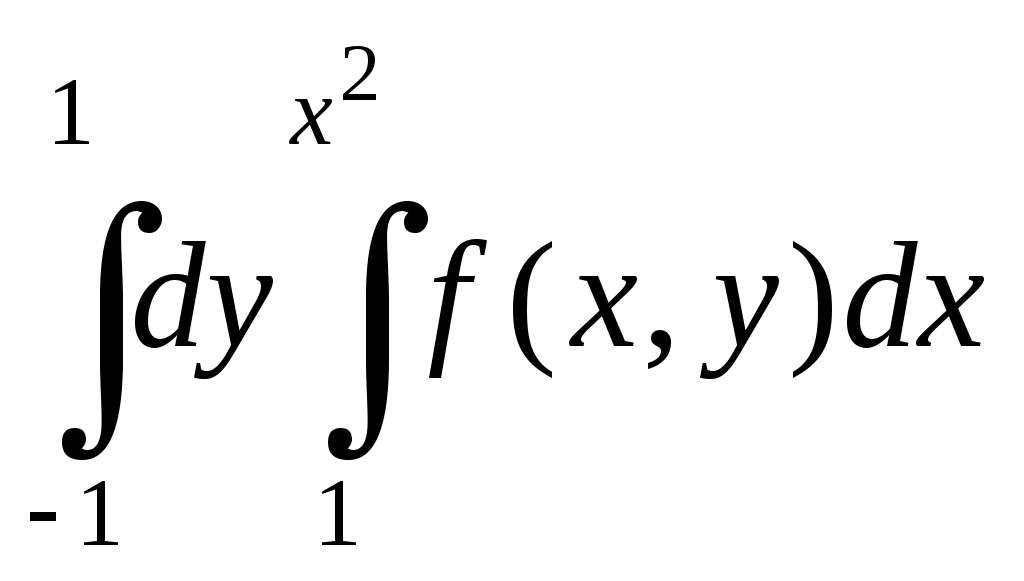 . . |
| | Если |
3. x = cos, y = sin. 4. x = sin, y = cos. |
| | Укажите, по какой формуле можно найти объем тела в полярной системе координат. | 3. 4. |
| | Указать формулу, определяющую массу плоской области |
3. 4. |
| | В интеграле | 1. 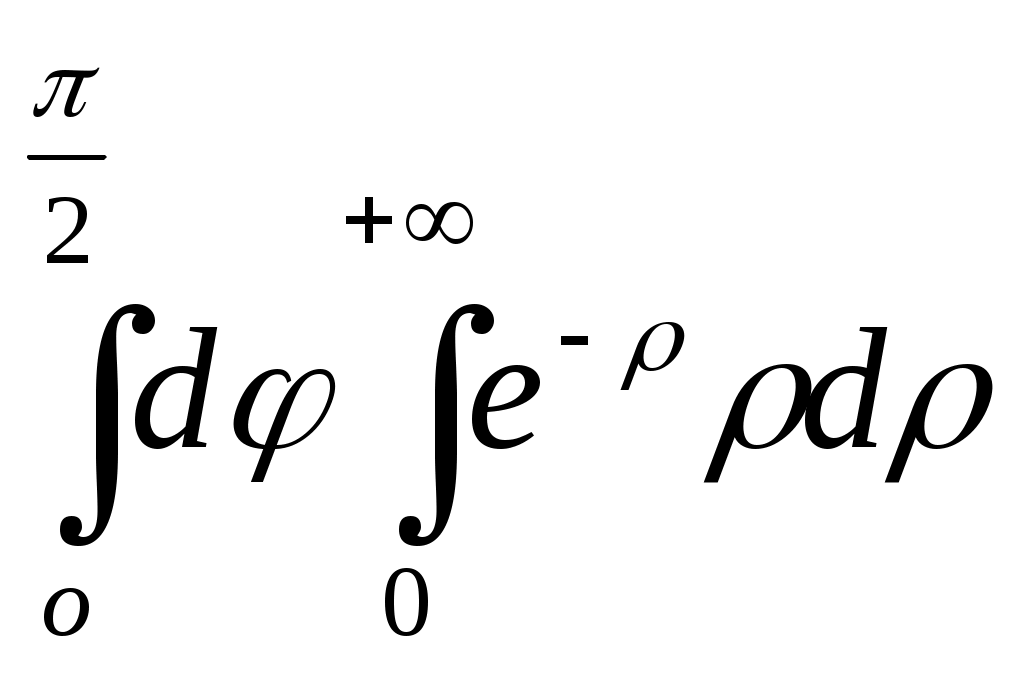 2. 2. 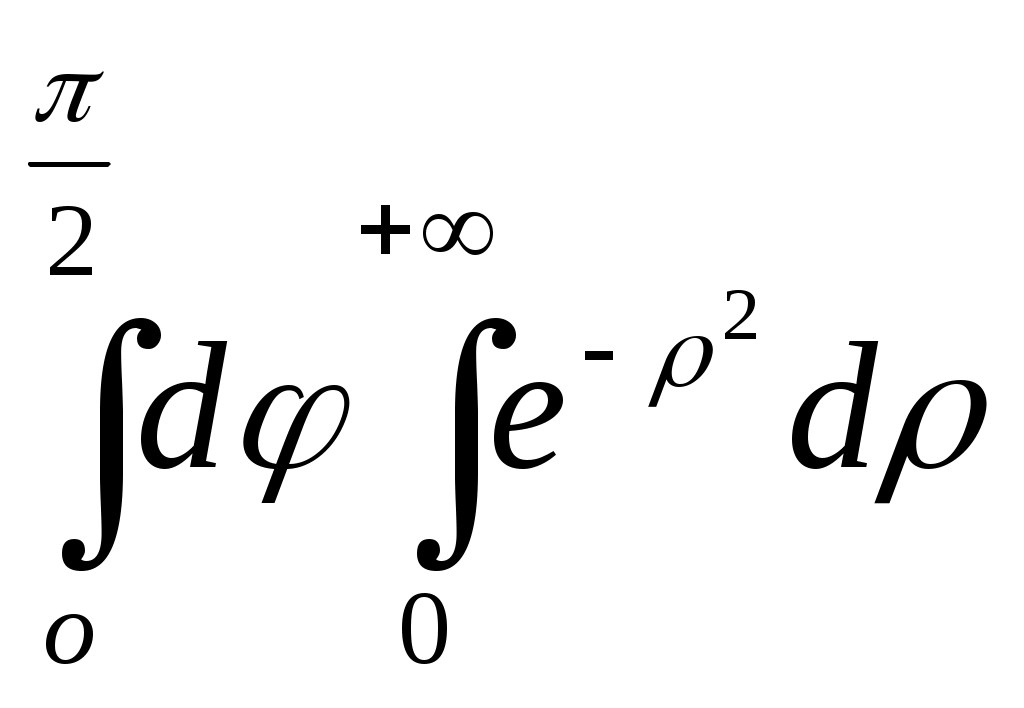 3.  4. 4. |
| | Значение интеграла | 1. 0 2. x 3. y 4. 1 |
| | Известно, что Чему будет равен объем цилиндрического тела с основанием D, образующими, параллельными оси Oz, и ограниченного сверху плоскостью | 1. 6π 2. 12π 3. 36 4. 6 |
| | Перейти в двойном интеграле к полярным координатам... | 1. 2. 3. 4. |
| 17. | Двойной интеграл задает … | 1. объем цилиндрического тела с основанием D и высотой 2; 2. массу неоднородной материальной пластины D с функцией плотности 3. центр тяжести материальной пластины D; 4. площадь поверхности, заданной функцией |
| 18. | Масса материальной пластины D, имеющей плотность, задаваемую непрерывной в D функцией | 1. 2. 3. 4. |
| 19. | Укажите значение двойного интеграла если область Dограничена прямыми | 1.1 2. 0,5 3. 4 4. 0,35 |
| 20. | Если для любых точек | 1. где 2. 3. 4. |
| 21. | На какое минимальное число областей второго типа можно разбить многоугольник АВСDЕ для нахождения интеграла 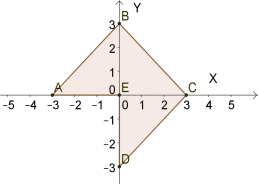 | 1. Многоугольник АВСDЕ нельзя разбить на области второго типа. 2. 3 3. 2 4. 6 |
| 22. | При переходе к полярным координатам получим следующий двукратный интеграл … | 1. 2. 3. 4. |
| 23. | Найдите значение двукратного интеграла | 1. -20 2. 0 3. -1 4. 12 |
| 24. | Если объем тела Т равен то проекция тела Т на плоскость ХОУ имеет форму … | 1. прямоугольника. 2. треугольника. 3. круга. 4. трапеции. |
| 25 | При переходе к полярным координатам интеграл | 1. 2. 3. 4. |
| 26 | При переходе к полярным координатам  | 1. 2. 3. 4. |
Двойные интегралы (для специалистов) | ||
КАТЕГОРИЯ 2 | ||
| № | Вопрос | Варианты ответа |
| 27 | Для двойного интеграла от любой непрерывной функции | 1. Найдется такая точка 2. 3.Найдется такая точка 4.Нет правильного ответа. |
| 28 | Двойной интеграл | 1. 2. 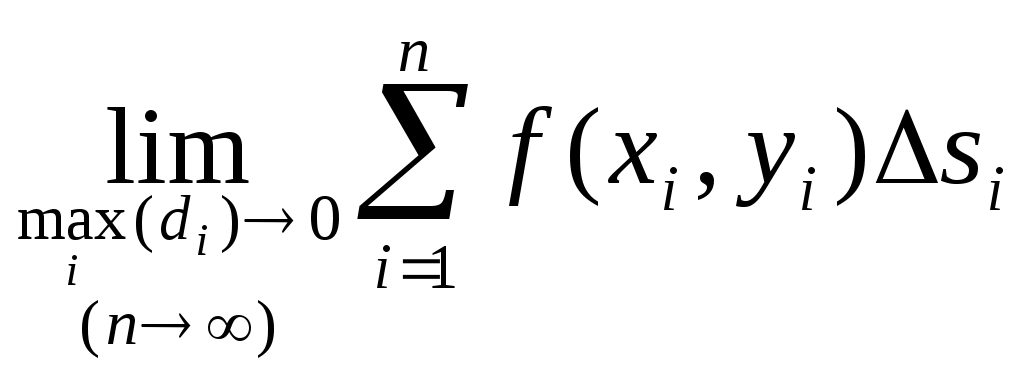 , где , где 3. 4. 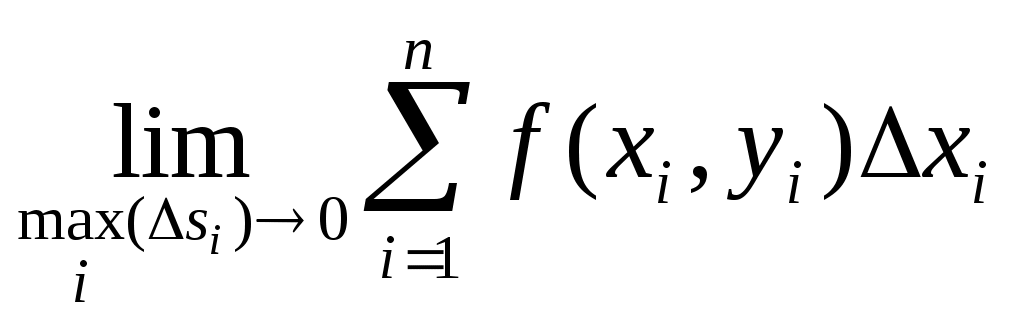 . . |
| 29 | Если пластинка занимает ограниченную область D плоскости хОу и имеет переменную плотность | 1. 2. 3. 4. |
| 30 | |
3. 4. |
| 31 | Если область D описана системой неравенств: |
3. 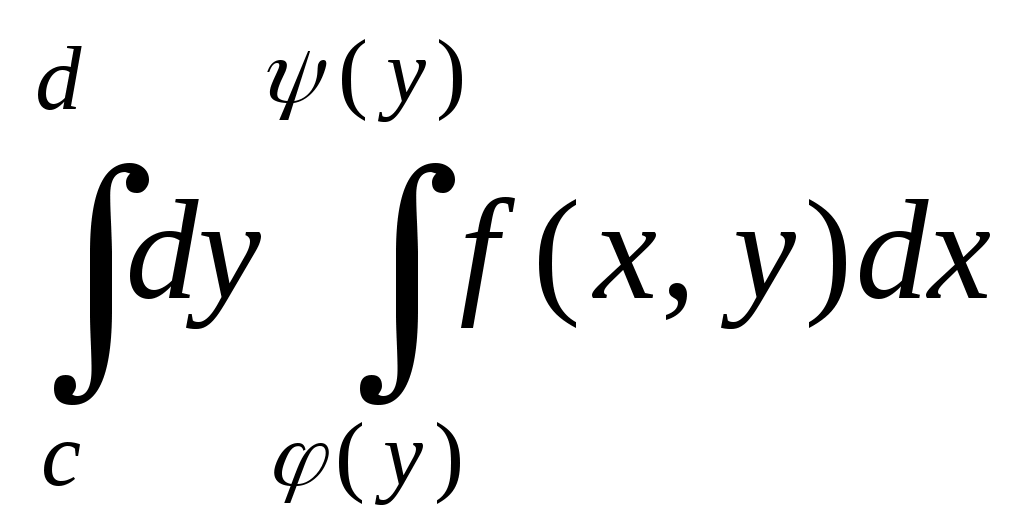 . .
|


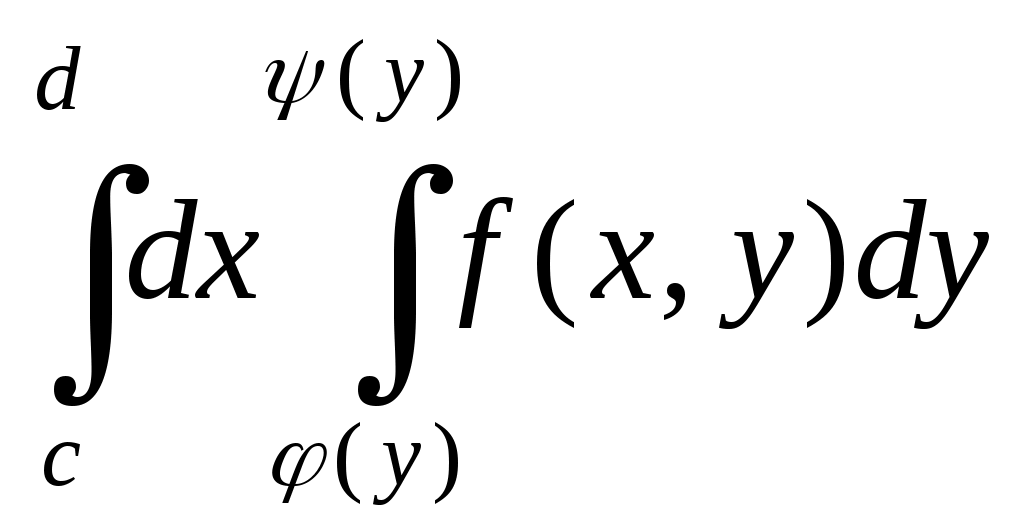 .
.