Файл: Тесты к экзамену по учебной дисциплине " Математика ".doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 27.04.2024

Просмотров: 17

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



32
Найдите значение интеграла
1.

2. 0

3. 1

4. -1

33
Какому повторному интегралу по области

равен двойной интеграл

  1. .

  2. .

3. .

4. .

34
Д войной интеграл по области D , приведенной на рисунке, равен:
1. .

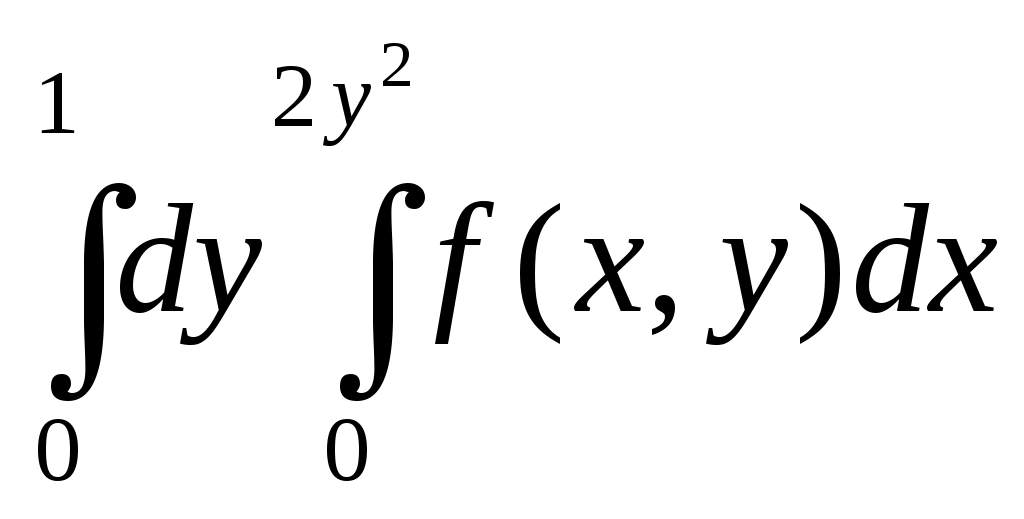2. .

3. .

4. .

35
Укажите формулу замены переменной в двойном интеграле, если I − якобиан преобразования, а -формулы перехода к новым переменным...







4.




36
Какие повторные интегралы по области ра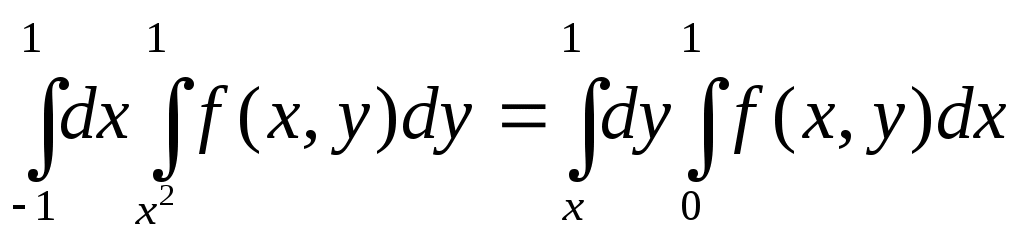вны?



2.

3.

4. .

37
Для тела, ограниченного поверхностями , его проекция наплоскость представляет собой
1. Треугольник

2. Эллипс

3. Круг

4. Прямоугольник


38
Двойной интеграл п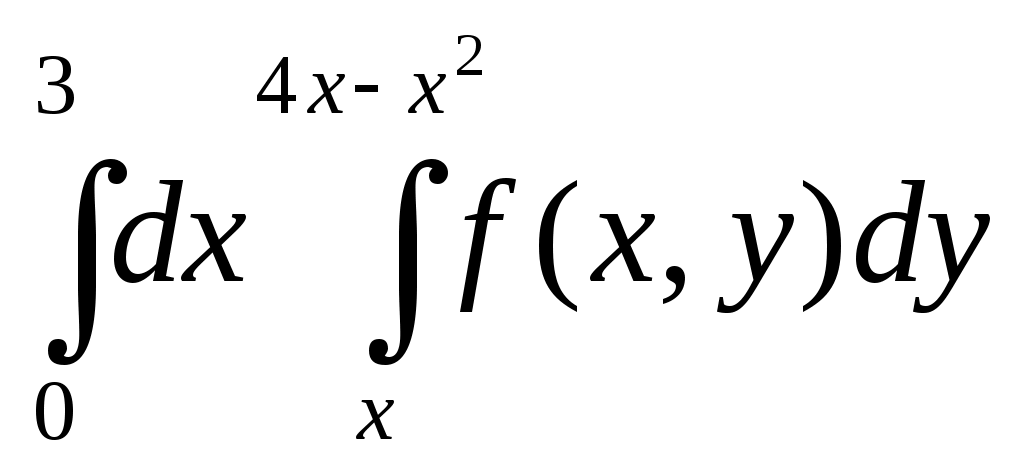о области равен
1.

2.

3.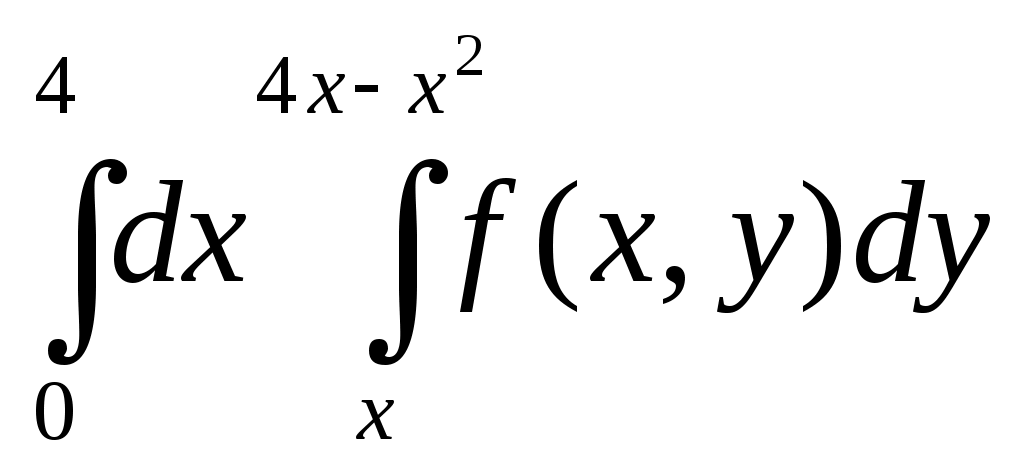

4.


39
Если двойной интеграл равен интегралу вида то область интегрирования − это...
1.Прямоугольник.

2.Круг

3.Невозможно определить.

4.Квадрат.



40
У кажите, какому из повторных интегралов равен двойной интеграл по области D, изображенной на чертеже.
1. ;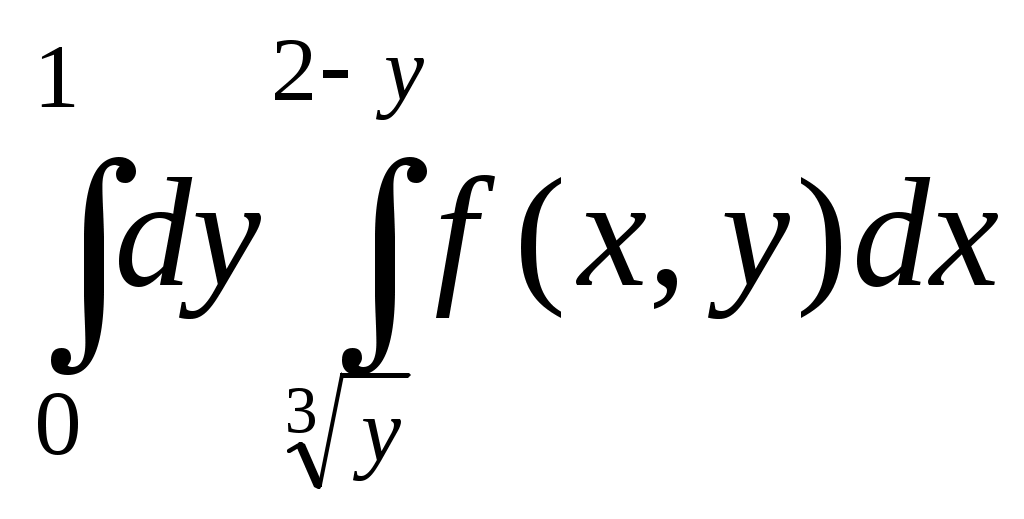

2. ;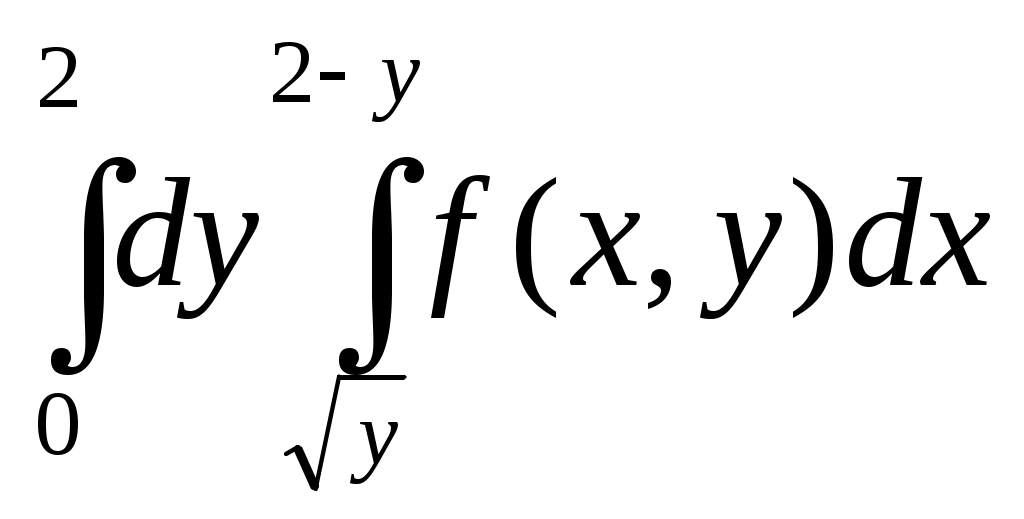

3. ;

4. .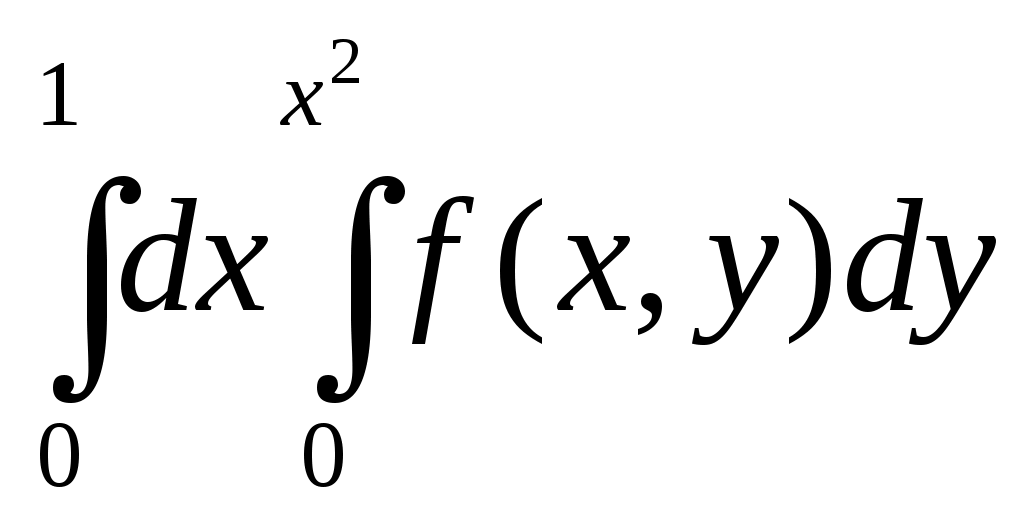

41
При перемене порядка интегрирования в повторном интеграле , получим......
1. ;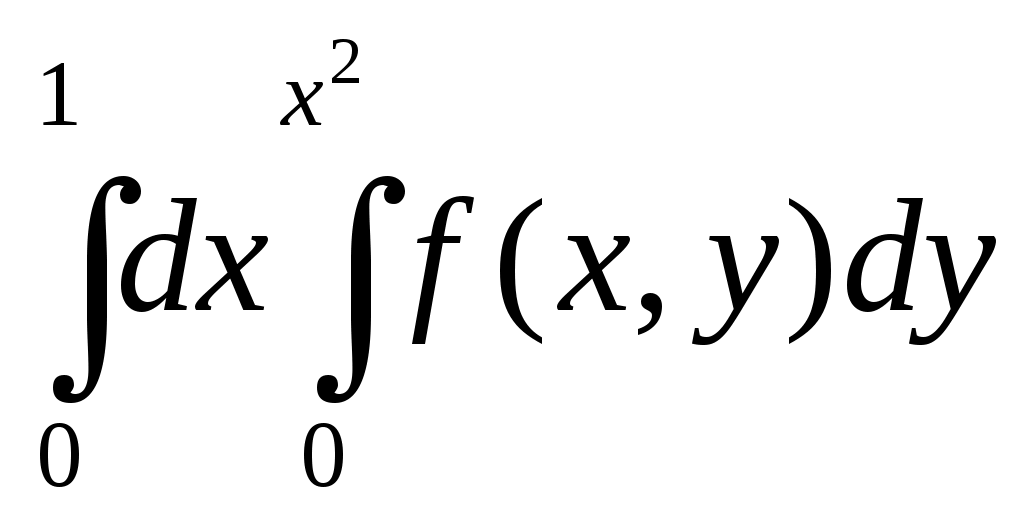

2. ;

3. ;

4. .

42
Какими поверхностями ограничено тело, если известно, что его объем в полярных координатах выражается интегралом

1. плоскостью и параболоидом

2. сферой радиуса с центром в начале координат и цилиндром

3. плоскостью и конусом

4. сферой радиуса с центром в начале координат и параболоидом





43
Координата це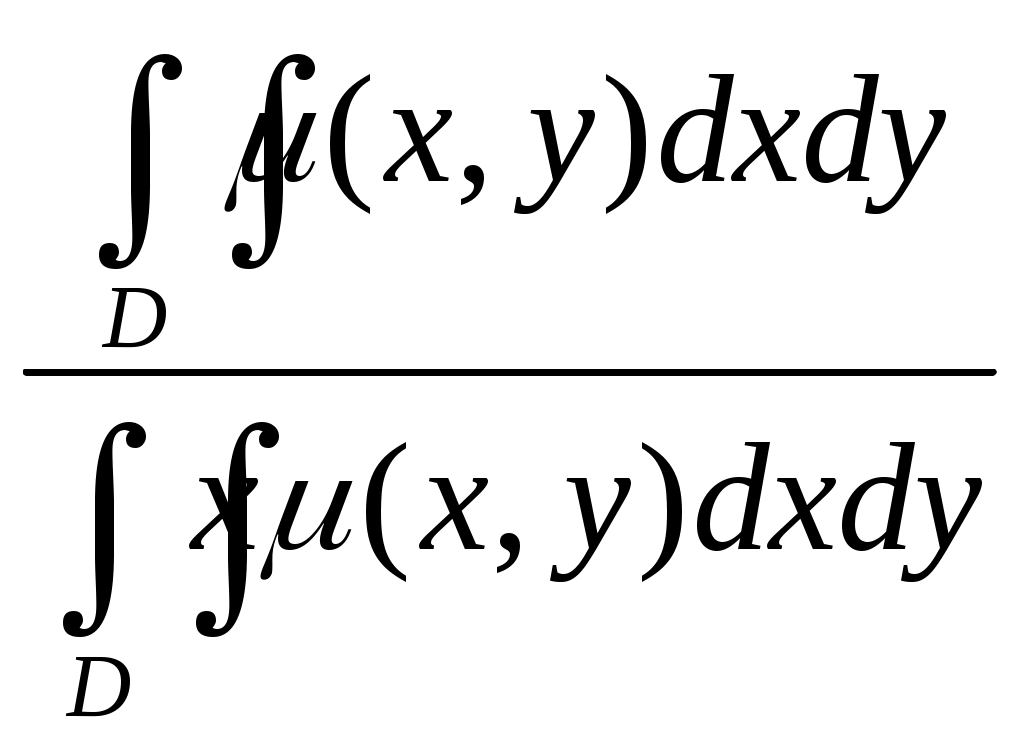нтра масс материальной пластины D, имеющей непрерывную плотность , равна:
1.

2.

3.

4.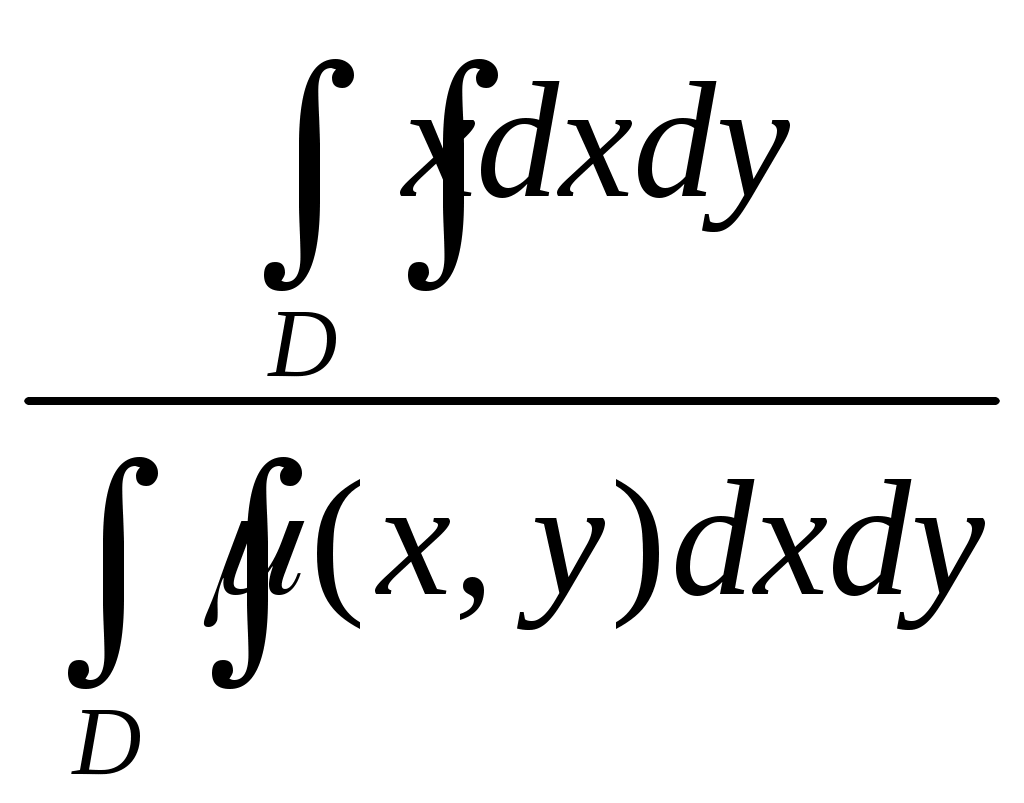

44
Дана непрерывно дифференцируемая в области D функция .

Интеграл

численно равен …
1. площади гладкой поверхности ,

заданной в области D.

2. объему цилиндрического тела с основанием D, образующими, параллельными оси Oz, и ограниченного поверхностью .

3. массе пластины D.

4.объему тела вращения, получаемого вращением поверхности вокруг оси Oz.

45
Непрерывная на ограниченной области D функция такова, что в любой точке области D . Какое из следующих утверждений верно?
1.

2.

3. интегральная сумма из определения двойного интеграла функции

по области D меньше 0.

4. интегральная сумма из определения двойного интеграла функции

по области D больше 0.



46
Если для любых точек из области D верно неравенство , то …
1. ,

где - площадь области D.

2.

3.

4.

47
На какое минимальное число областей первого типа можно разбить параллелограмм АВСD?
1.2

2. 3

3. 4

4. 5

48
При изменении порядка интегрирования

…
1.

2.

3.

4.



49
При переходе к полярным координатам двойной интеграл ,

по области D, изображенной на чертеже, равен …
1.

2.

3.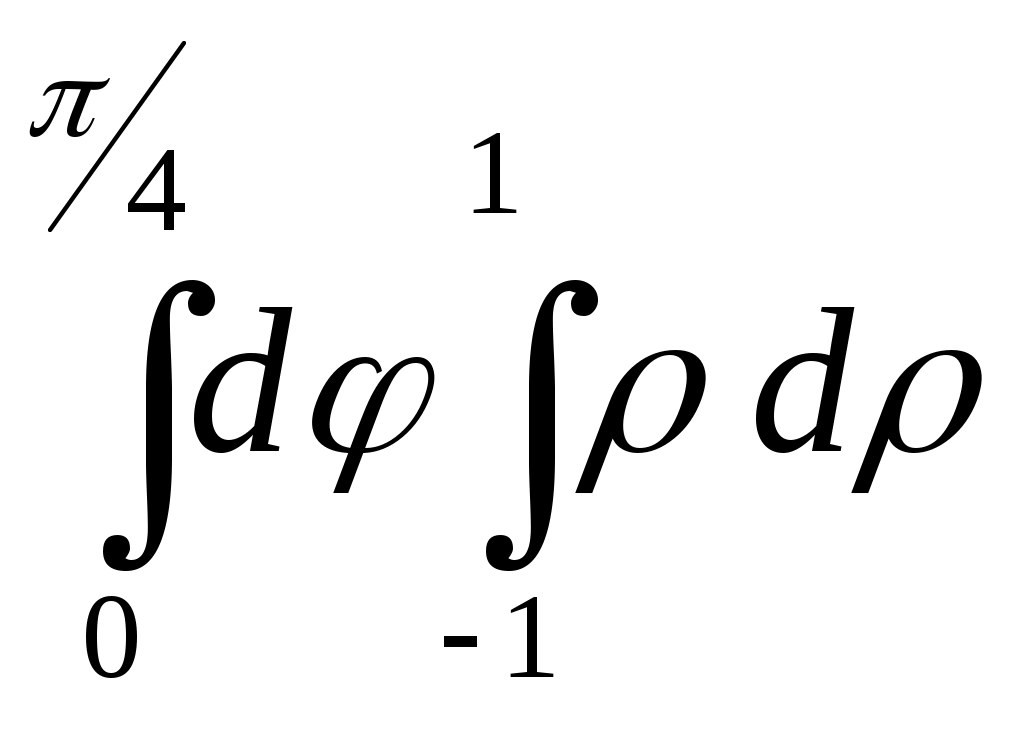

4.

50
Если площадь D области равна ,

то область D имеет форму …
1. прямоугольника.

2. треугольника.

3. круга.

4. трапеции.

51
Если двойной интеграл

равен интегралу вида , то область интегрирования − это..

  1. Ромб

  2. Прямоугольник.

  3. Квадрат.

4. Круг

52
Если объем тела Т равен ,

то проекция тела Т на плоскость ХОУ имеет форму …
1. прямоугольника.

2. треугольника.

3. круга.

4. трапеции

Смотрите также файлы