ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 32
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 параметр рассеивания годной продукции и через 1 – негодной. Их отношение =1/0 называют расстоянием между конкурирующими гипотезами (т.е. между гипотезой Н0: т.е. =0 и альтернативной гипотезой Н1: т.е. =1). Последовательность проверки гипотезы следующая. Берётся независимая выборка х1,…,хn и по ней находится оценка ( х1,…,хn), например х2 по уравнению (1). Задается критическое значение кр, соответствующее заданному уровню значимости (т.е. риску поставщика) и определяющее критическую область проверки гипотезы Н0: кр=, где – точка оперативной характеристики: ()=1–F(). Если выборочная точка попадает в критическую область, то отвергаем гипотезу Н0 и принимаем альтернативную гипотезу Н1. Имеем:
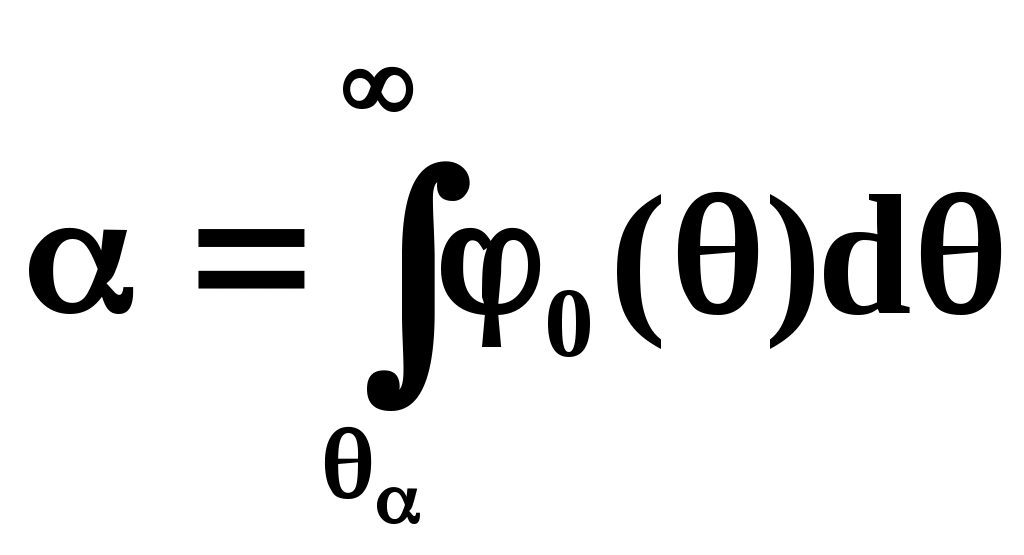(2)
Определим риск заказчика:
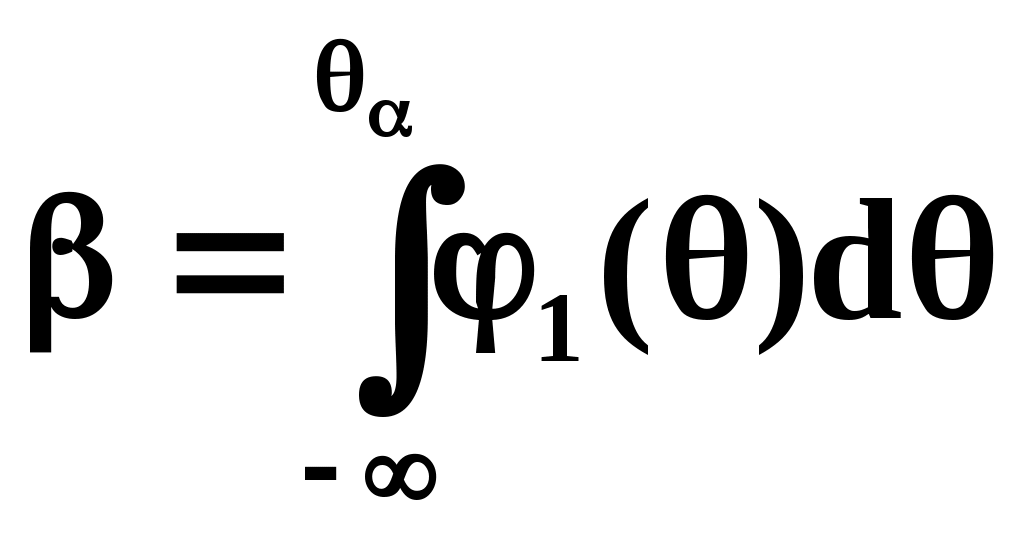(3)
Если плотности распределения подобны, то:
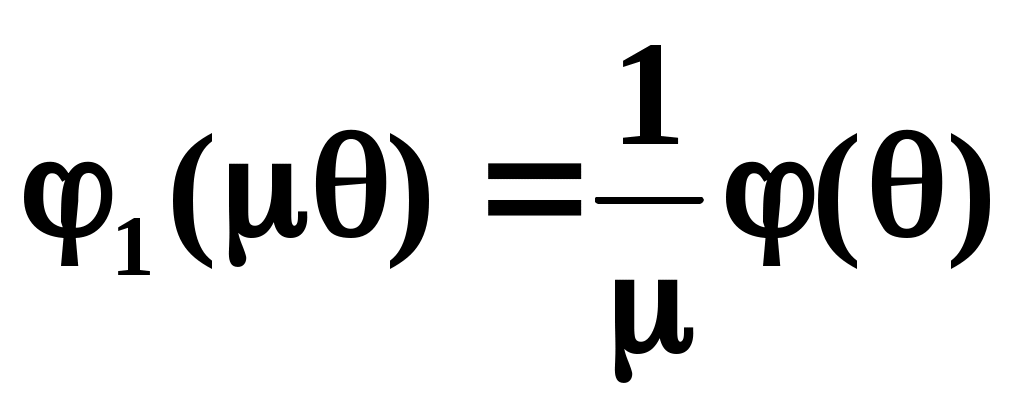(4)
где =/1– (5)
Риск поставщика (т.е. уровень значимости, или вероятность ошибки I-го рода) – это вероятность забраковать годную продукцию. Риск заказчика (т.е. вероятность ошибки II-го рода) – это вероятность принять негодную продукцию. Для пояснения вышесказанного сделаем рис:
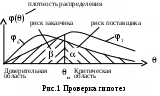
На данном рис. вероятности , соответствуют заштрихованным площадям под плотностями распределения. Видно противоречие между рисками. Чтобы уменьшить риск поставщика , нужно сместить границу критической области вправо, но при этом возрастёт риск заказчика . Чем больше расстояние между конкурирующими гипотезами , тем больше разнесены друг от друга на рис.1 кривые 0() и 1(). Соответственно обеспечиваются меньшие риски поставщика и заказчика. Следовательно, чем меньше
и при фиксированном , тем лучше, эффективнее оценка. Или чем меньше при фиксированных и , тем лучше оценка, или гипотезы более различимы. В случае точечного оценивания (например, номинальной величины сопротивления в парии резисторов) оценка тем лучше (т.е. эффективнее), чем меньше её дисперсия. Таким образом, логично использовать оценку, которая даёт: 1) ()=min; или 2) ()=min.
Такую оценку назовём оптимальной в первом или втором смысле (т.е. по дисперсии или по расстоянию). Переход к оптимальным оценкам по критериям минимума дисперсии или расстояния между конкурирующими гипотезами – позволяет уменьшить объём выборок или повысить достоверность и точность оценок и контроля при фиксированном объёме выборок. А эффективность оценок – это предмет теории вероятностей и мат. статистики.
Критерии согласия
Для проверки гипотезы о соответствии эмпирического и теоретического распределений применяют так называемые критерии согласия Пирсона, Колмогорова и другие. Наиболее мощный из них критерий 2 (хи-квадрат) был предложен Пирсоном в 1903г. и полностью разработан Фишером. Рассмотрим этот критерий более подробно.
В мат. статистике иногда вместо МНК используется метод максимального правдоподобия. При этом доказывается, что если погрешности распределены по нормальному закону, то оба метода дают одинаковые решения. В экспериментальных исследованиях чаще применяют МНК, особенно, в той его форме, когда при минимизации используются данные об экспериментальных ошибках. Такой метод называется 2 -квадрат (хи-квадрат).
Поиск аналитической зависимости с помощью метода 2 -квадрат
В МНК для нахождения неизвестных коэффициентов полинома необходимо выполнить условие. Это минимум квадратичной формы вида:
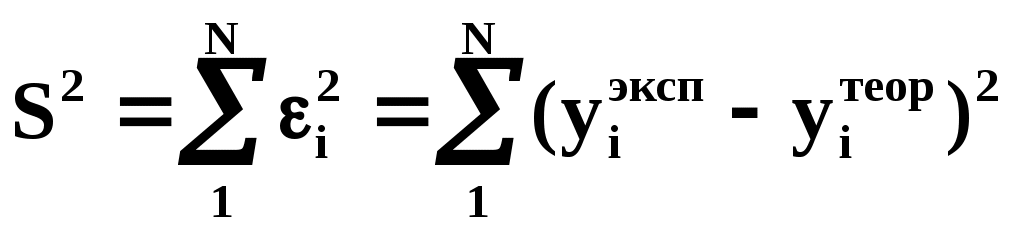(1)
В методе -квадрат используется несколько иная квадратичная форма, называемая функцией -квадрат:
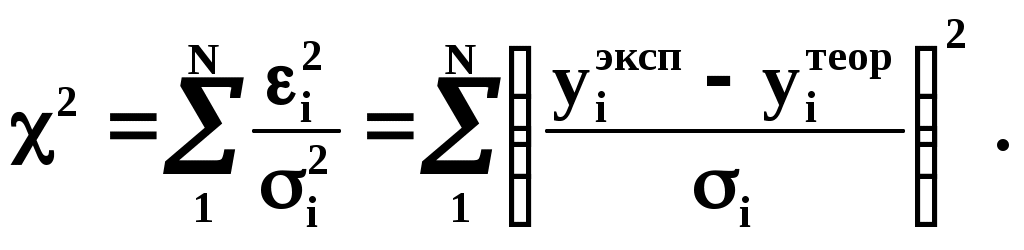(2)
Это выражение имеет больший физический смысл. Оно является безразмерной величиной и равно сумме квадратов отклонений экспериментальных точек от теоретической кривой в долях среднеквадратической ошибки.
Рассмотрим простейший случай, когда во всех измерениях одна и та же квадратическая ошибка (т.е. i=const). Тогда i в (2) можно вынести за знак суммы. При этом под знаком суммы оказываются те же выражения, что и в МНК. И будут получены те же значения коэффициентов искомой аналитической зависимости.
Рассмотрим, какую новую информацию даёт использование в этом случае.
При условии, что закон распределения ошибок i нормальный, сумма
подчиняется закону
2-распределения с k-степенями свободы. Число k-степеней свободы – это уменьшенное на единицу число измерений (т.е. точек) N за вычетом числа r определяемых коэффициентов аналитической зависимости: k=N-1-r.
Известно аналитическое выражение для теоретического распределения f(2):
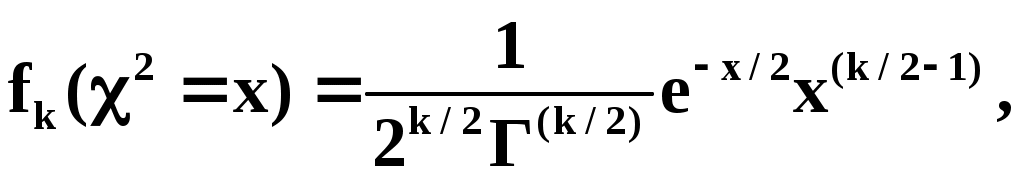
где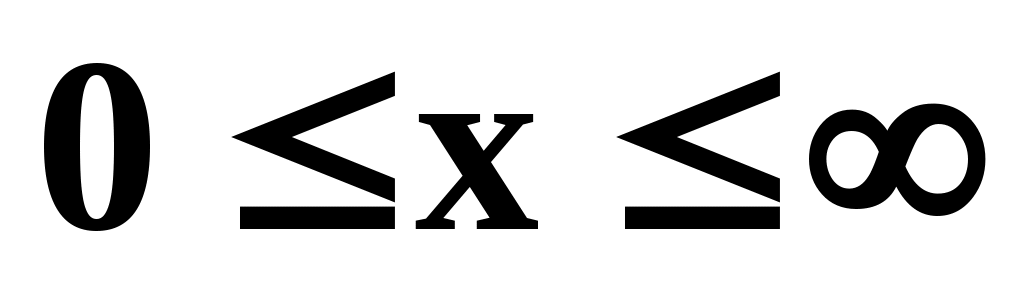
; Г(k/2) – так называемая Г-функция. Нарисуем график функции 
:
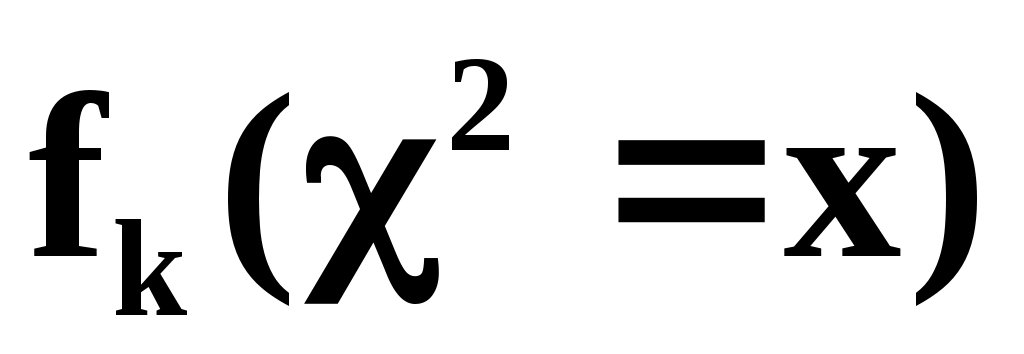Начиная с k=2, функция fk имеет максимум при x=k-2. При k2 распределение описывается несимметричной функцией, причём fk=0 при x=0 и fk0 при x.
Интеграл типа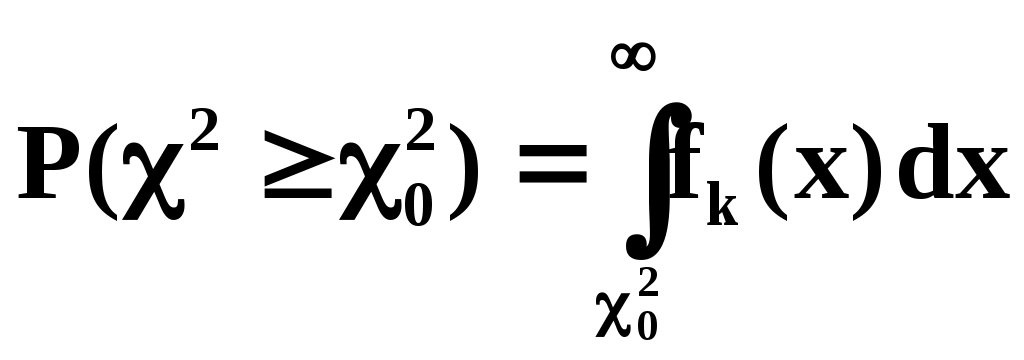
приводится в справочниках.
Рассмотрим пример пользования таблицей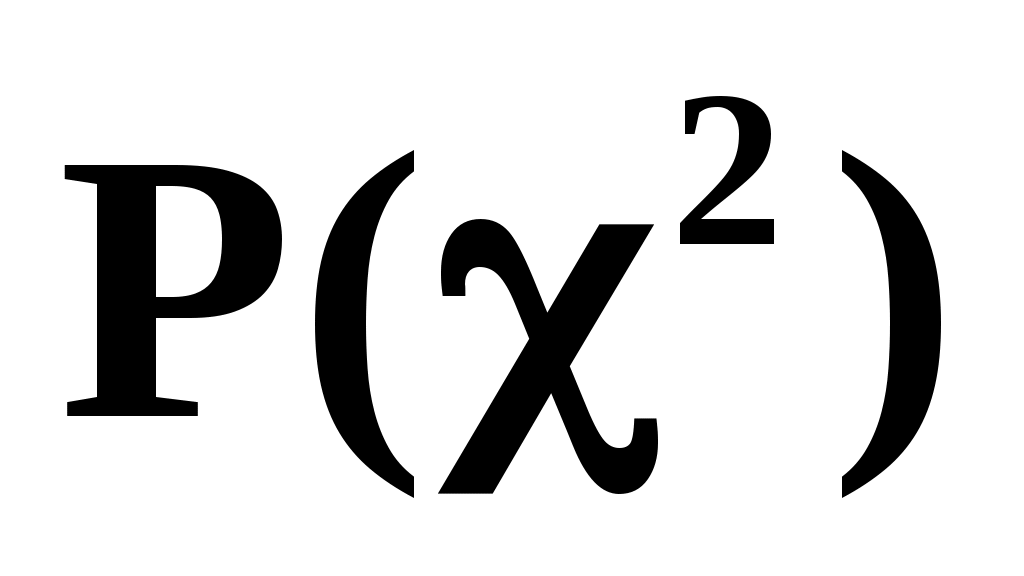
. Пусть число измерений равно 20. экспериментальные данные предполагается описать линейной зависимостью y=a+bx, для идентификации которой необходимо определить два параметра a и b. В рассматриваемом случае число степеней свободы равно:
k=20-1-2=17.
Предположим, что в результате расчётов по формуле (2) получили 2=12. Из таблицы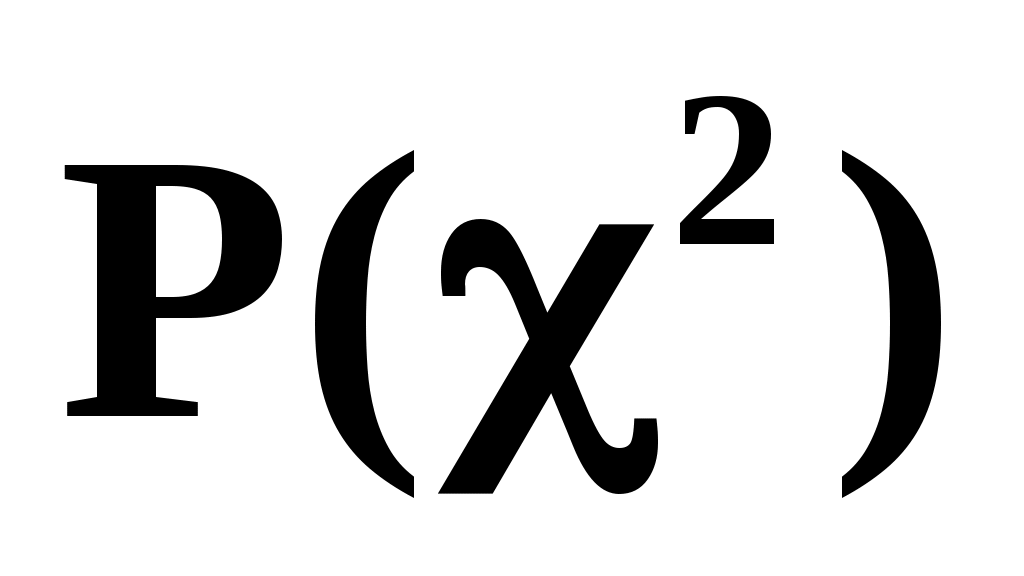 можно найти, что при 17 степенях свободы вероятность получить 212 составляет 80%. Иногда словами, такое или большее значение должно наблюдаться более, чем в 80% случаев.
При сравнении данных с таблицей применяют следующую терминологию. Если данные и большее значение 2 должны наблюдаться с вероятностью между 1 и 5%, то отклонения называют почти значимыми. Если вероятность меньше 0,1%, то отклонения являются высокозначимыми. При вероятности более 5% считают, что экспериментальные данные недостаточны, чтобы отвергнуть гипотезу.
Если бы в данном примере было получено 2=40, то вероятность получить 240 была бы 0,1%. Следовательно, можно было бы утверждать, что с помощью прямолинейной зависимости нельзя описать имеющийся набор экспериментальных данных.
Рассмотрим 7-й и последний этап построения модели.
ПРОВЕРКА УСЛОВИЙ КОНЦА
ЭКСПЕРИМЕНТА
На этом этапе проверяется соответствие модели критерию практики, т.е. проводятся проверка достоверности и оценка модели.
По Шеннону Роберту оценка модели делится на три категории.
1. Верификация (т.е. проверка), показывающая, что модель ведёт себя так как задумано.
2. Оценка адекватности – т.е. проверка соответствия между поведением модели и объекта, другими словами оценка точности.
3. Проблемный анализ – т.е. формулирование статистически значимых выводов на основе полученных данных. Это есть анализ и интерпретация полученных данных.
Отметим, что практическое использование построенной модели должно начинаться после её тщательной проверки и верификации. Верификация модели необходима для выявления и устранения ошибок, и заключается в проверках правильности арифметических и алгебраических действий, выводов уравнений модели и физического смысла полученных результатов. Можно выделить несколько аспектов проверки физического смысла.
Первый. В случае числовых результатов проверка заключается в соответствии полученных значений реальным значениям. При проверке правильности формул и уравнений прежде всего появляется непротиворечивость выражения с точки зрения физической размерности. Эта проверка настолько важна, что должна стать привычной для разработчика модели.
Второй аспект – это проверка пределов и ответ на вопрос, даёт ли полученное уравнение правильные результаты, если различные параметры и величины поочерёдно устремлять к некоторому пределу, например, к нулю, к бесконечности или некоторому граничному значению.
Третий аспект – это проверка тренда, т.е. тенденции изменения. Для проверки физического смысла совсем необязательно устремлять параметры и величины к какому-нибудь конкретному пределу. Можно просто представить, что они возрастают или убывают, и проверить изменения других величин с ожидаемыми изменениями. В частности, необходимо проверить, дополняют ли друг друга факторы, которые должны оказывать одинаковые воздействия, иначе говоря, влияют ли они на результат в одинаковом направлении. Однако наиболее важный этап
(2)Определим риск заказчика:
(3)Если плотности распределения подобны, то:
(4)где =/1– (5)
Риск поставщика (т.е. уровень значимости, или вероятность ошибки I-го рода) – это вероятность забраковать годную продукцию. Риск заказчика (т.е. вероятность ошибки II-го рода) – это вероятность принять негодную продукцию. Для пояснения вышесказанного сделаем рис:
На данном рис. вероятности , соответствуют заштрихованным площадям под плотностями распределения. Видно противоречие между рисками. Чтобы уменьшить риск поставщика , нужно сместить границу критической области вправо, но при этом возрастёт риск заказчика . Чем больше расстояние между конкурирующими гипотезами , тем больше разнесены друг от друга на рис.1 кривые 0() и 1(). Соответственно обеспечиваются меньшие риски поставщика и заказчика. Следовательно, чем меньше
и при фиксированном , тем лучше, эффективнее оценка. Или чем меньше при фиксированных и , тем лучше оценка, или гипотезы более различимы. В случае точечного оценивания (например, номинальной величины сопротивления в парии резисторов) оценка тем лучше (т.е. эффективнее), чем меньше её дисперсия. Таким образом, логично использовать оценку, которая даёт: 1) ()=min; или 2) ()=min.
Такую оценку назовём оптимальной в первом или втором смысле (т.е. по дисперсии или по расстоянию). Переход к оптимальным оценкам по критериям минимума дисперсии или расстояния между конкурирующими гипотезами – позволяет уменьшить объём выборок или повысить достоверность и точность оценок и контроля при фиксированном объёме выборок. А эффективность оценок – это предмет теории вероятностей и мат. статистики.
Критерии согласия
Для проверки гипотезы о соответствии эмпирического и теоретического распределений применяют так называемые критерии согласия Пирсона, Колмогорова и другие. Наиболее мощный из них критерий 2 (хи-квадрат) был предложен Пирсоном в 1903г. и полностью разработан Фишером. Рассмотрим этот критерий более подробно.
В мат. статистике иногда вместо МНК используется метод максимального правдоподобия. При этом доказывается, что если погрешности распределены по нормальному закону, то оба метода дают одинаковые решения. В экспериментальных исследованиях чаще применяют МНК, особенно, в той его форме, когда при минимизации используются данные об экспериментальных ошибках. Такой метод называется 2 -квадрат (хи-квадрат).
Поиск аналитической зависимости с помощью метода 2 -квадрат
В МНК для нахождения неизвестных коэффициентов полинома необходимо выполнить условие. Это минимум квадратичной формы вида:
(1)В методе -квадрат используется несколько иная квадратичная форма, называемая функцией -квадрат:
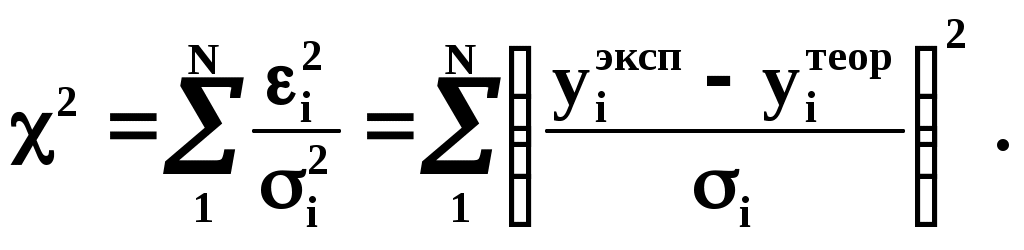(2)Это выражение имеет больший физический смысл. Оно является безразмерной величиной и равно сумме квадратов отклонений экспериментальных точек от теоретической кривой в долях среднеквадратической ошибки.
Рассмотрим простейший случай, когда во всех измерениях одна и та же квадратическая ошибка (т.е. i=const). Тогда i в (2) можно вынести за знак суммы. При этом под знаком суммы оказываются те же выражения, что и в МНК. И будут получены те же значения коэффициентов искомой аналитической зависимости.
Рассмотрим, какую новую информацию даёт использование в этом случае.
При условии, что закон распределения ошибок i нормальный, сумма
подчиняется закону
2-распределения с k-степенями свободы. Число k-степеней свободы – это уменьшенное на единицу число измерений (т.е. точек) N за вычетом числа r определяемых коэффициентов аналитической зависимости: k=N-1-r.
Известно аналитическое выражение для теоретического распределения f(2):
где
; Г(k/2) – так называемая Г-функция. Нарисуем график функции : Начиная с k=2, функция fk имеет максимум при x=k-2. При k2 распределение описывается несимметричной функцией, причём fk=0 при x=0 и fk0 при x.
Интеграл типа
приводится в справочниках.Рассмотрим пример пользования таблицей
. Пусть число измерений равно 20. экспериментальные данные предполагается описать линейной зависимостью y=a+bx, для идентификации которой необходимо определить два параметра a и b. В рассматриваемом случае число степеней свободы равно: k=20-1-2=17.
Предположим, что в результате расчётов по формуле (2) получили 2=12. Из таблицы
можно найти, что при 17 степенях свободы вероятность получить 212 составляет 80%. Иногда словами, такое или большее значение должно наблюдаться более, чем в 80% случаев.При сравнении данных с таблицей применяют следующую терминологию. Если данные и большее значение 2 должны наблюдаться с вероятностью между 1 и 5%, то отклонения называют почти значимыми. Если вероятность меньше 0,1%, то отклонения являются высокозначимыми. При вероятности более 5% считают, что экспериментальные данные недостаточны, чтобы отвергнуть гипотезу.
Если бы в данном примере было получено 2=40, то вероятность получить 240 была бы 0,1%. Следовательно, можно было бы утверждать, что с помощью прямолинейной зависимости нельзя описать имеющийся набор экспериментальных данных.
Рассмотрим 7-й и последний этап построения модели.
ПРОВЕРКА УСЛОВИЙ КОНЦА
ЭКСПЕРИМЕНТА
На этом этапе проверяется соответствие модели критерию практики, т.е. проводятся проверка достоверности и оценка модели.
По Шеннону Роберту оценка модели делится на три категории.
1. Верификация (т.е. проверка), показывающая, что модель ведёт себя так как задумано.
2. Оценка адекватности – т.е. проверка соответствия между поведением модели и объекта, другими словами оценка точности.
3. Проблемный анализ – т.е. формулирование статистически значимых выводов на основе полученных данных. Это есть анализ и интерпретация полученных данных.
Отметим, что практическое использование построенной модели должно начинаться после её тщательной проверки и верификации. Верификация модели необходима для выявления и устранения ошибок, и заключается в проверках правильности арифметических и алгебраических действий, выводов уравнений модели и физического смысла полученных результатов. Можно выделить несколько аспектов проверки физического смысла.
Первый. В случае числовых результатов проверка заключается в соответствии полученных значений реальным значениям. При проверке правильности формул и уравнений прежде всего появляется непротиворечивость выражения с точки зрения физической размерности. Эта проверка настолько важна, что должна стать привычной для разработчика модели.
Второй аспект – это проверка пределов и ответ на вопрос, даёт ли полученное уравнение правильные результаты, если различные параметры и величины поочерёдно устремлять к некоторому пределу, например, к нулю, к бесконечности или некоторому граничному значению.
Третий аспект – это проверка тренда, т.е. тенденции изменения. Для проверки физического смысла совсем необязательно устремлять параметры и величины к какому-нибудь конкретному пределу. Можно просто представить, что они возрастают или убывают, и проверить изменения других величин с ожидаемыми изменениями. В частности, необходимо проверить, дополняют ли друг друга факторы, которые должны оказывать одинаковые воздействия, иначе говоря, влияют ли они на результат в одинаковом направлении. Однако наиболее важный этап
