ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 34
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1=2=…=n=. Тогда нормальный закон, которому подчиняется величина Yi, можно записать в виде:
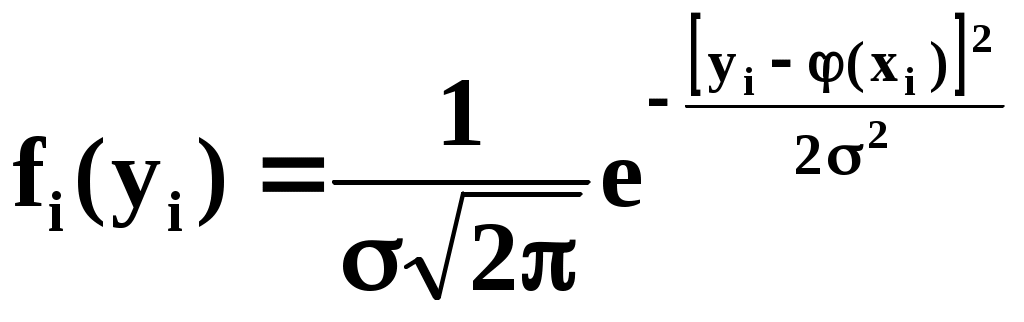
В результате нашего опыта (т.е. ряда измерений) произошло следующее событие: случайные величины (Y1,Y2,…,Yn) приняли совокупность значений (у1,у2,…,уn). Поставим задачу: так подобрать мат. ожидания (х1),(х2),…, (хn) чтобы вероятность этого события была максимальна (т.е. принцип максимального правдоподобия). Так как величины Yi непрерывны, то вероятность Yi=уi равна нулю. Поэтому будем пользоваться не вероятностями событий Yi=уi, а соответствующими элементами вероятностей:
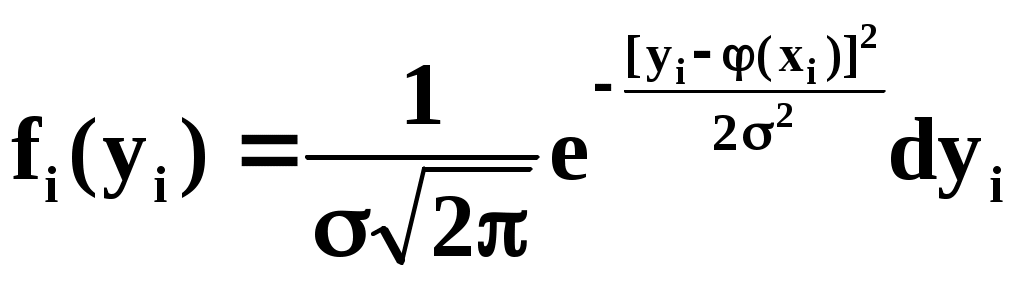 (1)
(1)
Найдём вероятность того, что система случайных величин Y1,Y2,…,Yn примет совокупность значений, лежащих в пределах: (уi,уi+dуi), где i=1,2,…n. Так как опыты независимы, эта вероятность равна произведению элементов вероятностей (1) для всех значений i:
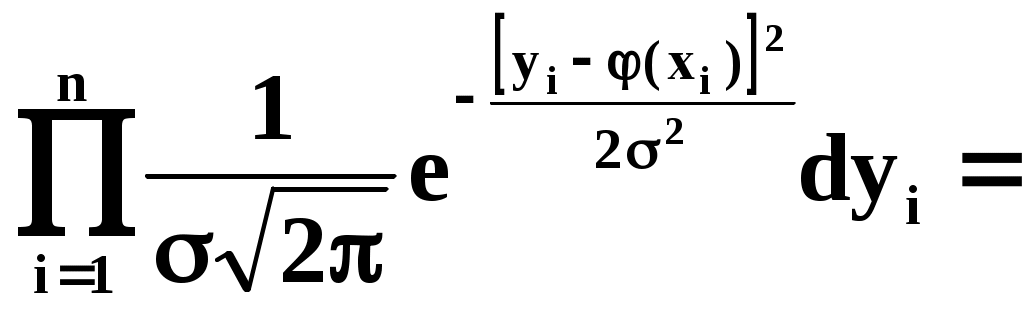
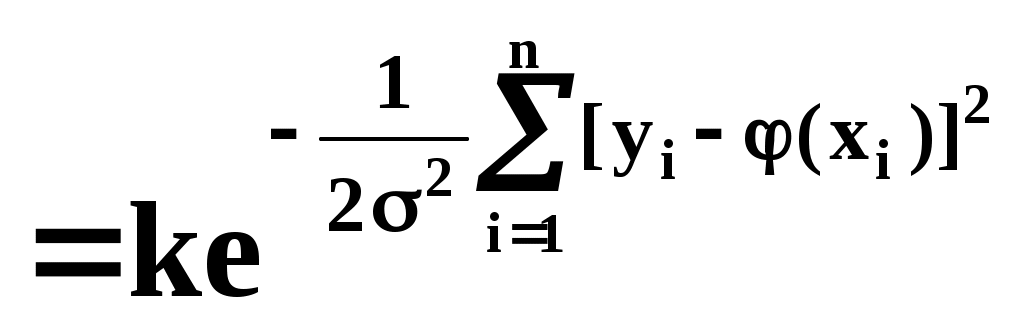 , (2)
, (2)
где k – коэффициент, не зависящий от (хi). Требуется так выбрать мат. ожидания (х1),(х2),…, (хn), чтобы (2) обращалась в максимум. Величина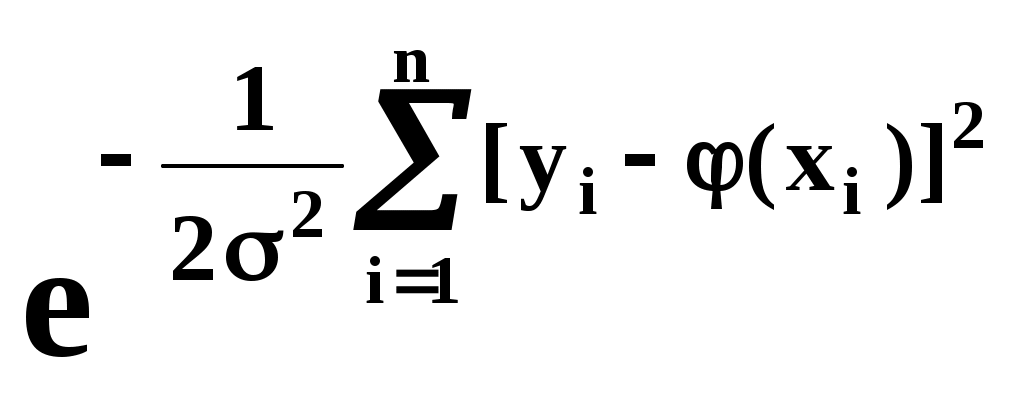 – всегда меньше 1. Очевидно, она имеет наибольшее значение, когда показатель степени (по абсолютной величине) минимален:
– всегда меньше 1. Очевидно, она имеет наибольшее значение, когда показатель степени (по абсолютной величине) минимален:
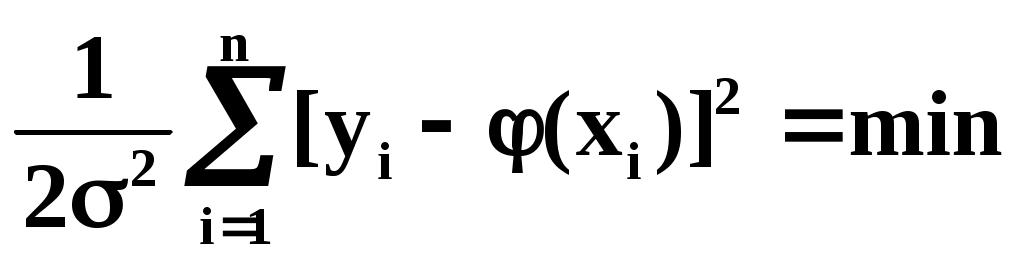
Отсюда, отбрасывая постоянный множитель 1/(2), получаем требование метода наименьших квадратов: Для того, чтобы данная совокупность наблюдённых значений у1,у2,…,уn была наивероятнейшей, нужно выбрать функцию
(х) так, чтобы сумма квадратов отклонений наблюдённых значений уi от (хi) была минимальной:
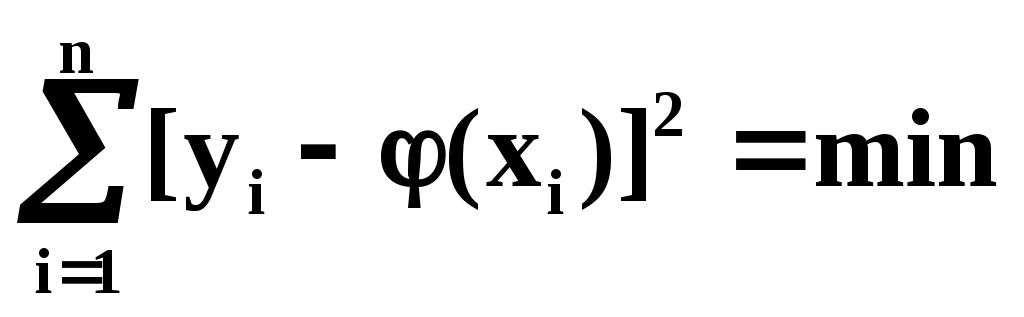
Таким образом обосновывается МНК, исходя из нормального закона ошибок измерения и требования максимальной вероятности данной совокупности ошибок. Перейдём к задаче определения параметров a,b,c,… Функция у=(х) содержит параметры a,b,c,…, т.е. можно записать: у=(x,a,b,c,…). Требуется выбрать a,b,c,… исходя из условия:
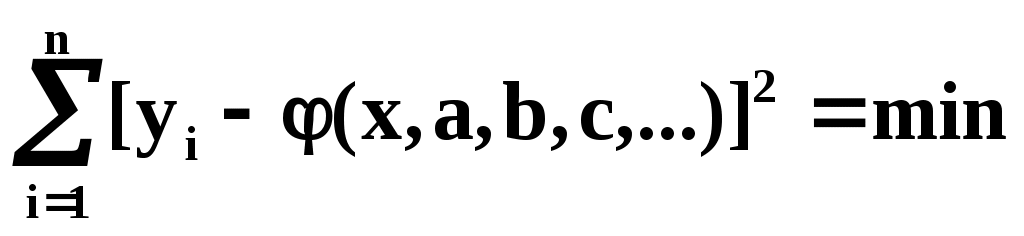 (3)
(3)
Найдём значения a,b,c,…, обращающие левую часть (3) в минимум. Для этого продифференцируем её по a,b,c,… и приравняем произведение нулю:
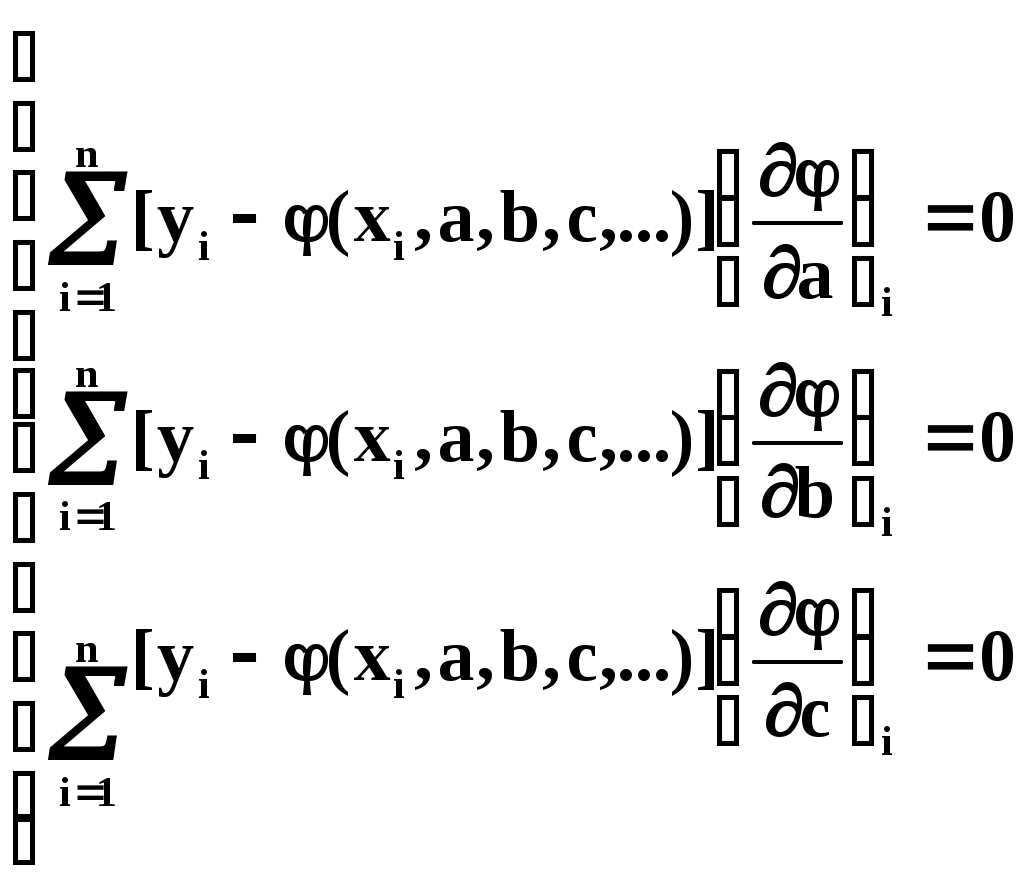
где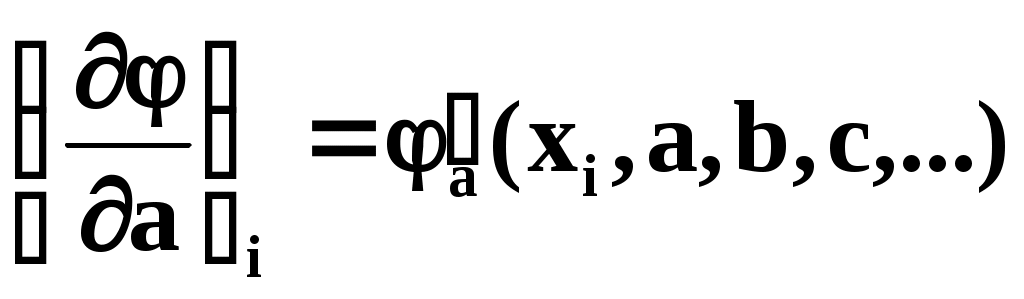 – значение частной производной функции по параметру а в точке xi.
– значение частной производной функции по параметру а в точке xi. 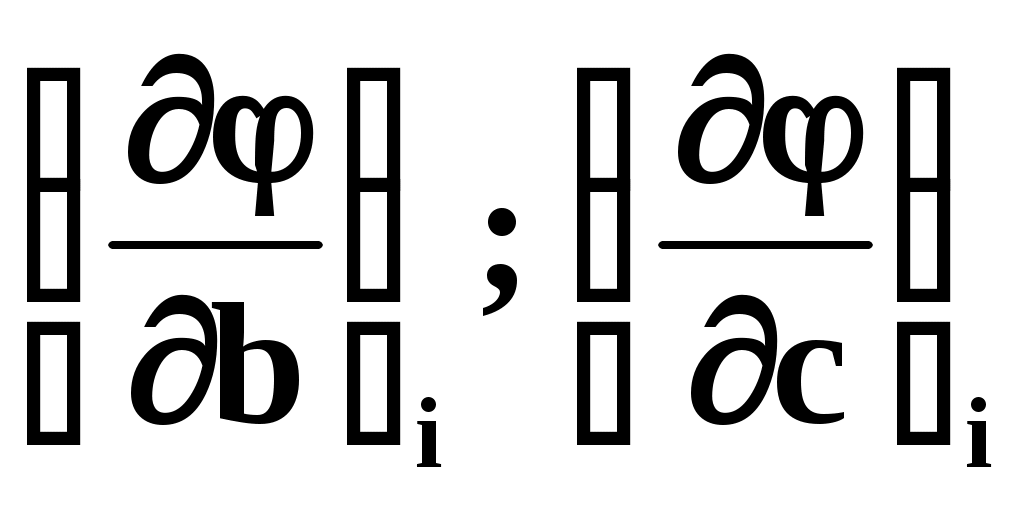 – аналогично. Система содержит столько же уравнений, сколько параметров a,b,c,… Решить эту систему в общем виде нельзя, необходимо задаться конкретным видом функции .
– аналогично. Система содержит столько же уравнений, сколько параметров a,b,c,… Решить эту систему в общем виде нельзя, необходимо задаться конкретным видом функции .
Рассмотрим два случая, наиболее часто встречающихся на практике:
1) когда – линейна; 2) когда – выражается полиномом второй степени (т.е.параболой).
Рассмотрим первый случай.
Подбор параметров линейной
функции методом МНК
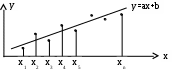
Требуется подобрать по МНК коэффициенты a и b линейной функции y=ax+b. Дифференцируем по a и b:
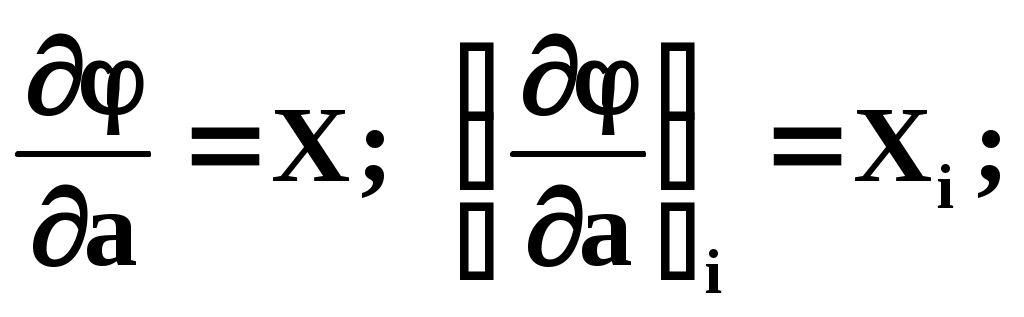
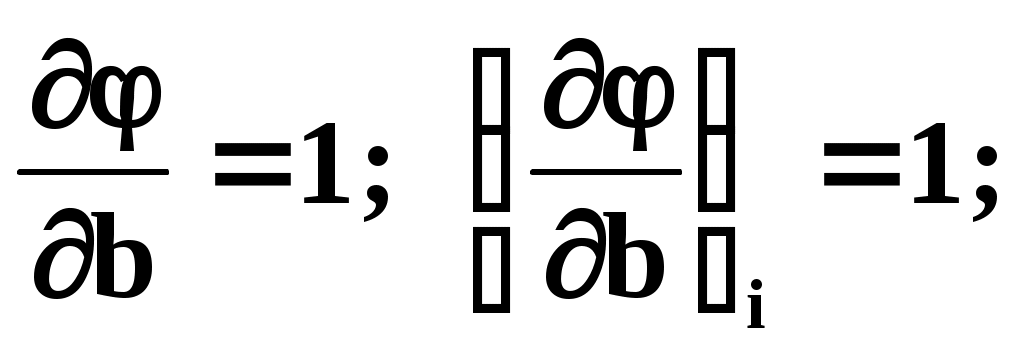
Подставляем производные в систему:
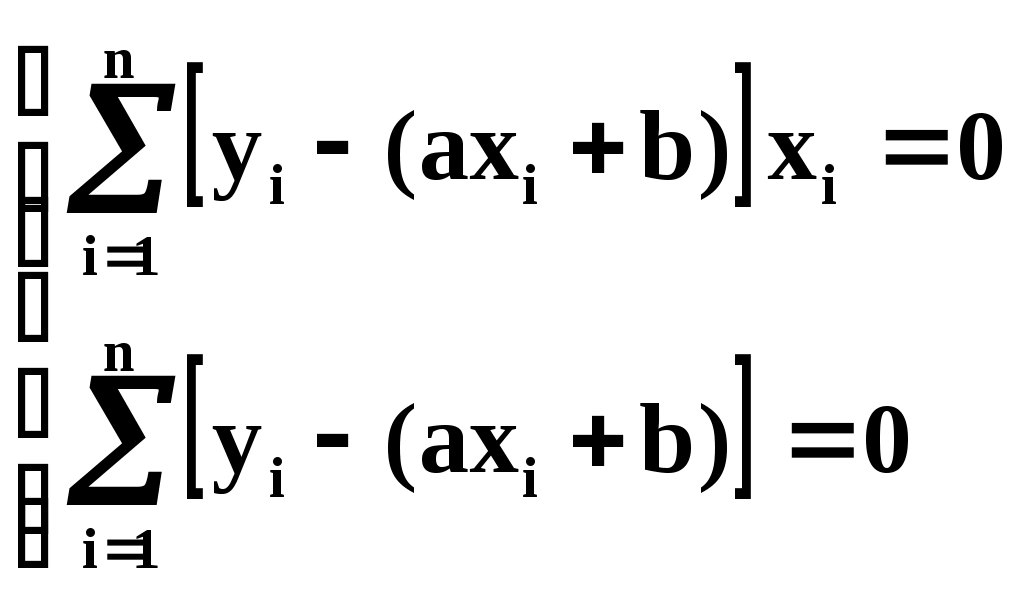
или раскрывая скобки и производя суммирование:
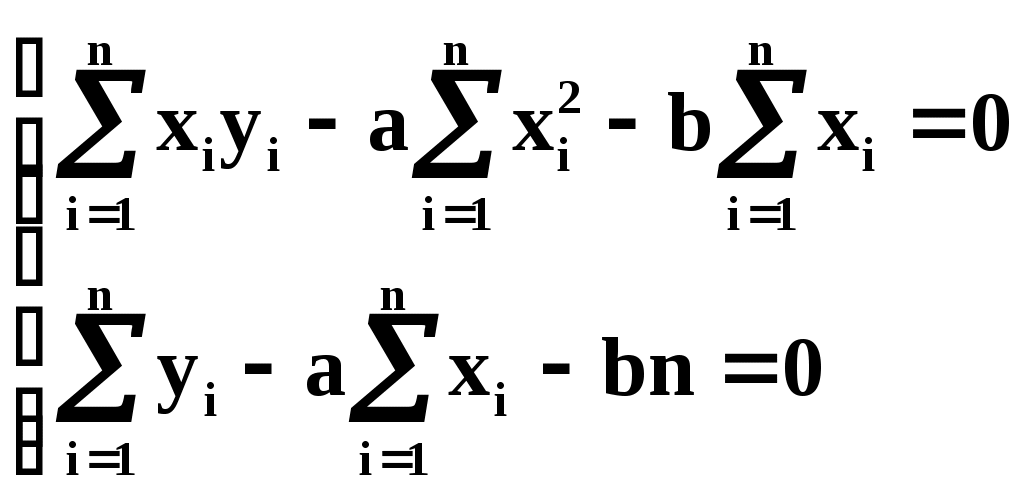
Разделим оба последних уравнения на n:
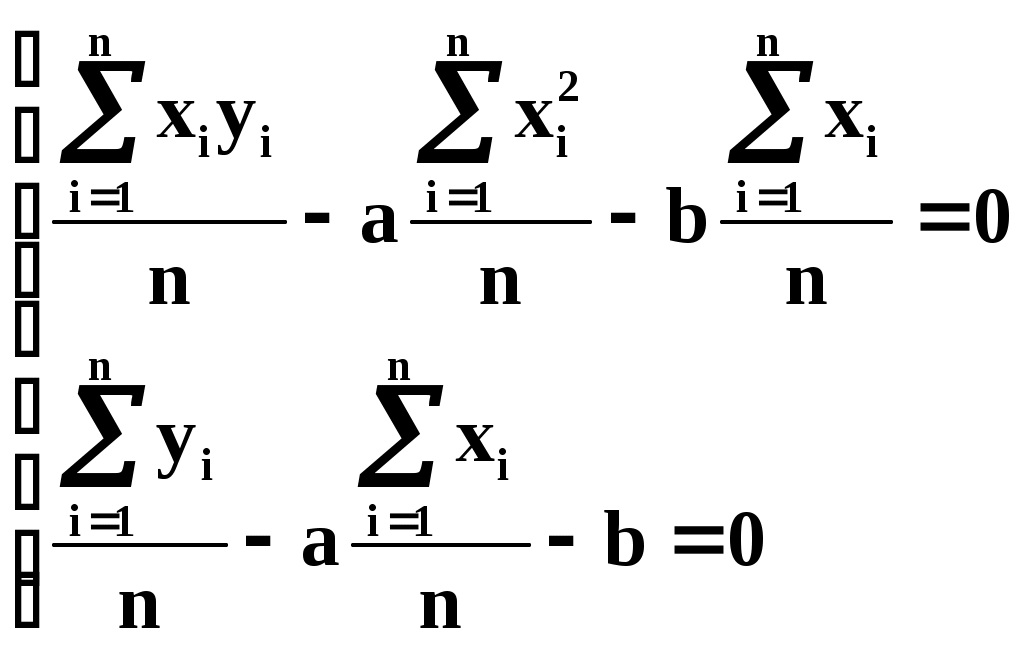
(4)
Суммы представляют собой статистические моменты. Обозначим их:
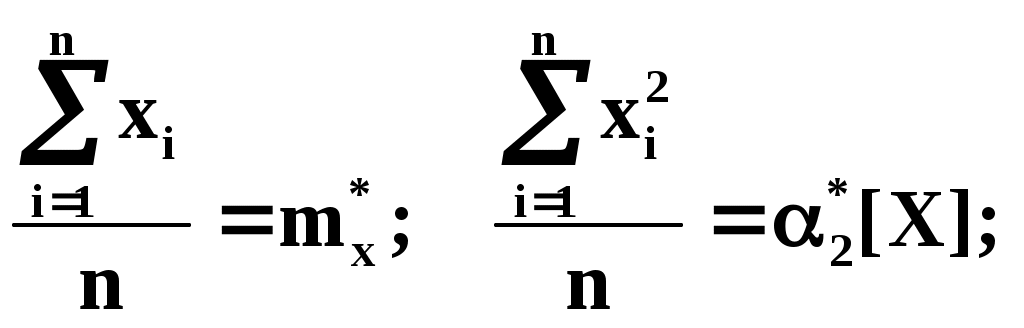
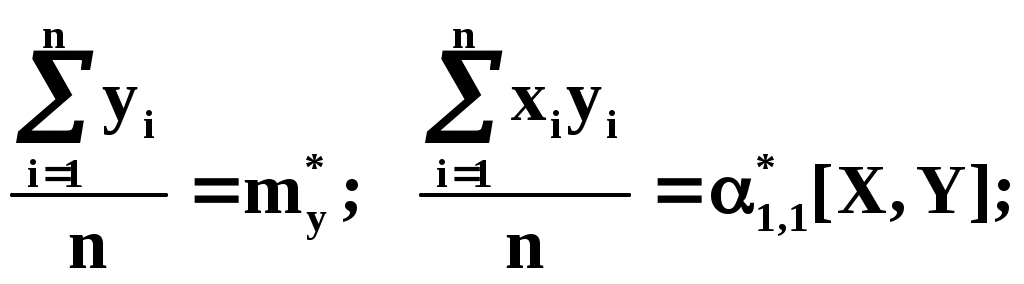
Подставляя в (4) эти выражения получаем:
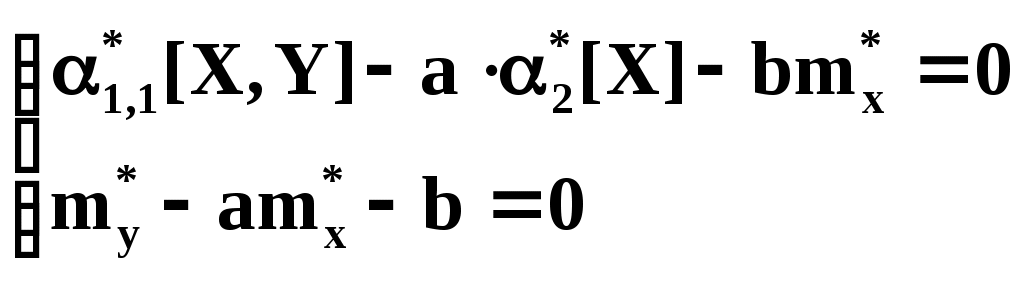
Выразим b из второго уравнения и подставим в первое:
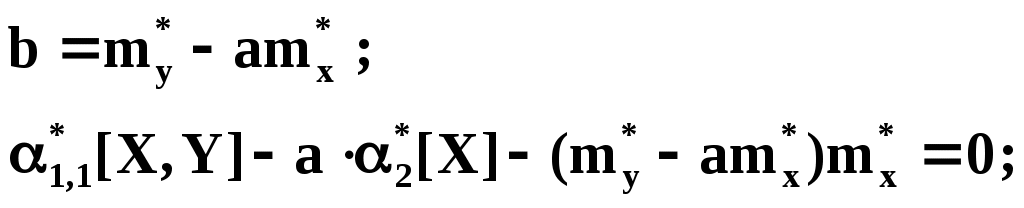
Решая последнее уравнение относительно а, имеем:
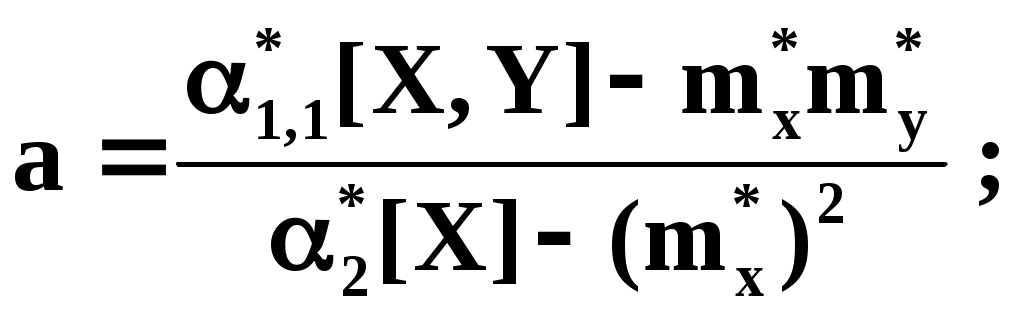
Упростим выражение, введя не начальные, а центральные моменты: (это доказано в книгах, неинтересно):
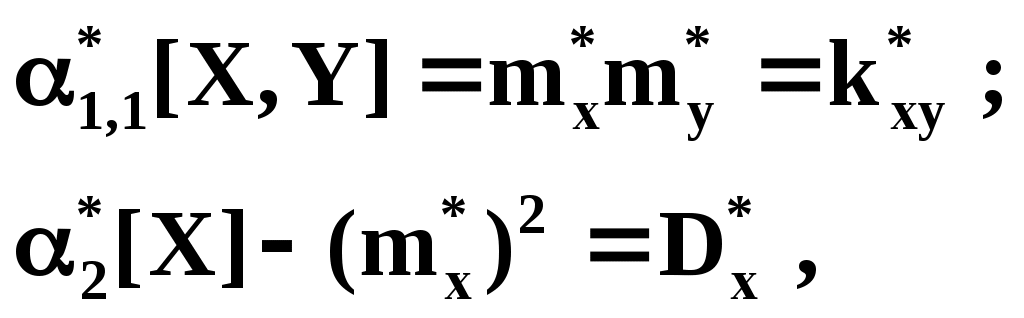
откуда:
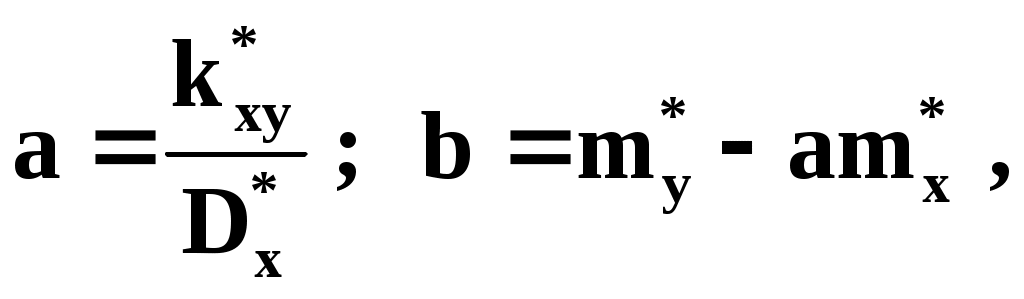
где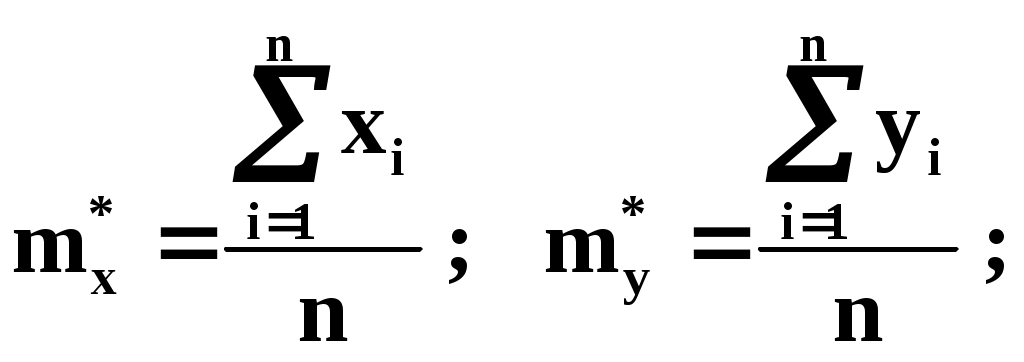
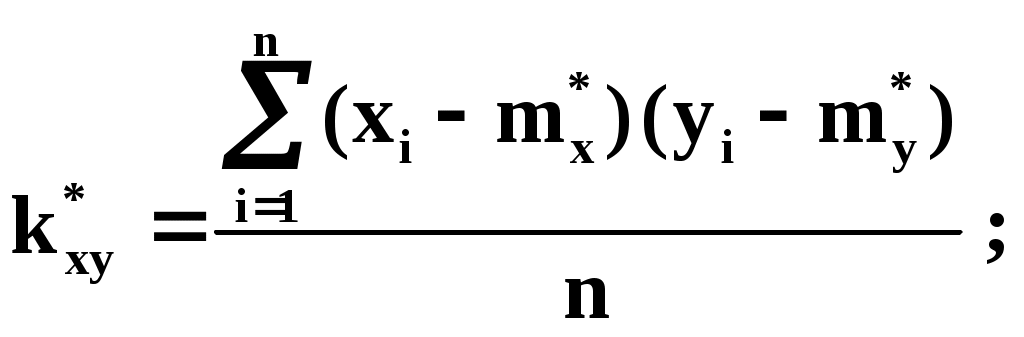
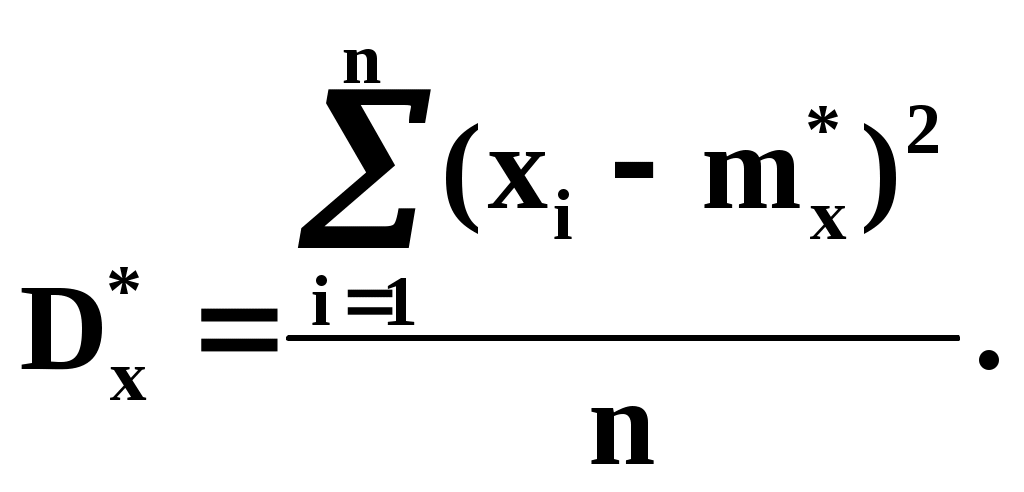
Докажем:
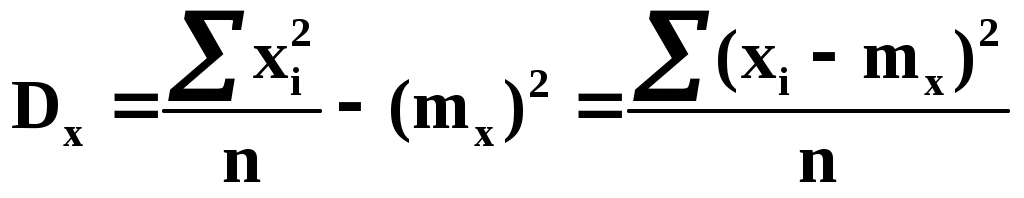
Раскроем правую часть
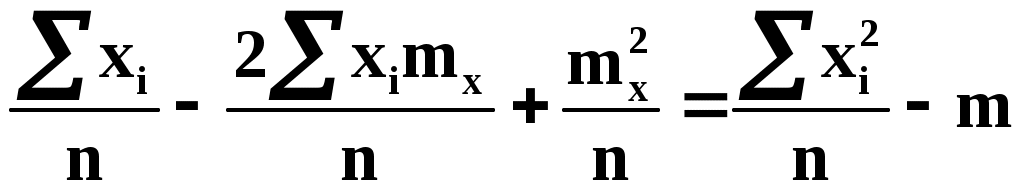
Таким образом, поставленная задача решена и линейная зависимость, связывающая х и у, имеет вид:
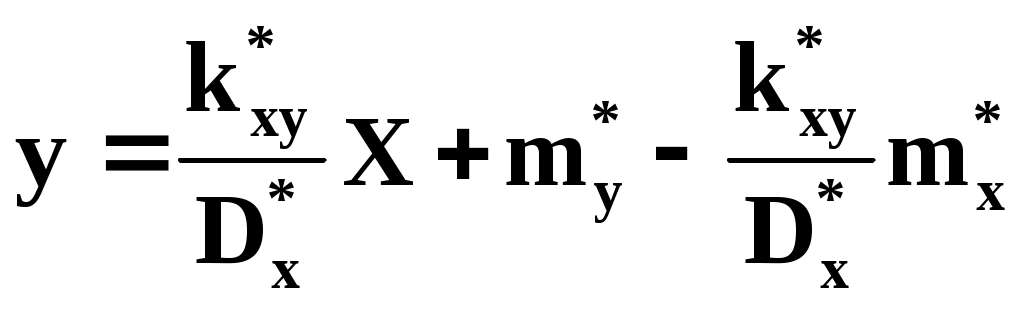
Рассмотрим второй случай.
Подбор параметров параболы
второго порядка методом МНК
Требуется подобрать по МНК параметры a,b,c квадратичной функции: Дифференцируем по a,b и c:
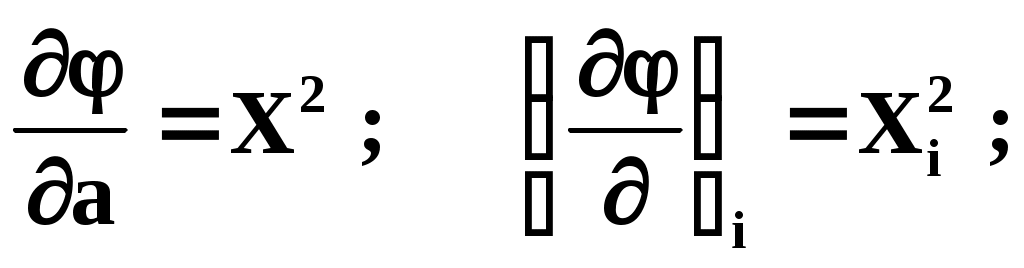
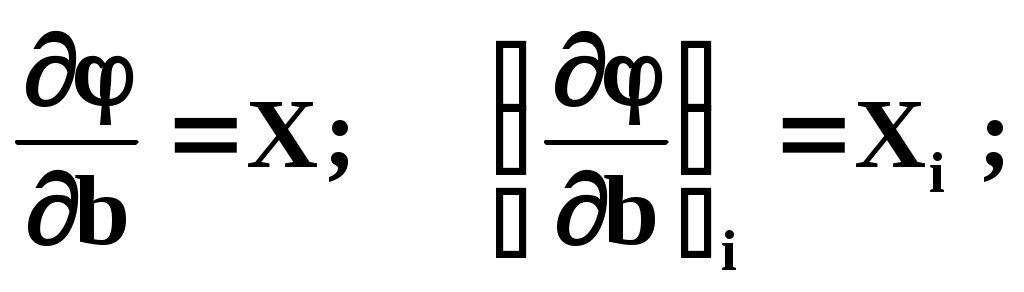
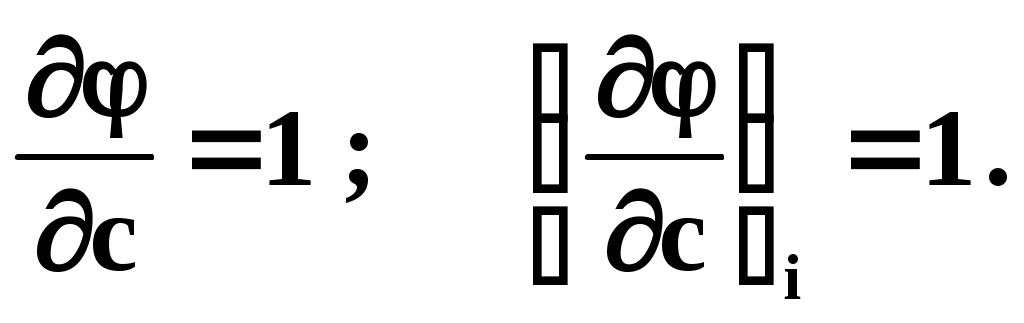
Подставляем производные в систему:
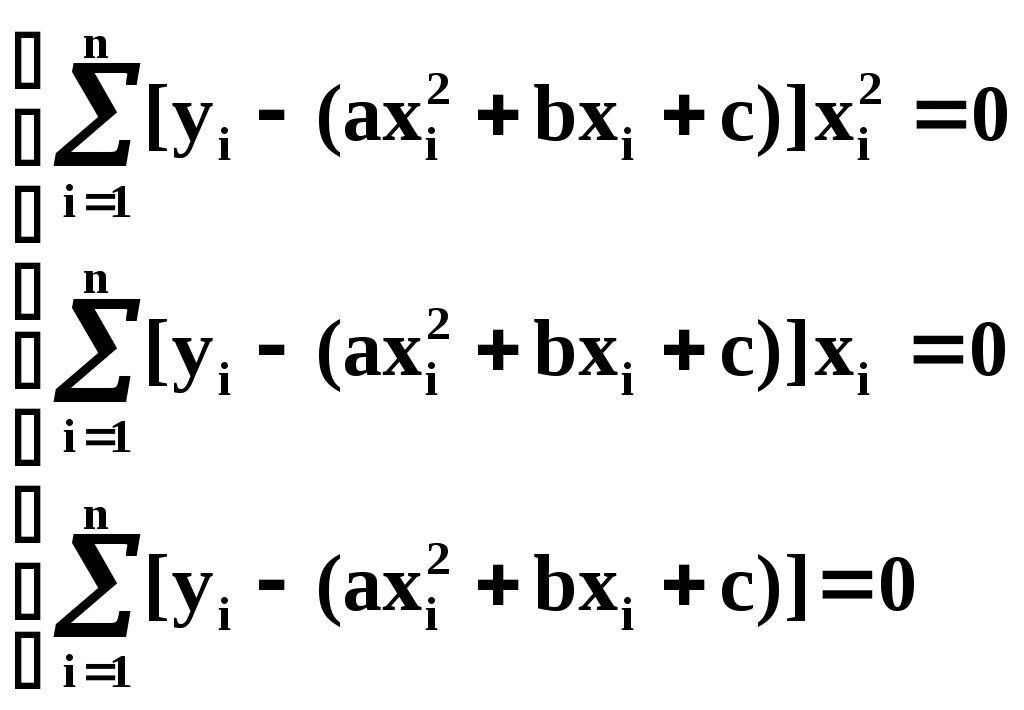
Или раскрывая скобки, приводя подобные члены и деля на n имеем (для простоты будем
использовать распространённое в литературе по МНК обозначение вместо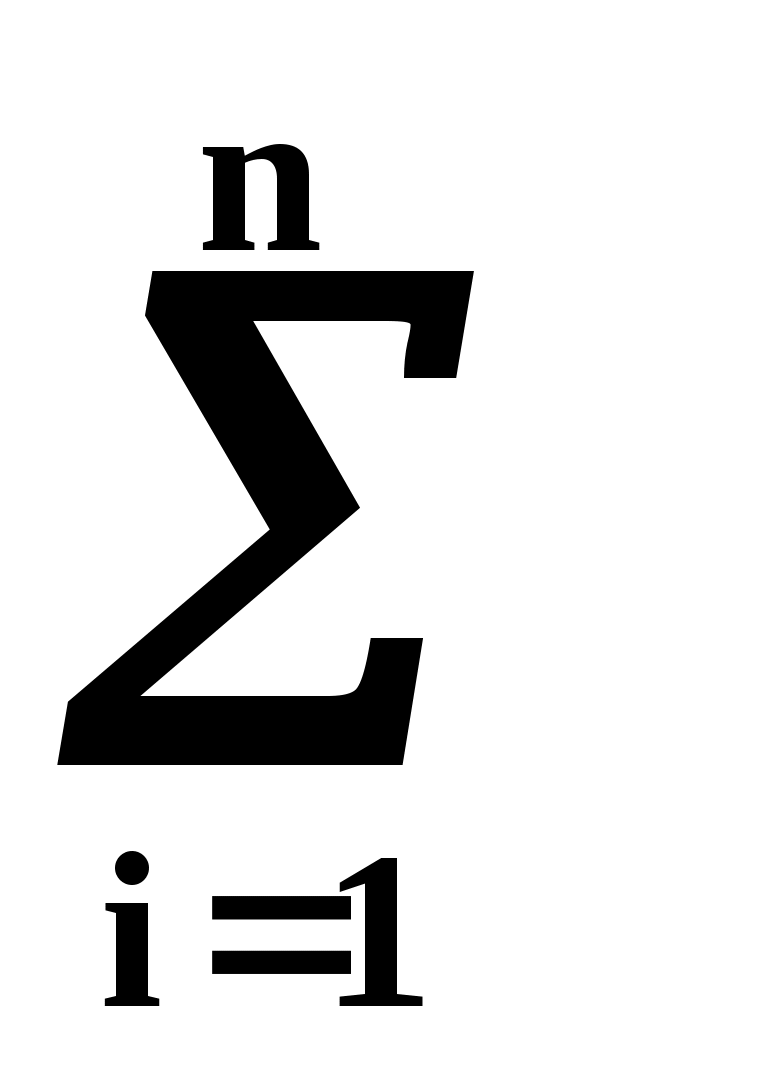 ):
):
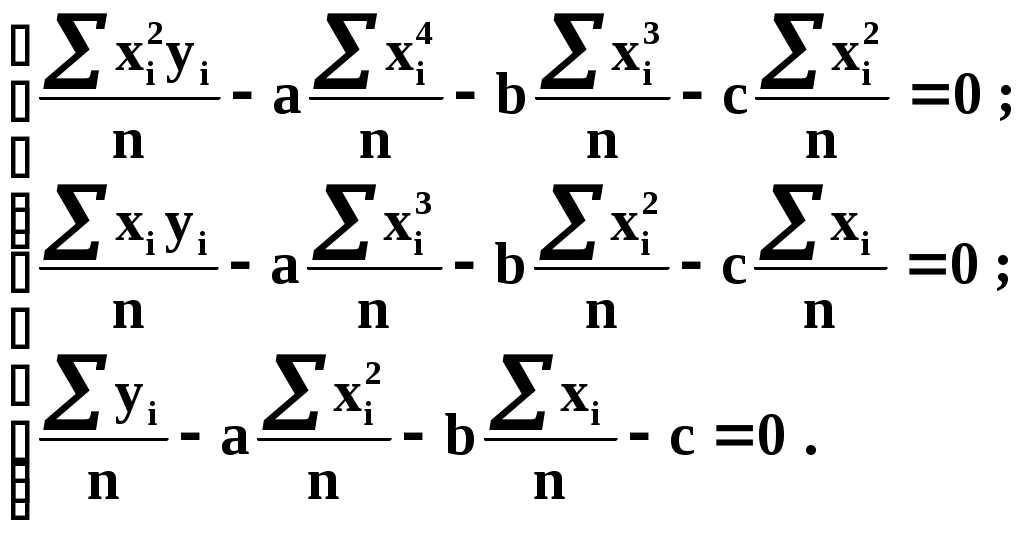
Коэффициенты этой системы также представляют собой статистические моменты двух величин X и Y:
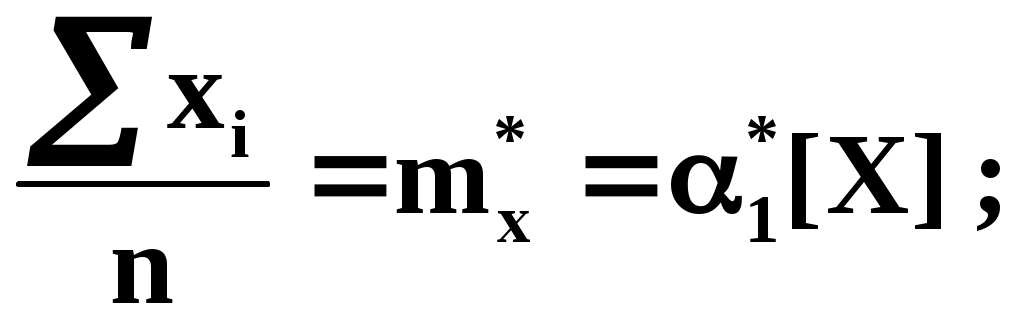
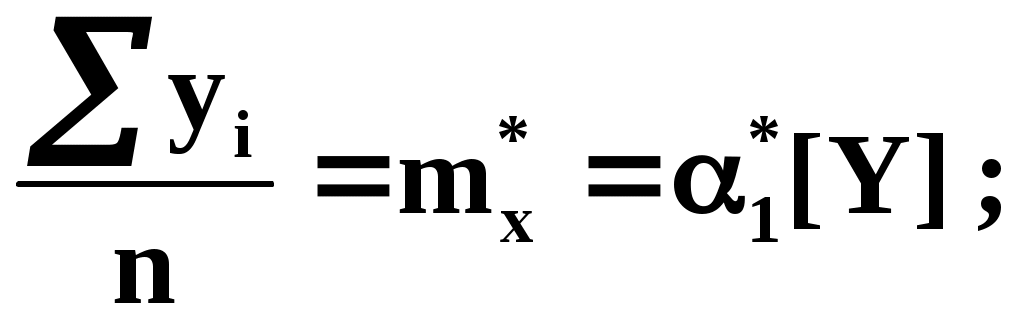
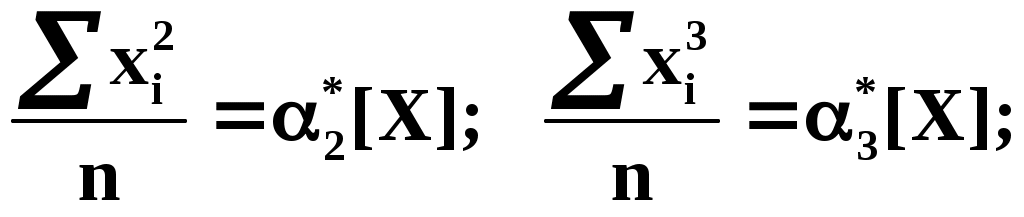
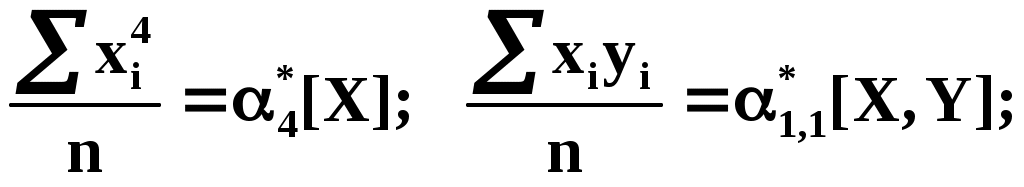
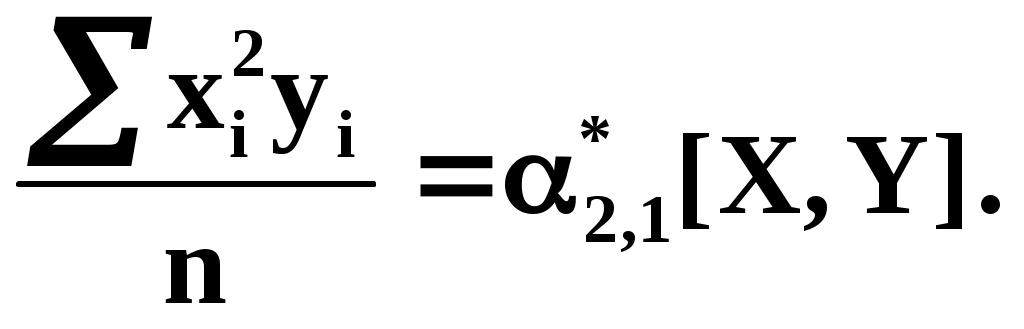
С помощью этих начальных моментов можно придать системе более компактный вид. Учитывая, что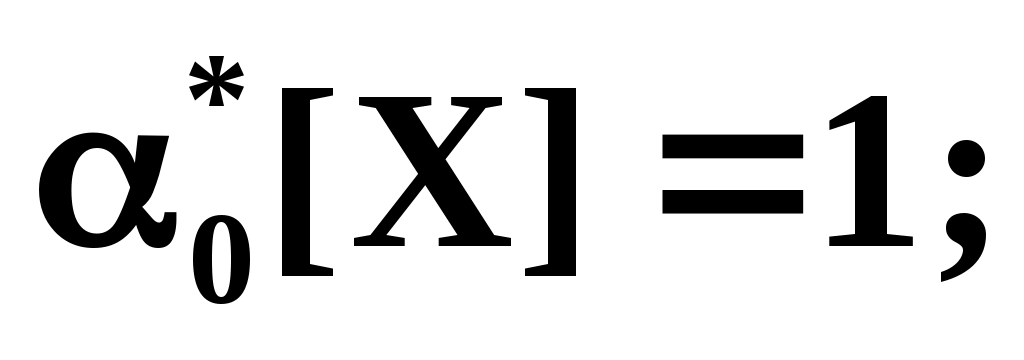
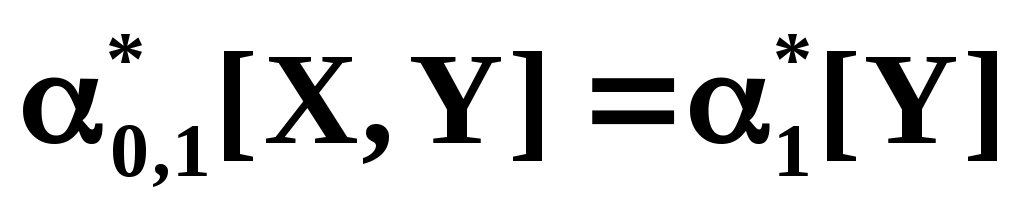 , запишем:
, запишем:
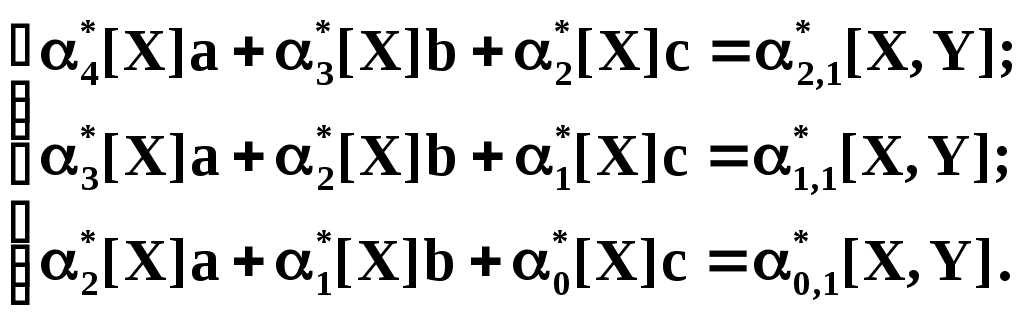
Решение этой системы даёт значения a,b,c для искомой функции. Но в общем виде это решение громоздко. Аналогичными по структуре будут уравнения для полинома любого порядка.
Полиномы, проходящие через заданные точки
На практике встречаются следующие задачи. Производится n измерений в каждой точке зависимости y=f(x). Затем в каждой точке находится среднее значение и средняя квадратическая погрешность. Далее решается задача подбора зависимости y=f(x), проходящей через все полученные точки.
Поскольку полиномы легко интегрируются и дифференцируются, такие многочленные модели находят широкое применение при небольшом числе экспериментальных точек. Так через данные две точки (х1,у1) и (х2,у2) можно провести только одну линию у=а0+а1х. Параметры этой прямой а0 и а1 определяются системой уравнений:
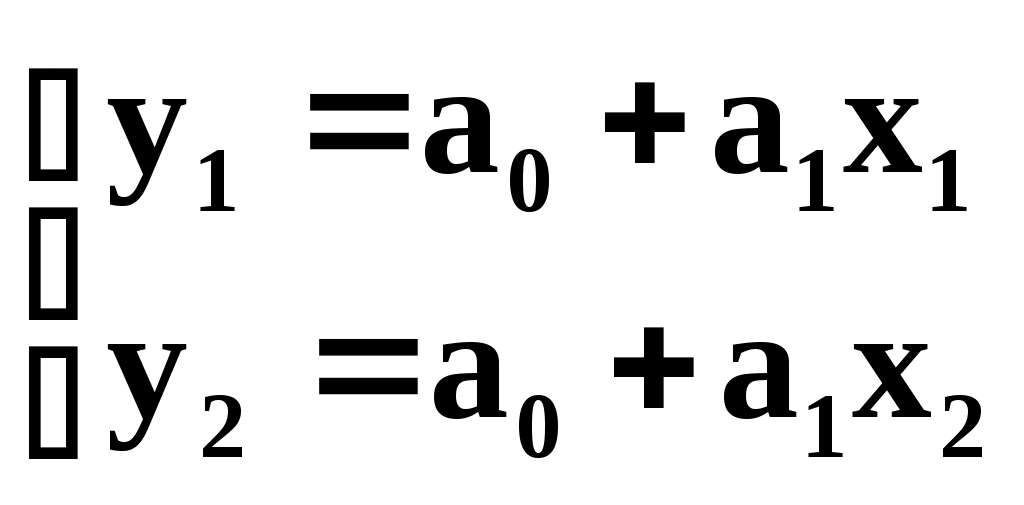
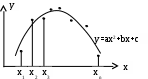
Подобным образом, через три различные точки можно провести только одну кривую не более чем второго порядка: у=а0+а1х+а2х2. Параметры а0,а1,а2 этой кривой определяются системой уравнений:
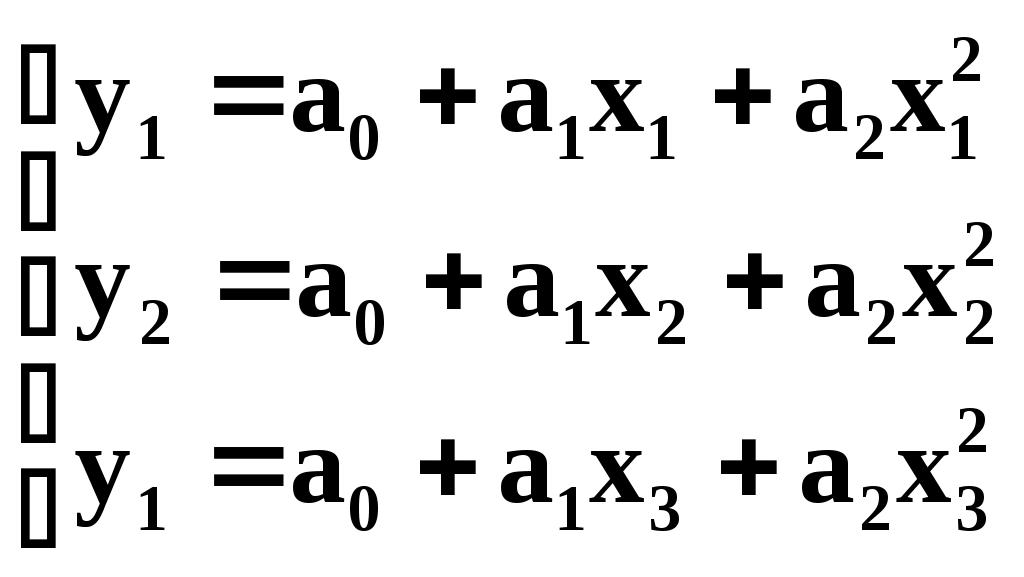
Для восьми экспериментальных точек в качестве эмпирической модели используется полином седьмой степени. Поскольку данный полином проходит через каждую из заданных точек, то результирующая сумма отклонений равна нулю.
Недостатками применения полиномов в построении эмпирических моделей являются:
1) чувствительность коэффициентов аi к малым изменениям в исходных данных.
2) очень сильные колебания значений полинома на концах заданного интервала.
При большом количестве экспериментальных данных используют сглаживающий полином более низкого порядка, полученный, например, по МНК.
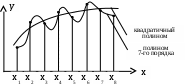
Для решения вопроса о порядке полинома для модели рассмотрим производные, например, полинома второго порядка у=а+bх+cх2;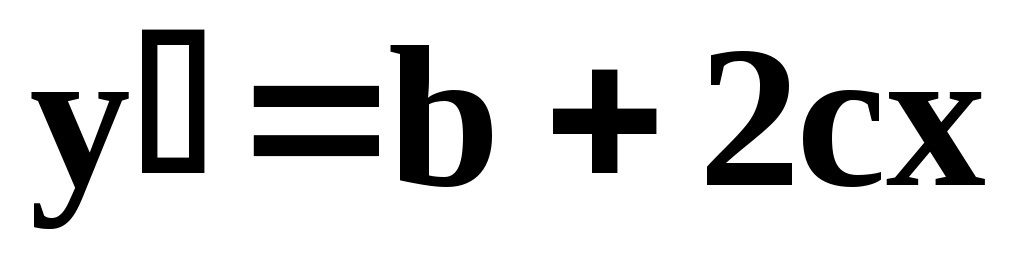 ;
; 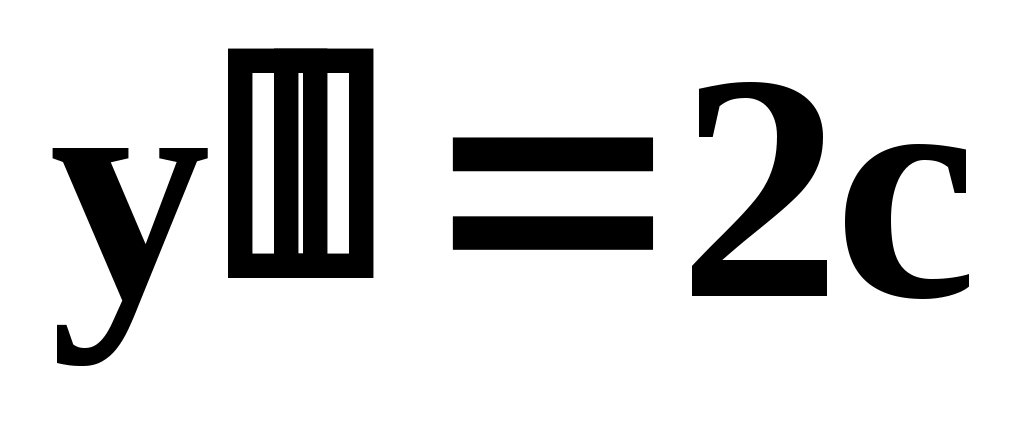
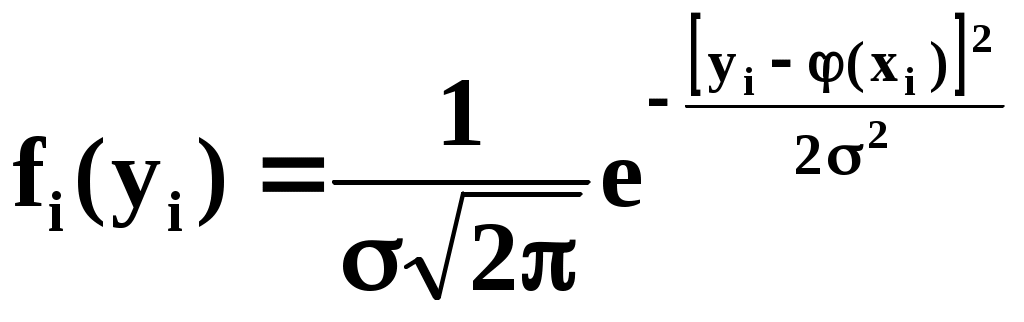
В результате нашего опыта (т.е. ряда измерений) произошло следующее событие: случайные величины (Y1,Y2,…,Yn) приняли совокупность значений (у1,у2,…,уn). Поставим задачу: так подобрать мат. ожидания (х1),(х2),…, (хn) чтобы вероятность этого события была максимальна (т.е. принцип максимального правдоподобия). Так как величины Yi непрерывны, то вероятность Yi=уi равна нулю. Поэтому будем пользоваться не вероятностями событий Yi=уi, а соответствующими элементами вероятностей:
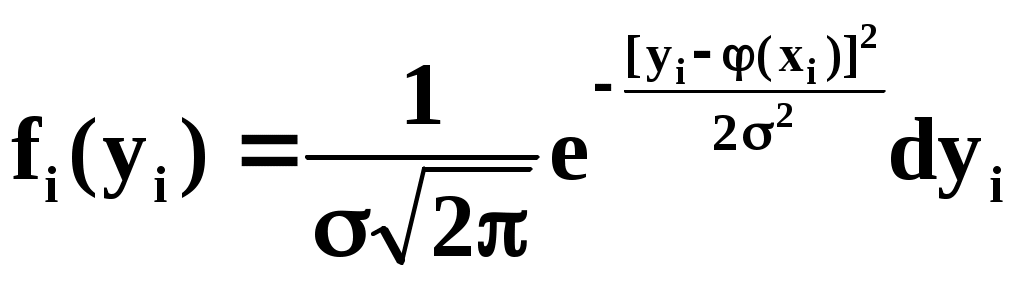 (1)
(1)Найдём вероятность того, что система случайных величин Y1,Y2,…,Yn примет совокупность значений, лежащих в пределах: (уi,уi+dуi), где i=1,2,…n. Так как опыты независимы, эта вероятность равна произведению элементов вероятностей (1) для всех значений i:
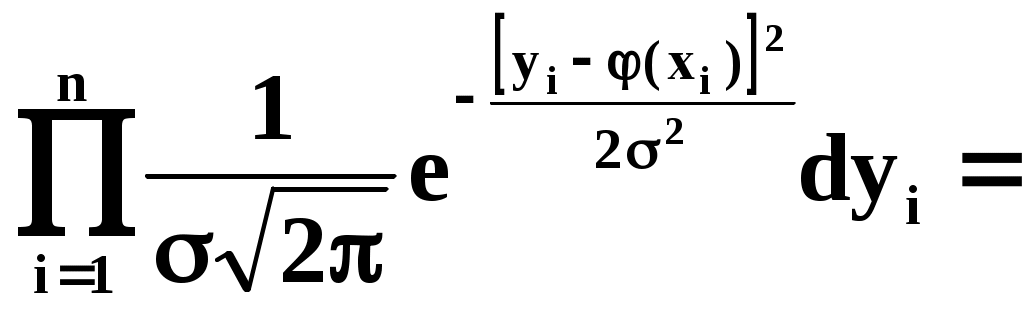
где k – коэффициент, не зависящий от (хi). Требуется так выбрать мат. ожидания (х1),(х2),…, (хn), чтобы (2) обращалась в максимум. Величина
Отсюда, отбрасывая постоянный множитель 1/(2), получаем требование метода наименьших квадратов: Для того, чтобы данная совокупность наблюдённых значений у1,у2,…,уn была наивероятнейшей, нужно выбрать функцию
(х) так, чтобы сумма квадратов отклонений наблюдённых значений уi от (хi) была минимальной:
Таким образом обосновывается МНК, исходя из нормального закона ошибок измерения и требования максимальной вероятности данной совокупности ошибок. Перейдём к задаче определения параметров a,b,c,… Функция у=(х) содержит параметры a,b,c,…, т.е. можно записать: у=(x,a,b,c,…). Требуется выбрать a,b,c,… исходя из условия:
Найдём значения a,b,c,…, обращающие левую часть (3) в минимум. Для этого продифференцируем её по a,b,c,… и приравняем произведение нулю:
где
Рассмотрим два случая, наиболее часто встречающихся на практике:
1) когда – линейна; 2) когда – выражается полиномом второй степени (т.е.параболой).
Рассмотрим первый случай.
Подбор параметров линейной
функции методом МНК

Требуется подобрать по МНК коэффициенты a и b линейной функции y=ax+b. Дифференцируем по a и b:
Подставляем производные в систему:
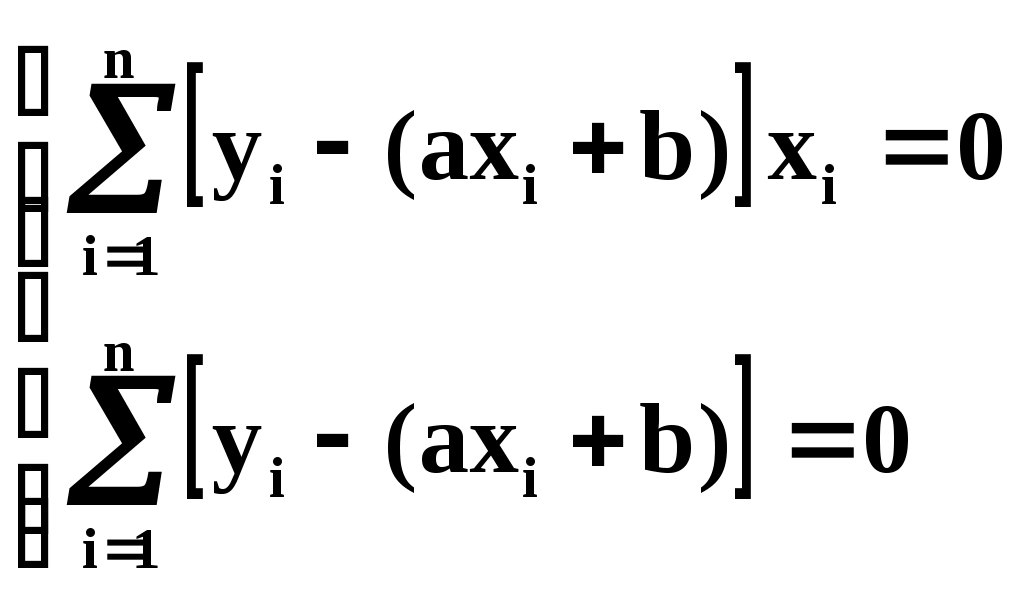
или раскрывая скобки и производя суммирование:
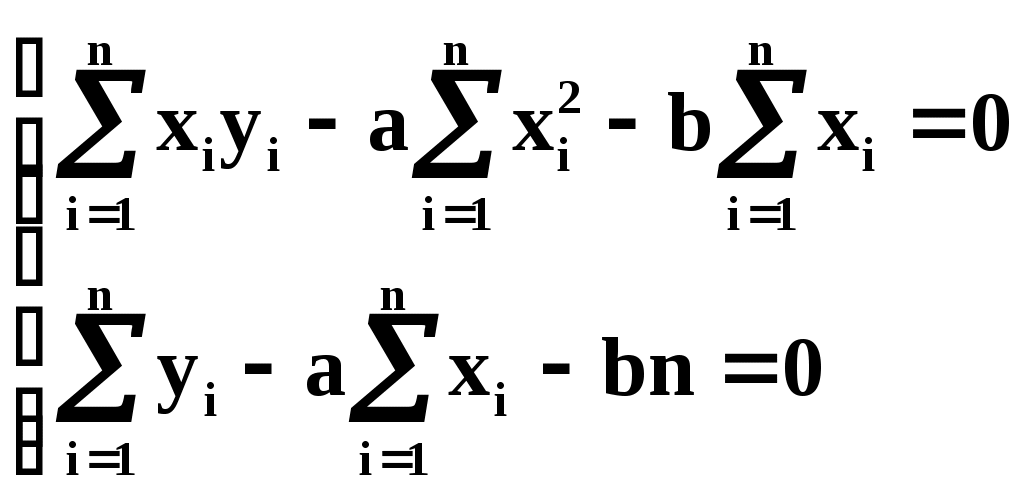
Разделим оба последних уравнения на n:
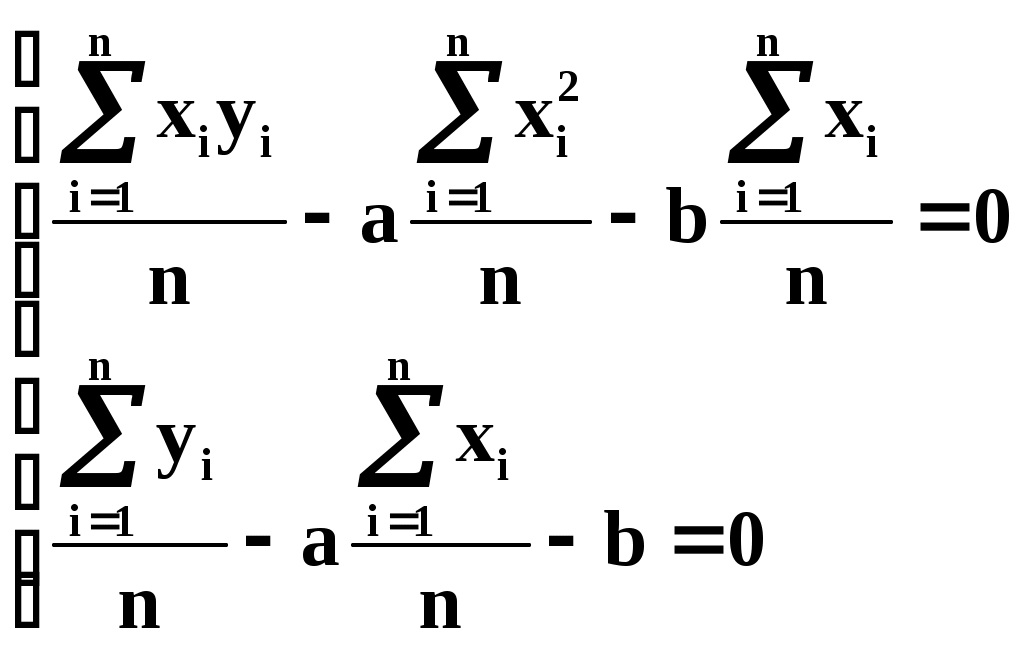
(4)
Суммы представляют собой статистические моменты. Обозначим их:
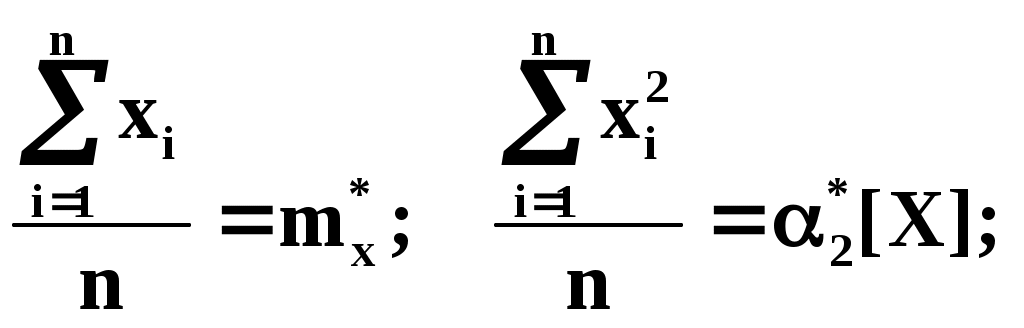
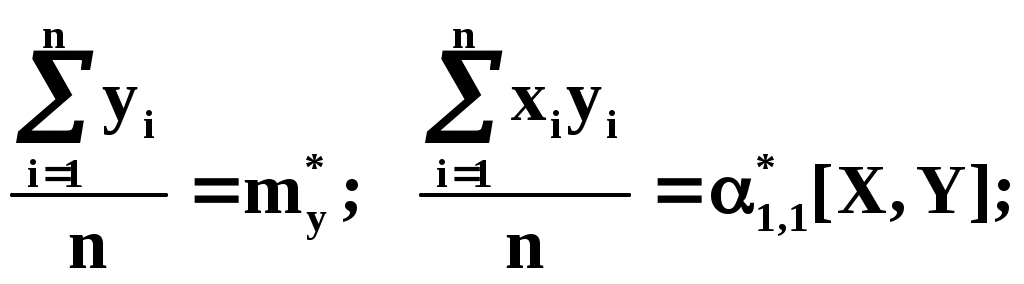
Подставляя в (4) эти выражения получаем:
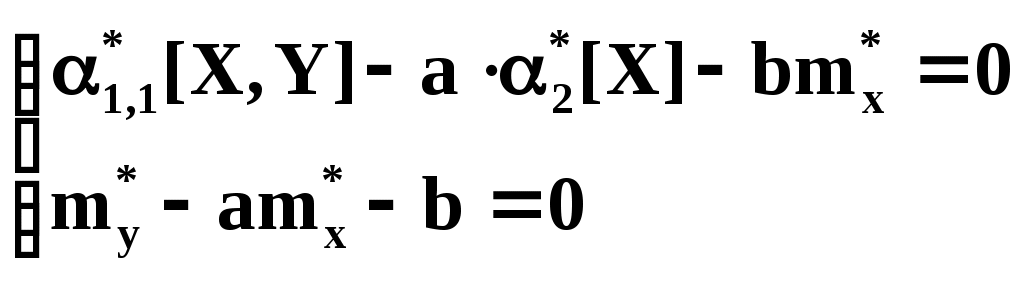
Выразим b из второго уравнения и подставим в первое:
Решая последнее уравнение относительно а, имеем:
Упростим выражение, введя не начальные, а центральные моменты: (это доказано в книгах, неинтересно):
откуда:
где
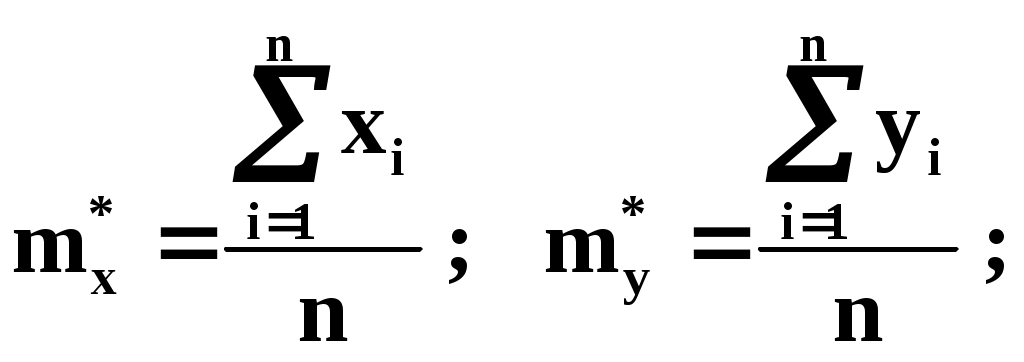
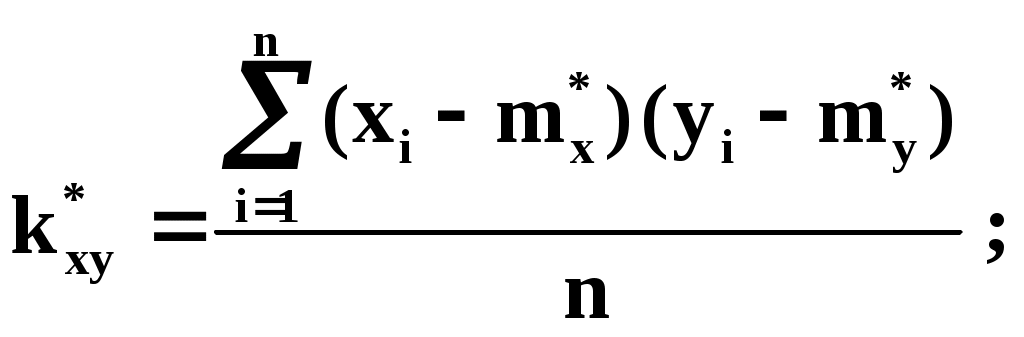
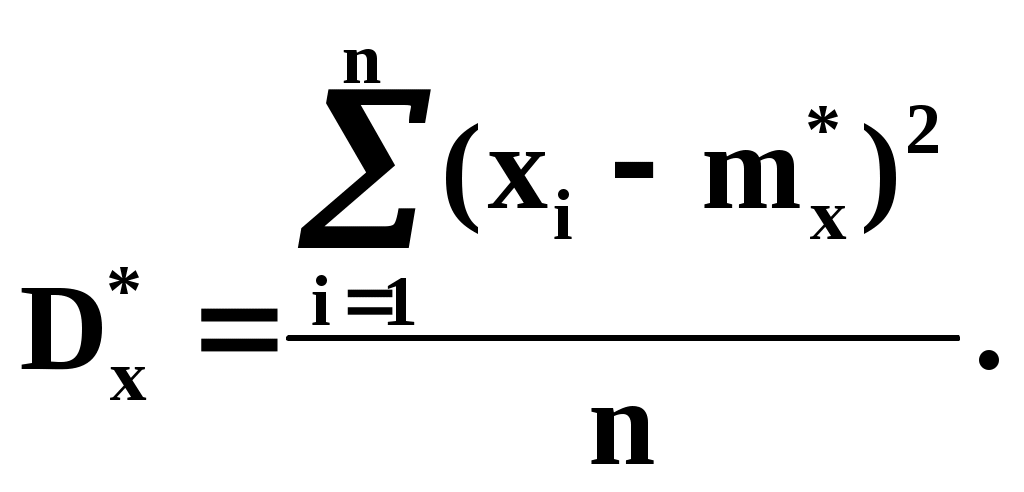
Докажем:
Раскроем правую часть
Таким образом, поставленная задача решена и линейная зависимость, связывающая х и у, имеет вид:
Рассмотрим второй случай.
Подбор параметров параболы
второго порядка методом МНК

Требуется подобрать по МНК параметры a,b,c квадратичной функции: Дифференцируем по a,b и c:
Подставляем производные в систему:
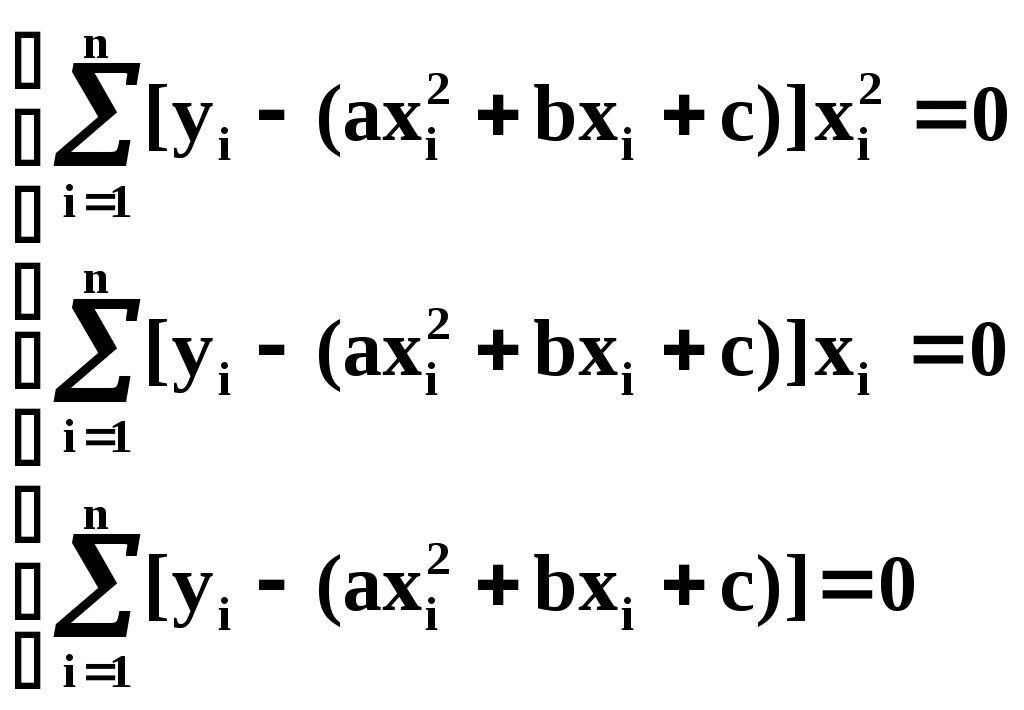
Или раскрывая скобки, приводя подобные члены и деля на n имеем (для простоты будем
использовать распространённое в литературе по МНК обозначение вместо
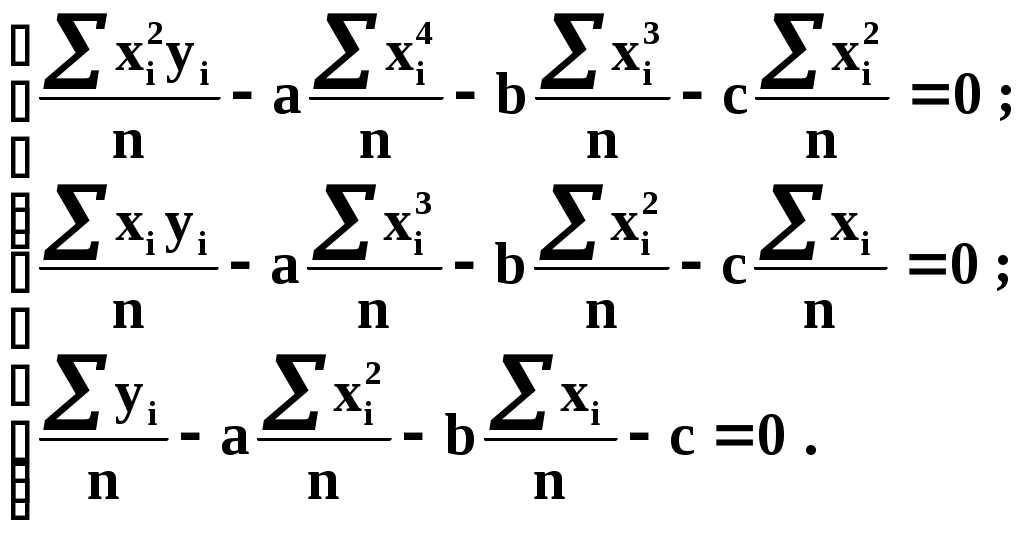
Коэффициенты этой системы также представляют собой статистические моменты двух величин X и Y:
С помощью этих начальных моментов можно придать системе более компактный вид. Учитывая, что
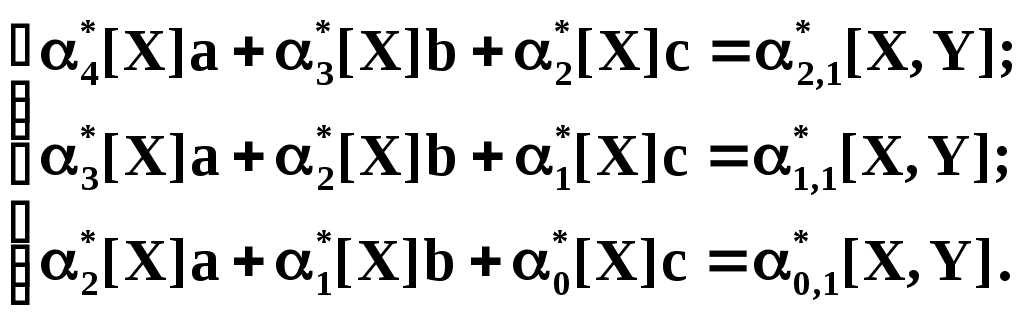
Решение этой системы даёт значения a,b,c для искомой функции. Но в общем виде это решение громоздко. Аналогичными по структуре будут уравнения для полинома любого порядка.
Полиномы, проходящие через заданные точки
На практике встречаются следующие задачи. Производится n измерений в каждой точке зависимости y=f(x). Затем в каждой точке находится среднее значение и средняя квадратическая погрешность. Далее решается задача подбора зависимости y=f(x), проходящей через все полученные точки.
Поскольку полиномы легко интегрируются и дифференцируются, такие многочленные модели находят широкое применение при небольшом числе экспериментальных точек. Так через данные две точки (х1,у1) и (х2,у2) можно провести только одну линию у=а0+а1х. Параметры этой прямой а0 и а1 определяются системой уравнений:
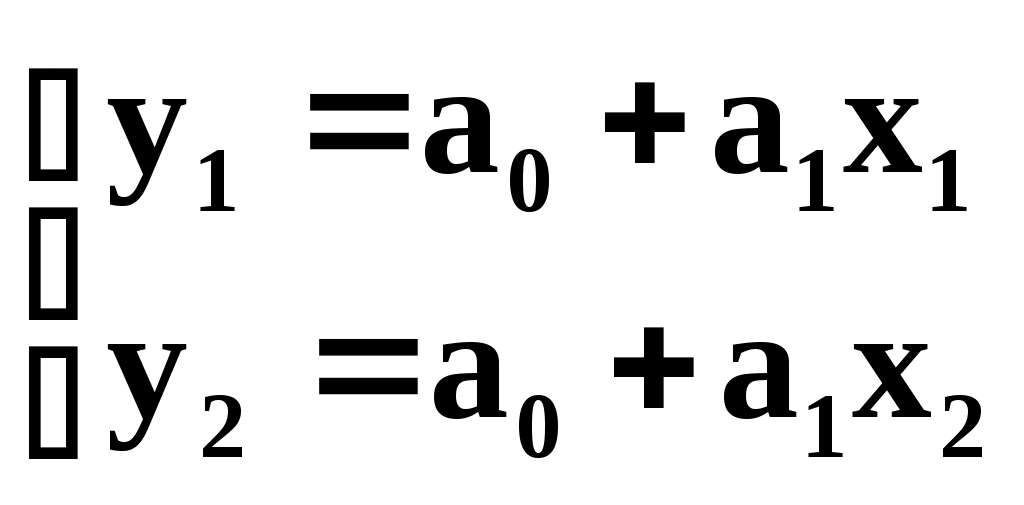
Подобным образом, через три различные точки можно провести только одну кривую не более чем второго порядка: у=а0+а1х+а2х2. Параметры а0,а1,а2 этой кривой определяются системой уравнений:
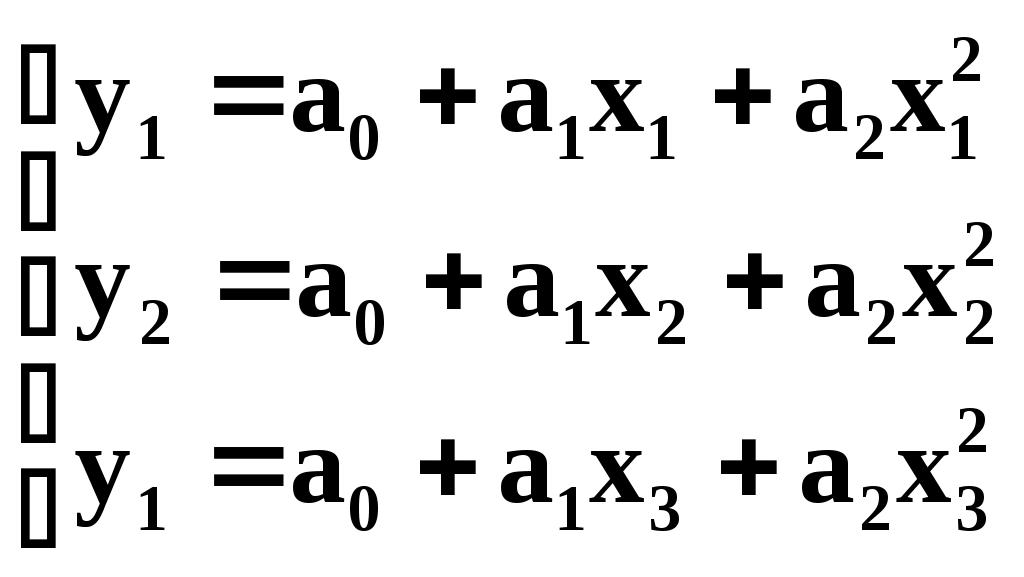
Для восьми экспериментальных точек в качестве эмпирической модели используется полином седьмой степени. Поскольку данный полином проходит через каждую из заданных точек, то результирующая сумма отклонений равна нулю.
Недостатками применения полиномов в построении эмпирических моделей являются:
1) чувствительность коэффициентов аi к малым изменениям в исходных данных.
2) очень сильные колебания значений полинома на концах заданного интервала.
При большом количестве экспериментальных данных используют сглаживающий полином более низкого порядка, полученный, например, по МНК.
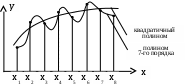
Для решения вопроса о порядке полинома для модели рассмотрим производные, например, полинома второго порядка у=а+bх+cх2;


