ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

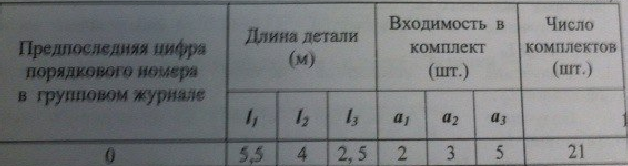

Запишем все варианты раскроя:
| Длина заготовок, м | Вариант раскроя | Возможное число деталей | Отход, м | Число заготовок, раскраиваемых по данному варианту | ||||
| длиной l1, м | длиной l2, м | длиной l3, м | ||||||
| L1 | 1 2 3 4 5 6 | 2 1 0 0 0 0 | 0 1 3 2 1 0 | 0 1 0 1 3 4 | 1 0 0 1,5 0,5 2 | x1 x2 x3 x4 x5 x6 | ||
| L2 | 1 2 3 4 5 6 7 8 9 | 2 2 1 1 1 0 0 0 0 | 1 0 2 1 0 3 2 1 0 | 0 1 0 2 3 1 2 4 6 | 0 1,5 1,5 0,5 2 0,5 2 1 0 | x7 x8 x9 x10 x11 x12 x13 x14 x15 | ||
| L3 | 1 2 3 4 | 1 0 0 0 | 0 2 1 0 | 1 0 2 3 | 1 1 0 1,5 | x16 x17 x18 x19 | ||
1. Составьте математическую модель получения максимального количества комплектов деталей из всех заготовок.
Для этого вводится еще одна переменная: x
20 – количество комплектов деталей. При этом математическая модель для случая трех видов заготовок и комплектов, состоящих из трех видов деталей, записывается следующим образом.
Целевая функция:
x0 =x20 (max) .
Система ограничений:
– по комплектности:
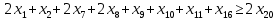

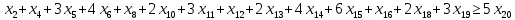
– по ресурсам заготовок:
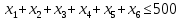

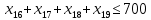
Условие неотрицательности и целочисленности переменных:

2. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L1.
Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом.
Целевая функция:
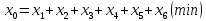
Система ограничений:
– по комплектности:
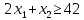
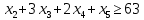
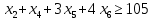
– по ресурсам заготовок длиной L1:
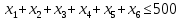
Условие неотрицательности и целочисленности переменных:
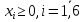
3. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L2.
Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом.
Целевая функция:
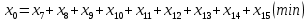
Система ограничений:
– по комплектности:
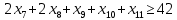
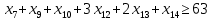
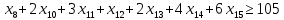
– по ресурсам заготовок длиной L2:

Условие неотрицательности и целочисленности переменных:
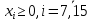
4. Составьте математическую модель получения Мкомплектов деталей из наименьшего числа заготовок длиной L3.
Математическая модель для случая использования только заготовок первого типа, а комплекты состоят из деталей 3 видов, записывается следующим образом.
Целевая функция:
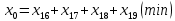
Система ограничений:
– по комплектности:
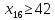
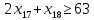
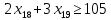
– по ресурсам заготовок длиной L2:

Условие неотрицательности и целочисленности переменных:

5. Составить математическую модель получения Мкомплектов деталей из всех заготовок данного типоразмера при минимальных отходах материала.
Математическая модель при использовании заготовок всех типов и Мкомплектов, состоящих из деталей трех видов, записывается следующим образом.
Целевая функция:
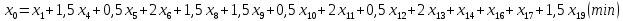
Система ограничений:
– по комплектности:
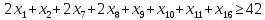
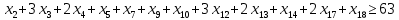
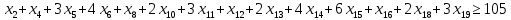
– по ресурсам заготовок:



Условие неотрицательности и целочисленности решений:
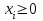 , x
, x
i – целое, где
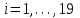 .
.

