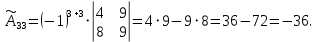
Таким образом, присоединенная матрица имеет вид:



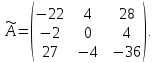
Вычислим обратную матрицу:



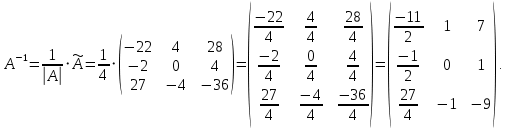
Теперь найдем матрицу :





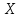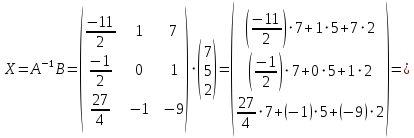
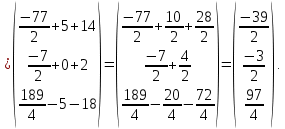
Получили:



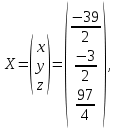
т. е. решение системы , , .

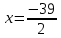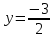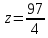2. Решим систему методом Крамера.

Так как 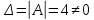, то по теореме Крамера система имеет единственное решение.

Вычислим определители матриц 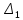, , 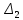, 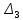полученных из матрицы 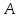заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

---

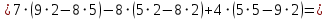
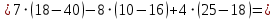
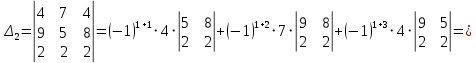
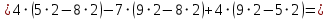
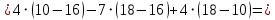
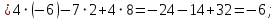
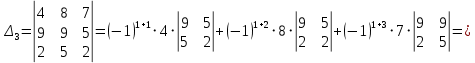
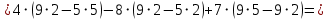
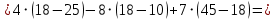
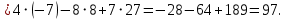
Теперь по формулам Крамера



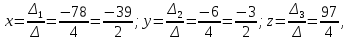
т. е. решение системы , , .

3. Решим систему методом Гаусса.

Расширенная матрица системы имеет вид:



Поменяем местами первую и последнюю строки:



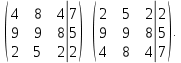
Разделим первую строку матрицы на :



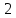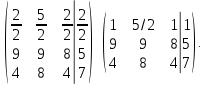
Так как 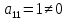, то умножая первую строку матрицы на числа 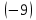, 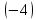и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную 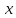из всех строк, начиная со второй: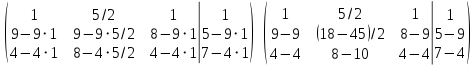





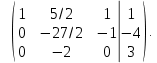
В результате преобразований нам также удалось избавиться от переменной 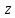в третьей строке, значит, в дальнейшем приведении матрицы к ступенчатому виду нет необходимости.

Получили систему уравнений:



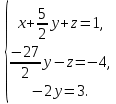
Отсюда, используя обратный ход метода Гаусса, найдем из третьего уравнения значение переменной :



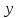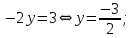
из второго – переменной :



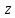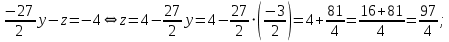
из первого – переменной :

---

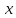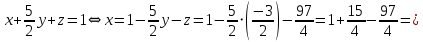
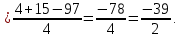
Таким образом, решение системы , , .

Ответ: ; ; .

Задание 3. Даны точки 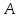, , 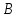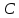на плоскости.

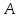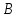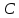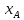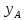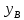7	6		1	4		4	1

a) Найдите уравнения прямой (параметрическое, каноническое, общее, с угловым коэффициентом, в отрезках).

b) Найдите длину отрезка .

c) Найдите уравнение прямой, перпендикулярной прямой и проходящей через точку C.

d) Найдите уравнение прямой, параллельной прямой и проходящей через точку .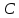

e) Найдите длину перпендикуляра, опущенного на прямую

---

из точки .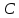

f) Найдите косинус угла .

g) Найдите площадь треугольника .

Постройте все найденные прямые, а также сам треугольник на одном чертеже.

Решение.

a) Составим каноническое уравнение прямой :



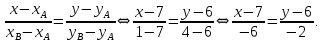
Упростим полученное уравнение, умножив обе части уравнения на :



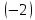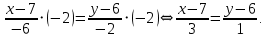
Приведём уравнение к параметрической форме:



От канонического уравнения перейдём к общему уравнению:



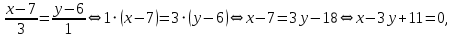
и уравнению с угловым коэффициентом:



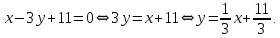
Наконец, получим уравнение прямой в отрезках: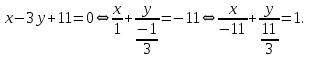



b) Вычислим длину отрезка :



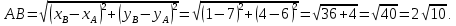
c) Уравнение высоты 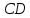будем искать в виде .

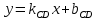Угловой коэффициент прямой 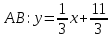равен 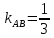. Высота 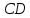перпендикулярна прямой , значит, ее угловой коэффициент 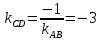. Значение параметра 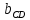найдем из условия, что прямая 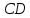проходит через точку

---

:



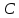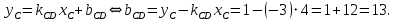
Таким образом, уравнение прямой 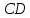имеет вид .

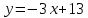d) Уравнение прямой 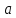, параллельной прямой , также будем искать в виде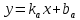
.

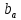Угловые коэффициенты у параллельных прямых равны, поэтому . Значение параметра найдем из условия, что прямая 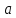проходит через точку :



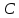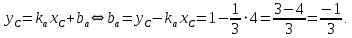
Таким образом, уравнение прямой 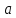имеет вид .

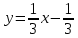e) Необходимо найти длину высоты 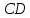. Определим координаты точки – точки пересечения прямых и 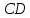– из системы: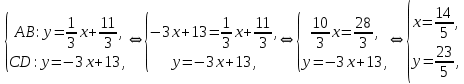



т. е. прямые и 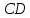пересекаются в точке 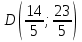. Тогда длина высоты :





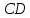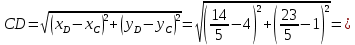
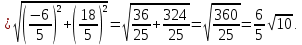
f) Угол – это угол между векторами 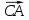и

---

Смотрите также файлы

• Алгебра пні бойынша кнтізбеліктаырыпты жоспар за мерзімді жоспар Алгебра пні 9 сыныбы Аптасына.docx

• Обозначение Наименование.doc

• Тема Преступления против государственной власти, интересов государственной службы и службы в органах местного самоуправления. Часть 2 Решите задачу.docx

• Function функция аты (параметрлер тізімі 1тип) 2тип.pptx

• северный государственный медицинский университет.docx