Файл: Контрольная работа 1 По дисциплине Высшая математика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 19
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Вычислим координаты векторов 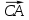 и
и  :
:
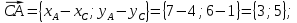
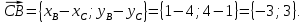
Косинус угла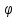 между векторами
между векторами 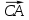 и
и  найдем по формуле:
найдем по формуле:
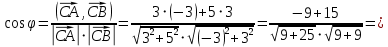
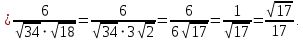
g) Поскольку нам известны длины стороны и высоты
и высоты 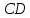 , то площадь треугольника
, то площадь треугольника  вычислим по формуле:
вычислим по формуле:
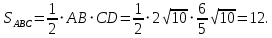
Треугольник и все найденные прямые изображены на рисунке 1.
и все найденные прямые изображены на рисунке 1.
Ответ: a) параметрическое: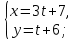 каноническое:
каноническое: 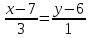 ; общее:
; общее: 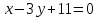 ; с угловым коэффициентом:
; с угловым коэффициентом: 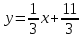 ; в отрезках:
; в отрезках: 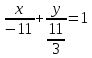 ;
;
b)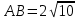 ; c)
; c) 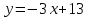 ; d)
; d) 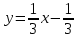 ; e)
; e) 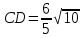 ; f)
; f) 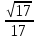 ; g)
; g) 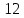 .
.
Задание 4. Дана кривая второго порядка.
a) Приведите кривую второго порядка к каноническому виду.
b) Найдите эксцентриситет кривой.
c) Найдите уравнения директрис.
d) Найдите координаты фокусов кривой.
e) Найдите уравнения асимптот (для гиперболы).
f) Постройте кривую второго порядка, фокусы и директрисы на одном чертеже.
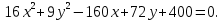
Решение.
Приведем уравнение кривой к каноническому виду:
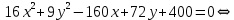
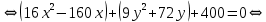
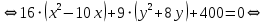
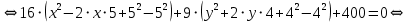
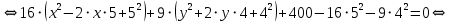
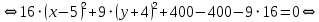
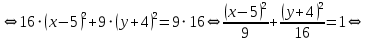
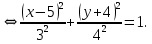
Таким образом, получили каноническое уравнение эллипса с центром в точке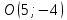 и полуосями
и полуосями 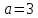 и
и 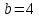 .
.
Вычислим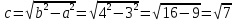 , тогда
, тогда 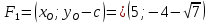 и
и 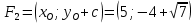 – фокусы,
– фокусы, 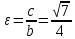 – эксцентриситет.
– эксцентриситет.
Директрисы эллипса:
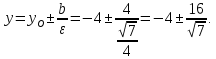
Построим эллипс, его фокусы и директрисы на рисунке 2.
Ответ: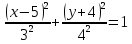 ;
; 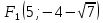 ,
, 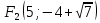 – фокусы;
– фокусы; 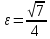 – эксцентриситет;
– эксцентриситет; 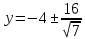 – директрисы.
– директрисы.
Задание 5. Найти пределы функций, не пользуясь правилом Лопиталя.

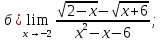
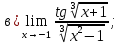

Решение.
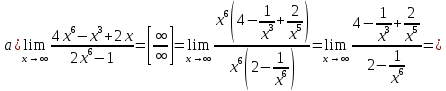
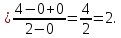
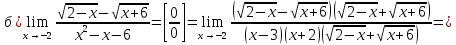
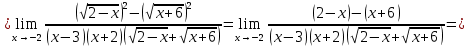
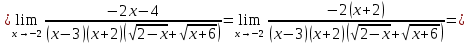
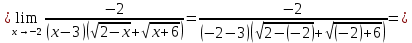
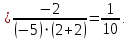
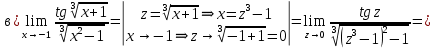
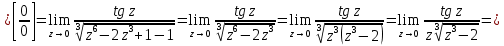
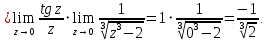
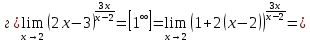
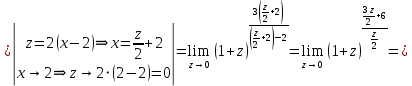
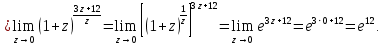
Ответ: а)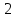 ; б)
; б) 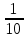 ; в)
; в) 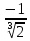 ; г)
; г) 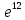 .
.
Задание 6. Задана функция . Найдите точки разрыва функции, если они существуют. Сделайте чертёж.
. Найдите точки разрыва функции, если они существуют. Сделайте чертёж.
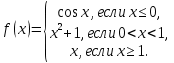
Решение.
Функция непрерывна на интервалах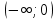 ,
, 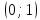 и
и 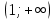 . Исследуем непрерывность функции в точках
. Исследуем непрерывность функции в точках 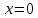 и
и 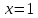 . Для этого вычислим односторонние пределы в этих точках. Начнём с точки
. Для этого вычислим односторонние пределы в этих точках. Начнём с точки 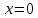 :
:
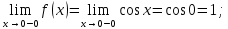
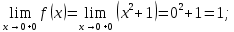
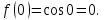
Получили равенство:
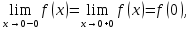
значит, функция непрерывна в точке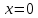 .
.
Аналогично вычислим односторонние пределы в точке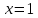 :
:
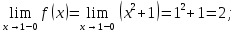
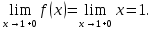
Односторонние пределы в точке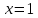 конечны, но не совпадают, значит,
конечны, но не совпадают, значит, 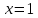 – точка разрыва первого рода.
– точка разрыва первого рода.
На рисунке 3 представлен график функции .
.
Ответ: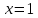 – точка разрыва первого рода.
– точка разрыва первого рода.
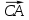 и
и  :
: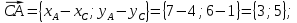
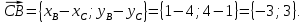
Косинус угла
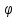 между векторами
между векторами 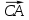 и
и  найдем по формуле:
найдем по формуле: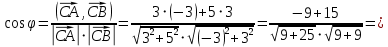
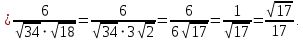
g) Поскольку нам известны длины стороны
 и высоты
и высоты 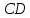 , то площадь треугольника
, то площадь треугольника  вычислим по формуле:
вычислим по формуле: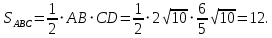
Треугольник
 и все найденные прямые изображены на рисунке 1.
и все найденные прямые изображены на рисунке 1. 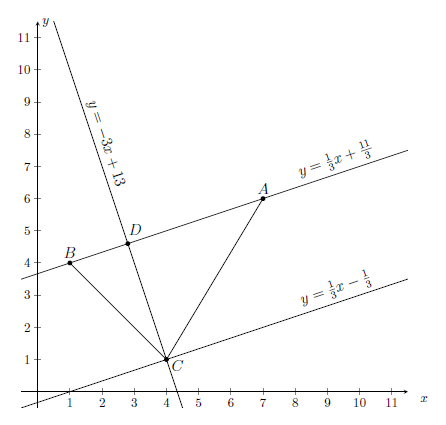 |
| Рисунок 1 – Треугольник  |
Ответ: a) параметрическое:
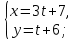 каноническое:
каноническое: 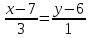 ; общее:
; общее: 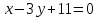 ; с угловым коэффициентом:
; с угловым коэффициентом: 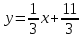 ; в отрезках:
; в отрезках: 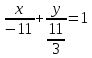 ;
; b)
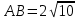 ; c)
; c) 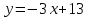 ; d)
; d) 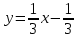 ; e)
; e) 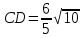 ; f)
; f) 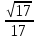 ; g)
; g) 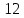 .
.Задание 4. Дана кривая второго порядка.
a) Приведите кривую второго порядка к каноническому виду.
b) Найдите эксцентриситет кривой.
c) Найдите уравнения директрис.
d) Найдите координаты фокусов кривой.
e) Найдите уравнения асимптот (для гиперболы).
f) Постройте кривую второго порядка, фокусы и директрисы на одном чертеже.
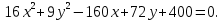
Решение.
Приведем уравнение кривой к каноническому виду:
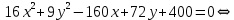
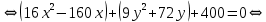
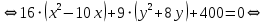
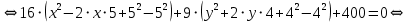
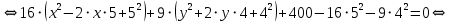
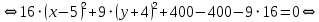
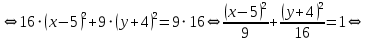
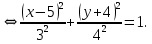
Таким образом, получили каноническое уравнение эллипса с центром в точке
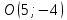 и полуосями
и полуосями 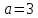 и
и 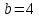 .
.Вычислим
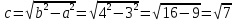 , тогда
, тогда 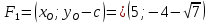 и
и 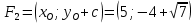 – фокусы,
– фокусы, 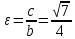 – эксцентриситет.
– эксцентриситет.Директрисы эллипса:
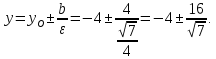
Построим эллипс, его фокусы и директрисы на рисунке 2.
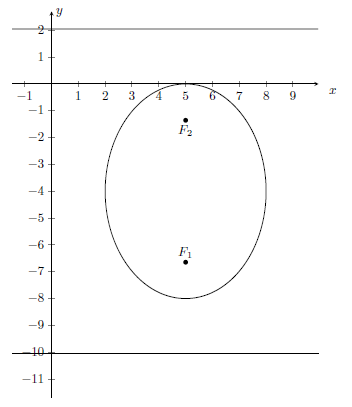 |
| Рисунок 2 – Эллипс 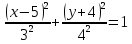 |
Ответ:
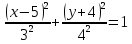 ;
; 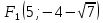 ,
, 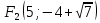 – фокусы;
– фокусы; 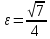 – эксцентриситет;
– эксцентриситет; 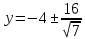 – директрисы.
– директрисы.Задание 5. Найти пределы функций, не пользуясь правилом Лопиталя.

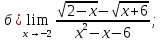
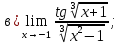

Решение.
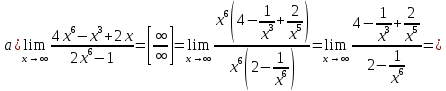
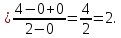
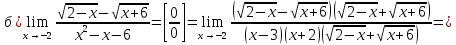
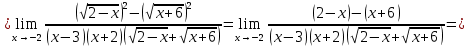
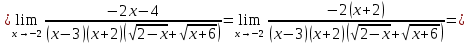
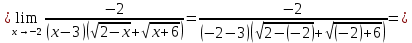
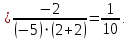
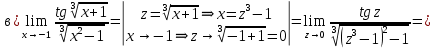
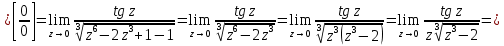
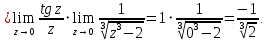
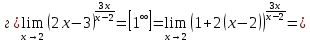
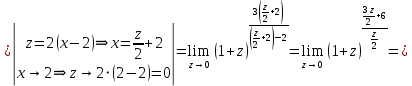
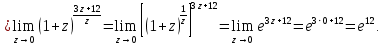
Ответ: а)
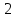 ; б)
; б) 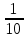 ; в)
; в) 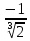 ; г)
; г) 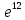 .
.Задание 6. Задана функция
 . Найдите точки разрыва функции, если они существуют. Сделайте чертёж.
. Найдите точки разрыва функции, если они существуют. Сделайте чертёж.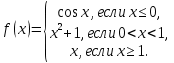
Решение.
Функция непрерывна на интервалах
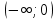 ,
, 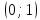 и
и 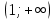 . Исследуем непрерывность функции в точках
. Исследуем непрерывность функции в точках 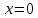 и
и 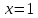 . Для этого вычислим односторонние пределы в этих точках. Начнём с точки
. Для этого вычислим односторонние пределы в этих точках. Начнём с точки 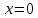 :
: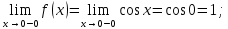
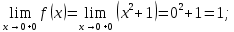
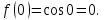
Получили равенство:
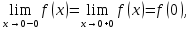
значит, функция непрерывна в точке
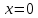 .
.Аналогично вычислим односторонние пределы в точке
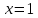 :
: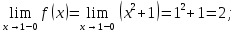
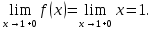
Односторонние пределы в точке
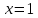 конечны, но не совпадают, значит,
конечны, но не совпадают, значит, 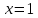 – точка разрыва первого рода.
– точка разрыва первого рода.На рисунке 3 представлен график функции
 .
. 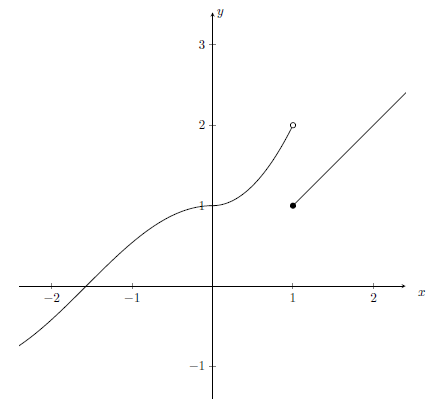 |
| Рисунок 3 – График функции  |
Ответ:
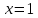 – точка разрыва первого рода.
– точка разрыва первого рода.