Файл: Курсовая работа состоит из введения, двух глав, заключения, списка литературы, приложений. В первой главе рассматриваются алгоритмы сортировки обменом, а именно пузырьковая,.docx
Добавлен: 29.04.2024
Просмотров: 18
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СРАВНИТЕЛЬНЫЙ АНАЛИЗ
АЛГОРИТМОВ СОРТИРОВКИ ОБМЕНАМИ
Цель работы – провести сравнительный анализ сортировок обменом на языке программирования высокого уровня.
Курсовая работа состоит из введения, двух глав, заключения, списка литературы, приложений. В первой главе рассматриваются алгоритмы сортировки обменом, а именно пузырьковая, шейкерная, расчёской, чет–нечет, придурковатая, вялая, туповатая, гномья и быстрая сортировка.
Во второй главе анализируются эти алгоритмы.
Мы разделили сортировки на три группы по такому принципу: первая – асимптотика хуже
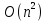, вторая – в среднем 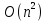, третья – в лучшем случае или в среднем асимптотика 
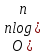)).Сейчас мы рассмотрим сортировки из первой группы. На презентации представлена таблица с тестированием сортировки из первой группы. Как видно из результатов, данные алгоритмы даже на очень небольших данных работают медленно, поэтому далее их мы не рассматривали.
Перейдем ко второй группе сортировок, я выбрал наиболее интересный пример. В этой таблице набором данных послужили массивы почти отсортированные, то есть в них данные располагались так, что достаточно пару десятков элементов поставить на свои места и массив будет отсортирован. Тут произошла ситуация когда преимущество шейкерной сортировки не сработало и она превратилась в пузырьковую.
Далее рассмотрим сравнение третьей группы сортировок со второй. Также выбрал наиболее интересный пример и набор данных почти отсортированный массив. Как видно из таблицы Быстрая сортировка отработала хуже всех. Так как из-за такого расположения элементов рекурсия делит массив на части практически для каждый пары рядом стоящих элементов, что приводит к максимально возможному количеству вызовов рекурсии.
Можно сделать такой вывод
, что в среднем более сложные сортировки имеют значительное преимущество над простыми, но в отдельных задачах иногда требуется простой подход, чтобы получить оптимальный результат. Например, сортировка небольших массивов, почти упорядоченных или наборов данных с небольшим количеством уникальных значений.
Также для наглядности на презентации предоставлены графики сравнения реального времени работы с теоретическим. Из видно, что в принципе теоретичное совпадает с реальным.
