МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра вычислительной техники


Курсовая РАБОТА

по дисциплине «Алгоритмы и структуры данных»

Тема: Графы

Студент гр. 0321		Смолянинов Д.И.
Преподаватель		Манирагена В.

Санкт-Петербург

2023

ЗАДАНИЕ

на курсовую работу

Студент Смолянинов Д.И.
Группа 0321
Тема работы: графы
Исходные данные: количество вершин графа, список рёбер графа
Содержание пояснительной записки: Содержание, введение, теоретическая часть, алгоритм решения задачи, результаты тестирования программы, заключение, список использованных источников, приложение 1 – руководство пользователя, приложение 2 – исходный код программы.
Предполагаемый объем пояснительной записки: Не менее 10 страниц.
Дата выдачи задания: 01.09.2022
Дата сдачи реферата: 13.01.2023
Дата защиты реферата: 13.01.2023
Студент		Смолянинов Д.И.
Преподаватель		Манирагена В.

Аннотация
В данной курсовой работе необходимо разработать программу для работы с графами. Необходимо, чтобы был реализован алгоритм поиска клики наибольшей мощности в неориентированном графе.

Summary
In this course work it is necessary to develop a program for working with graphs. It is necessary to implement an algorithm for finding the largest clique in an undirected graph.

содержание

	Введение	5
1.	Теоретическая часть	6
2.	Алгоритм решения задачи	7
3.	Результаты тестирования программы	8
	Заключение	9
	Список использованных источников	10
	Приложение 1. Руководство пользователя	11
	Приложение 2. Исходный код программы	12

---

введение
В программе, разрабатываемой в ходе курсовой работы, необходимо реализовать алгоритм поиска клики наибольшей мощности в неориентированном графе. Задаётся количество вершин графа и все рёбра, результатом является список номеров вершин, составляющих клику наибольшей мощности.
1. Теоретическая часть
Граф – это математическая абстракция реальной системы любой природы, объекты которой обладают парными связями. Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин, и множества их парных связей, называемого множеством рёбер. Элемент множества рёбер есть пара элементов множества вершин.

Матрица смежности – это представление графа в виде матрицы. Она представляет собой квадратную матрицу размером n*n, в которой значение элемента i, j равно числу рёбер между вершинами i, j.

Клика – это подмножество вершин графа, любые две из которых соединены ребром.
2. Алгоритм решения задачи
Имеется матрица смежности графа. Для каждой новой строки первый элемент добавляется в текущую клику. Затем анализируются следующие после соответствующей строке вершины на смежность с другими вершинами текущей клики. Если текущая вершина прошла проверку, она добавляется в текущую клику.

В клике не может быть меньше 2 вершин. Если в текущую клику не добавлялось вершин, она не становится максимальной ни в каком случае. Иначе проверяется, больше ли эта клика по размеру текущей максимальной. Если так, текущая становится максимальной.

После анализа всей матрицы смежности выводится максимальная клика, если в графе существует хоть одна клика.
3. Результаты тестирования программы


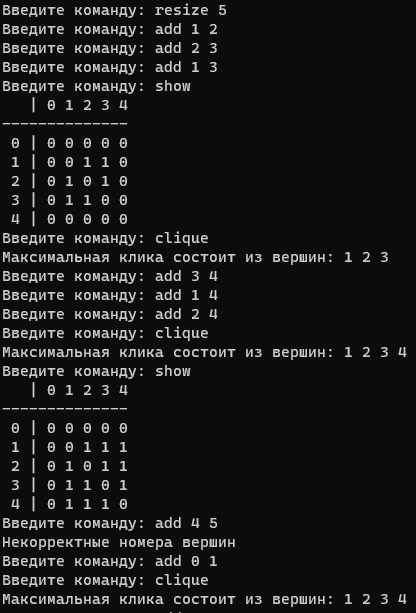
Рисунок 1: результат работы программы
В результате работы программа вывела клики наибольшей мощности в зависимости от состояния графа.
заключение
В результате выполнения данной курсовой работы была написана программа, реализующая алгоритм поиска клики наибольшей мощности в неориентированном графе, изучены способы представления графа в памяти ЭВМ.

---

список использованных источников
1. Колинько П.Г. Пользовательские структуры данных. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2020. с.

2. Википедия. URL: https://ru.wikipedia.org (дата обращения: 05.01.2023).

приложение 1

РУководство пользователя
Команды:
create – создать граф. После этого необходимо задать количество вершин.

add – добавить ребро. После этого необходимо задать 2 вершины, между которыми будет построено ребро.

clear – очистить граф от рёбер.

clique – вывести максимальную клику.

remove – удалить граф.

show – вывести граф на экран.

exit – выйти из программы.

приложение 2

исходный код программы
CourseWork-ADS.cpp

#include
#include

#include
#include "Graph.h"
using namespace std;
const string ADD_COMMAND = "add";

const string REMOVE_COMMAND = "remove";

const string CLEAR_COMMAND = "clear";

const string RESIZE_COMMAND = "resize";

const string SHOW_COMMAND = "show";

const string CLIQUE_COMMAND = "clique";

const string GETHELP_COMMAND = "help";

const string EXIT_COMMAND = "exit";
int main() {

setlocale(LC_ALL, "Russian");

SetConsoleCP(1251);

SetConsoleOutputCP(1251);
Graph *graph = new Graph();
string command;
while (true) {

cout << "Введите команду: ";

cin >> command;
if (command == ADD_COMMAND) {

int first, second;

cin >> first >> second;

graph->add(first, second);
} else if (command == REMOVE_COMMAND) {

int first, second;

cin >> first >> second;

graph->remove(first, second);
} else if (command == CLEAR_COMMAND) {

graph->clear();
} else if (command == RESIZE_COMMAND) {

int newSize;

cin >> newSize;

graph->resize(newSize);
} else if (command == SHOW_COMMAND) {

graph->show();
} else if (command == CLIQUE_COMMAND) {

graph->getMaxClique();
} else if (command == GETHELP_COMMAND) {

cout << "add <первая_вершина> <вторая_вершина> - добавить связь между "

"двумя вершинами\n"

<< "remove <первая_вершина> <вторая_вершина> - удалить связь между "

"двумя вершинами\n"

<< "clear - очистить граф\n"

<< "resize <количество_вершин> - переконструировать граф под "

"заданное количество вершин\n"

<< "show - вывести граф на экран в виде матрицы\n"

<< "clique - отыскать наибольшую клику в графе\n"

<< "help - помощь\n"

<< "exit - выход" << endl;
} else if (command == EXIT_COMMAND) {

break;
} else {

cout << "Введите корректную команду" << endl;

}

}
delete graph;

}
Graph.h

#pragma once
#include

#include

#include

#include
using namespace std;
class Graph {

private:

int size_;

int **matrix_;
bool verticlesIsValid(int first, int second);
public:

Graph();

Graph();
void add(int first, int second);

void remove(int first, int second);

void clear();

void resize(int newSize);

void show() const;

void getMaxClique() const;

};

Graph.cpp

#include "Graph.h"
bool Graph::verticlesIsValid(int first, int second) {

return first >= 0 && second >= 0 && first < size_ && second < size_ &&

first != second;

}
Graph::Graph() : size_(0), matrix_(nullptr) {}
Graph::Graph() { resize(0); }
void Graph::add(int first, int second) {

if (verticlesIsValid(first, second)) {

matrix_[first][second] = 1;

matrix_[second][first] = 1;

} else {

cout << "Некорректные номера вершин" << endl;

}

}
void Graph::remove(int first, int second) {

if (verticlesIsValid(first, second)) {

matrix_[first][second] = 0;

matrix_[second][first] = 0;

} else {

cout << "Некорректные номера вершин" << endl;

}

}
void Graph::clear() {

if (size_ != 0) {

for (int i = 0; i < size_; ++i) {

for (int j = 0; j < size_; ++j) {

matrix_[i][j] = 0;

}

}

}

}
void Graph::resize(int newSize) {

if (newSize >= 0) {

if (newSize != size_) {

clear();
size_ = newSize;
if (size_ > 0) {

matrix_ = new int *[size_];

for (int i = 0; i < size_; ++i) {

matrix_[i] = new int[size_]{};

}

}

} else if (newSize == 0) {

for (int i = 0; i < size_; ++i) {

delete[] matrix_[i];

}
delete[] matrix_;

matrix_ = nullptr;
size_ = newSize;

}

} else {

cout << "Некорректный размер графа" << endl;

}

}
void Graph::show() const {

if (size_ > 0) {

int fieldWidth = (int)log10(size_ - 1) + 2;

int lineLength = fieldWidth * (size_ + 1) + 2;
cout << setw(fieldWidth) << "" << " |";
for (int i = 0; i < size_; ++i) {

cout << setw(fieldWidth) << i;

}

cout << endl;
for (int i = 0; i < lineLength; ++i) {

cout << '-';

}

cout << endl;
for (int i = 0; i < size_; ++i) {

cout << setw(fieldWidth) << i;

cout << " |";
for (int j = 0; j < size_; ++j) {

cout << setw(fieldWidth) << matrix_[i][j];

}

cout << endl;

}

}

}
void Graph::getMaxClique() const {

vector *maxClique = new vector(); //последняя максимальная клика

vector *currentClique = new vector(); //текущая клика
for (int i = 0; i < size_; ++i) {

currentClique->push_back(i); //с текущей вершины начинается новая клика
for (int j = i + 1; j < size_; ++j) { //поиск нового кандидата для клики

bool adjacencyForAll = true;

//смежность кандидата с остальными текущими вершинами
//в следующем цикле проверяется, есть ли отсутствие смежности

//с хотя бы одной из вершин текущей клики

for (auto it = currentClique->begin(); it != currentClique->end(); ++it) {

if (matrix_[j][*it] == 0) {

adjacencyForAll = false;

//смежность отсутствует, кандидат не добавляется

}

}
if (adjacencyForAll) {

//если кандидат смежен с другими вершинами, он добавляется в клику

currentClique->push_back(j);

}

}
if (currentClique->size() > 1 &&

maxClique->size() < currentClique->size()) {

//в каждой клике должно быть 2 вершины. Иначе currentClique не

//обрабатывается

//если новая клика больше последней максимальной

//скопировать её содержимое в переменную максимальной клики

maxClique->clear();

for (auto it = currentClique->begin(); it != currentClique->end(); ++it) {

maxClique->push_back(*it);

}

}

currentClique->clear();

}
delete currentClique;
//вывод максимальной клики

if (maxClique->size() > 0) {

sort(maxClique->begin(), maxClique->end());

cout << "Максимальная клика состоит из вершин: ";

for (auto it = maxClique->begin(); it != maxClique->end(); ++it) {

cout << *it << " ";

}

cout << endl;

}
delete maxClique;

}

---

Смотрите также файлы

• Баяндама таырыбы.docx

• Тестовые вопросы по смп и неотложки бригада смп получила вызов по рации с формулировкой Без сознания на улице неизвестный мужчина.docx

• Контрольная работа по теме Имя существительное.docx

• А Оушылара за білімі саласынан малмат беру з ытарын жете білуге, з беттерімен салыстыра білуге, мірде олдана білуге йрету ыты білімдерін толытыру.docx

• Разработка, анализ и оценка управляющих решений финансового менеджера.docx