Задание 4. При поверке вольтметра определили, что показания образцового вольтметра U₀= 1 В, а поверяемого U= 0.95 В. Определите абсолютную по­грешность и поправку для поверяемого прибора.
Абсолютная погрешность определяется по формуле:

,

где x – результат измерения;

– действительное значение измеряемой величины (показания образцового вольтметра).

Таким образом, абсолютная погрешность будет равна:

В.

Поправка определяется как величина, обратная по знаку абсолютной погрешности, т.е. поправка будет равна:

В.
Задание 5. Найдите относительную погрешность вольтметра класса точности 1.0 с диапазоном измерении от 0 до 150 В, в точке шкалы 50 В. Запишите ре­зультат измерения.
Относительная погрешность связана с приведенной следующей формулой:

,

где - приведенная погрешность, определяемая классом точности;

- диапазон (длина) шкалы;

- значение измерений.

Вычислим относительную погрешность:

.

Для записи результата измерений необходимо найти абсолютную погрешность. Она связана с приведенной следующим соотношением:

---

В.

Также ее можно вычислить, зная относительную погрешность:

В.

Полученная величина погрешности не нуждается в округлении, так как первая значащая цифра меньше 3 (равна 1) и, следовательно, оставляем две значащие цифры.

Результат измерения необходимо представить со степенью точности погрешности, и он примет вид 50,0 В.

В итоге результат измерения напряжения в стандартной форме будет иметь вид:

В.

3 Контрольная работа №3
Задание 1. Для определения пройденного телом пути измерялись скорость его пе­ремещения и время. Были получены следующие результаты: v=(59.8±0.2) км/час; t=(3.1±0.1) мин. Определите расстояние, пройденное телом, и оце­ните погрешность измерения.
Пройденное расстояние вычисляется по формуле:

.

При косвенных измерениях, когда известны функция и предельные по­грешности измерения аргументов, используется зависимость для определе­ния предельной погрешности измерения искомой величины (функции):



где k – число измеряемых аргументов;

– частные производные или коэффициенты влияния аргументов на искомую величину;

– предельные абсолютные погрешности измерений соответствую­щих аргументов.

Используя данное соотношение, найдем выражение для величины погрешности пройденного телом расстояния:

.

Для вычисления пройденного пути необходимо перевести скорость в м/с, а время в секунды.

Чтобы перевести величину скорости и ее погрешность в м/с необходимо разделить имеющиеся значения в км/ч на 3,6. В итоге получим:

---

км/ч м/с м/с;

км/ч м/с м/с;

Чтобы перевести время в секунды, необходимо имеющиеся значения в минутах умножить на 60:

мин. с. с.

мин. с. с.

Подставив числовые значения, вычислим погрешность пройденного пути:

м.

Определим величину пройденного пути:

м.

Теперь необходимо округлить погрешность. Так как первая значащая цифра меньше 3 (равна 1), то оставляем две значащие цифры. Цифра старшего отбрасываемого разряда меньше 5 (равна 0), поэтому последняя сохраняемая цифра числа остается без изменений. В итоге получим погрешность 110 м.

Пройденное расстояние округляем до степени точности погрешности и в итоге получим 3090 м. Последнюю сохраняемую цифру увеличили на единицу, так как цифра старшего отбрасываемого разряда старше 5 (равна 9).

Границы истинного значения пройденного пути будут иметь вид:

м.
Задание 2. При многократном измерении массы m получены значения, кг: 98; 100; 97; 104; 99; 102; 103; 112; 96; 105; 97; 102; 99; 101; 100. Обработай­те результаты измерений и укажите доверительные границы для истинного значения массы с вероятностью Р_д = 0.80.
Вычислим среднее арифметическое значение результатов измерений массы и принимаем его за результат измерений:

---

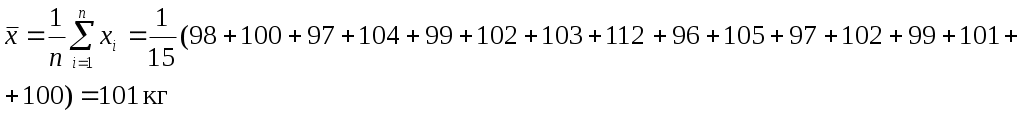Следующим этапом является вычисление оценки среднеквадратического отклонения по формуле:

.

Для удобства расчета создадим таблицу.

104	3	9
99	-2	4
102	1	1
103	2	4
112	11	121
96	-5	25
105	4	16
97	-4	16
102	1	1
99	-2	4
101	0	0
100	-1	1
104	3	9
99	-2	4
102	1	1
		=228

В итоге оценка среднеквадратического отклонения будет равна:

.

Далее необходимо оценить наличие промахов в результатах измерений.

Количество измерений равно 15, поэтому можно использовать критерий Романовского.

Согласно критерию вычисляют отношение:

.

Полученный результат сравнивают с табличным на принятом уровне значимости и если расчетное значение превышает табличное, то результат является промахом.

---

В нашем случае сомнительными результатами измерений могут быть наибольшее 112 и наименьшее 96. Вычислим для них критерий Романовского:

; и .

Табличное значение на уровне значимости 0,05: .

Критерий Романовского для значения 112 превышает табличное (2,72>2,64), следовательно, оно является промахом на принятом уровне значимости. Его необходимо исключить и заново повторить вычисления.

Вычислим среднее арифметическое значение результатов измерений массы исключив ошибочный результат измерений:

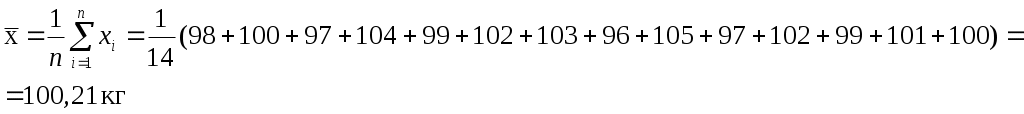Снова вычислим оценку среднеквадратического отклонения создав аналогичную таблицу.

104	3,79	14,33
99	-1,21	1,47
102	1,79	3,19
103	2,79	7,76
96	-4,21	17,76
105	4,79	22,90
97	-3,21	10,33
102	1,79	3,19
99	-1,21	1,47
101	0,79	0,62
100	-0,21	0,05
104	3,79	14,33
99	-1,21	1,47
102	1,79	3,19
		=98,36

---

Смотрите также файлы

• На основании выбранного варианта выполнить следующее.docx

• Контрольная работа по дисциплине бжд вариант 11 студент группы бсб (до)з151(цдо).doc

• Мектеп Н. Одасынов атындаы жом.docx

• Воспитательные задачи.docx

• О прохождении Учебнойпрактики.docx