Файл: Перечень вопросов по дисциплине Теория информационных процессов и систем.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 49
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, что сказывается на результатах экспертизы.
Методы типа дерево целей
Термин “дерево целей” означает наличие у рассматриваемой системы иерархической структуры, у которой можно выделить общую цель, подцели, функции и т.д.
Наиболее широко данный метод применяется для систем, для которых характерен строгий порядок (иерархия). При анализе целей научных исследований целесообразно говорить о дереве направлений прогнозирования. При использовании термина “прогнозный граф” появляется возможность определения дерева как связанного ориентированного графа, не содержащего петель, каждая пара вершин которого соединена единственной целью.
SCADA–СИСТЕМЫ
Это информационные системы дистанционного управления сбора данных.
ОБЛАСТЬ ПРИМЕНЕНИЯ
Атомная промышленность, атомная энергетика, электроэнергетика, все виды транспорта, все виды связи и т.д.
ПРЕИМУЩЕСТВЕННЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ
цеховой уровень автоматизации. Он связан с получением и визуализацией информации от программных микроконтроллеров распространенных систем управления.
ФУНКЦИОНАЛЬНОЕ НАЗНАЧЕНИЕ
мониторинг – сбор и оценка данных технического процесса;
управление параметрами технического процесса;
осуществление обратной связи входных и выходных данных в автоматическом режиме;
прием информации о контролируемых технологических параметрах от контролеров нижнего уровня;
сохранение принятой информации в архивах;
вторичная обработка принятой информации;
графическое отображение хода технологического процесса;
прием команд оператора и их передача в адрес контролера нижнего уровня;
регистрация события, связанная с контролируемым технологическим процессом и действиями персонала ответственного за эксплуатацию;
оповещение об аварийных ситуациях и функционировании программного обеспечения;
формирование сводок и других отчетных документаций на основе архивной и текущей документаций;
обмен информацией с внешними системами управления предприятий;
реализация автономного управления технологическим процессом по заданному алгоритму.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ SCADA–СИСТЕМ
–Имеющиеся средства сетевой поддержки.
–Встроенные командные языки.
–Поддерживаемые базы данных.
–Графические возможности.
Основные функции могут быть реализованы простейшим случаем на базе одной простейшей ЭВМ. При управлении сложными техническими процессами SCADA-системы включают сеть ЭВМ с центральным пультом управления, переферийные устройства и средства связи.


1–физический процесс,
2–мониторинг
Мониторинг – одна из базовых функций SCADA-систем.
Типы мониторинга:
1. сбор первичной информации и отображение ее на экране;
2. проведение предварительного анализа с целью проверки нахождения результатов проверки в допустимых пределах.
Режим, при котором функция системы ограничена сбором и отображением результатов, а решение об управляющих действиях принимает оператор, наз. супервизорным (дистанционным).
3–анализ и отображение информации,
4–оператор,
5–дистанционное управление,
6–управление,
7–регулирование.
В SCADA-системах различают инструментальное и прикладное программное обеспечение.
Недостатки инструментального программного управления:
–наличие не выявленных ошибок на этапе проектирования.
–не возможность устранения таких ошибок сотрудниками предприятия без привлечения разработчиков.
ПЕРИОДИЧЕСКИЙ СИГНАЛ
Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой.
ЛИНЕЙНЫЙ СПЕКТР

Рис. 2.4. Спектр периодической функции
Спектр периодической функции состоит из отдельных "линий", соответствующих дискретным частотам:
0, ω, 2 ω,…, n ω. Отсюда и название — линейчатый, или дискретный, спектр. a0/2 – постоянная составляющая, An – амплитуда n–ой гармоники, ω = 2π/T, T – период.
Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы.Случайным сигналом мы будем называть сигнал, математическим описанием которого является случайная Функция времени. Характеристики таких сигналов являются статистическими, то есть имеют вероятностный вид.
Существует 2 основных класса случайных сигналов:
–шумы,
–случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
СЛУЧАЙНЫЙ ПРОЦЕСС
в его математическом описании Х(t) представляет собой функцию, которая отличается тем, что ее значения (действительные или комплексные) в произвольные моменты времени по координате t являются случайными.
КОВАРИАЦИОННЫЕ ФУНКЦИИ
Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений случайной функции в моменты времени ti и tj и характеризует флуктуационную (отклонение значения от среднего, от точки равновесия) составляющую процесса.
В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции автокорреляции.
Автокорреляция — это взаимосвязь последовательных элементов временного или пространственного ряда данных.
ГАУССОВСКИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом. Одномерная плотность вероятности нормального процесса определяется выражением:

где δx – среднеквадратическое отклонение, mx – математическое ожидание.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
представляет собой статистическое усреднение случайной величины X(ti) в каком либо фиксированном сечении ti случайного процесса, т. е. среднее арифметическое суммы X(ti) при i=1,2,…,n.
СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Рассеивания значений случайной величины относительно её математического ожидания.
СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ
функция, задающая распределение мощности сигнала по частотам. Её значение имеет размерность мощности, делённой на частоту, то есть энергии.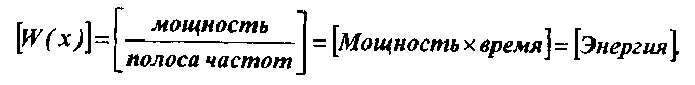
Полоса пропускания – диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.
Неравномерность АЧХ характеризует степень отклонения от прямой, параллельной оси частот. Неравномерность АЧХ выражается в децибелах.
Ослабление неравномерности АЧХ в полосе улучшает воспроизведение формы передаваемого сигнала.
ИДЕАЛЬНЫЙ КАНАЛ
Модель идеального канала используется тогда, когда можно пренебречь наличием помех. При использовании этой модели выходной сигнал является детерминированным, мощность и полоса пропускания сигналов ограниченны.
Детерминированный сигнал точно определен в любой момент времени.
Полоса пропускания это разность между максимальной и минимальной частотами сигнала.
РЕАЛЬНЫЙ КАНАЛ
В реальных каналах всегда имеются ошибки при передаче сообщений. Ошибки приводят к уменьшению пропускной способности канала и потере информации. Вероятности появления ошибок во многом определяются искажениями сигналов и влиянием помех.
Сигнал на выходе канала можно записать в следующем виде:
x(t) = μ(t)∙s(t-T)+w(t),
где s(t) – сигнал на входе канала, w(t) – аддитивная помеха, μ(t) – мультипликативная помеха, T – задержка сигнала.
Аддитивная помеха – помеха, прибавляемая к сигналу при передаче его по информационному каналу.
Аддитивные помехи обусловлены флуктуационными явлениями (случайными колебаниями тока и напряжения), связанными с тепловыми процессами в проводах, резисторах, транзисторах и других элементах схем, наводками под действием атмосферных явлений (грозовые разряды ит. д.) и индустриальных процессов (работа промышленных установок, других линий связи и т. д.).
Методы типа дерево целей
Термин “дерево целей” означает наличие у рассматриваемой системы иерархической структуры, у которой можно выделить общую цель, подцели, функции и т.д.
Наиболее широко данный метод применяется для систем, для которых характерен строгий порядок (иерархия). При анализе целей научных исследований целесообразно говорить о дереве направлений прогнозирования. При использовании термина “прогнозный граф” появляется возможность определения дерева как связанного ориентированного графа, не содержащего петель, каждая пара вершин которого соединена единственной целью.
-
Область применения, функциональное назначение и основные технические характеристики SCADA-систем.
SCADA–СИСТЕМЫ
Это информационные системы дистанционного управления сбора данных.
ОБЛАСТЬ ПРИМЕНЕНИЯ
Атомная промышленность, атомная энергетика, электроэнергетика, все виды транспорта, все виды связи и т.д.
ПРЕИМУЩЕСТВЕННЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ
цеховой уровень автоматизации. Он связан с получением и визуализацией информации от программных микроконтроллеров распространенных систем управления.
ФУНКЦИОНАЛЬНОЕ НАЗНАЧЕНИЕ
мониторинг – сбор и оценка данных технического процесса;
управление параметрами технического процесса;
осуществление обратной связи входных и выходных данных в автоматическом режиме;
прием информации о контролируемых технологических параметрах от контролеров нижнего уровня;
сохранение принятой информации в архивах;
вторичная обработка принятой информации;
графическое отображение хода технологического процесса;
прием команд оператора и их передача в адрес контролера нижнего уровня;
регистрация события, связанная с контролируемым технологическим процессом и действиями персонала ответственного за эксплуатацию;
оповещение об аварийных ситуациях и функционировании программного обеспечения;
формирование сводок и других отчетных документаций на основе архивной и текущей документаций;
обмен информацией с внешними системами управления предприятий;
реализация автономного управления технологическим процессом по заданному алгоритму.
ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ SCADA–СИСТЕМ
–Имеющиеся средства сетевой поддержки.
–Встроенные командные языки.
–Поддерживаемые базы данных.
–Графические возможности.
-
Структурные элементы, системное программное обеспечение SCADA-систем.
Основные функции могут быть реализованы простейшим случаем на базе одной простейшей ЭВМ. При управлении сложными техническими процессами SCADA-системы включают сеть ЭВМ с центральным пультом управления, переферийные устройства и средства связи.


1–физический процесс,
2–мониторинг
Мониторинг – одна из базовых функций SCADA-систем.
Типы мониторинга:
1. сбор первичной информации и отображение ее на экране;
2. проведение предварительного анализа с целью проверки нахождения результатов проверки в допустимых пределах.
Режим, при котором функция системы ограничена сбором и отображением результатов, а решение об управляющих действиях принимает оператор, наз. супервизорным (дистанционным).
3–анализ и отображение информации,
4–оператор,
5–дистанционное управление,
6–управление,
7–регулирование.
В SCADA-системах различают инструментальное и прикладное программное обеспечение.
Недостатки инструментального программного управления:
–наличие не выявленных ошибок на этапе проектирования.
–не возможность устранения таких ошибок сотрудниками предприятия без привлечения разработчиков.
-
Периодические сигналы. Понятие о линейчатом спектре.
ПЕРИОДИЧЕСКИЙ СИГНАЛ
Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой.
ЛИНЕЙНЫЙ СПЕКТР

Рис. 2.4. Спектр периодической функции
Спектр периодической функции состоит из отдельных "линий", соответствующих дискретным частотам:
0, ω, 2 ω,…, n ω. Отсюда и название — линейчатый, или дискретный, спектр. a0/2 – постоянная составляющая, An – амплитуда n–ой гармоники, ω = 2π/T, T – период.
-
Случайные сигналы и их аналитическое описание.
Случайные сигналы — сигналы, мгновенные значения которых (в отличие от детерминированных сигналов) не известны, а могут быть лишь предсказаны с некоторой вероятностью, меньшей единицы.Случайным сигналом мы будем называть сигнал, математическим описанием которого является случайная Функция времени. Характеристики таких сигналов являются статистическими, то есть имеют вероятностный вид.
Существует 2 основных класса случайных сигналов:
–шумы,
–случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.
-
Понятие о ковариационной функции случайного процесса.
СЛУЧАЙНЫЙ ПРОЦЕСС
в его математическом описании Х(t) представляет собой функцию, которая отличается тем, что ее значения (действительные или комплексные) в произвольные моменты времени по координате t являются случайными.
КОВАРИАЦИОННЫЕ ФУНКЦИИ
Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений случайной функции в моменты времени ti и tj и характеризует флуктуационную (отклонение значения от среднего, от точки равновесия) составляющую процесса.
В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции автокорреляции.
Автокорреляция — это взаимосвязь последовательных элементов временного или пространственного ряда данных.
-
Гауссовский случайный процесс.
ГАУССОВСКИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом. Одномерная плотность вероятности нормального процесса определяется выражением:

где δx – среднеквадратическое отклонение, mx – математическое ожидание.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
представляет собой статистическое усреднение случайной величины X(ti) в каком либо фиксированном сечении ti случайного процесса, т. е. среднее арифметическое суммы X(ti) при i=1,2,…,n.
СРЕДНЕКВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ
Рассеивания значений случайной величины относительно её математического ожидания.
-
Спектральная плотность мощности случайного процесса.
СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ
функция, задающая распределение мощности сигнала по частотам. Её значение имеет размерность мощности, делённой на частоту, то есть энергии.
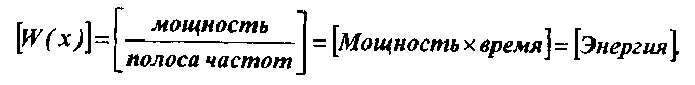
Полоса пропускания – диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.
ОСНОВНЫЕ ПАРАМЕТРЫ ПОЛОСЫ ПРОПУСКАНИЯ
Ширина полосы
Ширина полосы обычно определяется как разность верхней и нижней граничных частот участка АЧХ. Ширина полосы пропускания выражается в единицах частоты (например, в Гц). Расширение полосы пропускания позволяет передать большее количество информации.
Неравномерность АЧХ
Неравномерность АЧХ характеризует степень отклонения от прямой, параллельной оси частот. Неравномерность АЧХ выражается в децибелах.
Ослабление неравномерности АЧХ в полосе улучшает воспроизведение формы передаваемого сигнала.
-
Идеальные и реальные модели канала передачи информации.
ИДЕАЛЬНЫЙ КАНАЛ
Модель идеального канала используется тогда, когда можно пренебречь наличием помех. При использовании этой модели выходной сигнал является детерминированным, мощность и полоса пропускания сигналов ограниченны.
Детерминированный сигнал точно определен в любой момент времени.
Полоса пропускания это разность между максимальной и минимальной частотами сигнала.
РЕАЛЬНЫЙ КАНАЛ
В реальных каналах всегда имеются ошибки при передаче сообщений. Ошибки приводят к уменьшению пропускной способности канала и потере информации. Вероятности появления ошибок во многом определяются искажениями сигналов и влиянием помех.
Сигнал на выходе канала можно записать в следующем виде:
x(t) = μ(t)∙s(t-T)+w(t),
где s(t) – сигнал на входе канала, w(t) – аддитивная помеха, μ(t) – мультипликативная помеха, T – задержка сигнала.
Аддитивная помеха – помеха, прибавляемая к сигналу при передаче его по информационному каналу.
Аддитивные помехи обусловлены флуктуационными явлениями (случайными колебаниями тока и напряжения), связанными с тепловыми процессами в проводах, резисторах, транзисторах и других элементах схем, наводками под действием атмосферных явлений (грозовые разряды ит. д.) и индустриальных процессов (работа промышленных установок, других линий связи и т. д.).

