4.Порядок исследования

1. 
   Ознакомиться с целью, задачами работ и моделью.
   
2. 
   Получить варианты исследования (табл.1).
   
3. 
   Подготовить исходные данные согласно табл.2 и заготовить табл.3 и 4 для занесения результатов расчета.
   
4. 
   Для варианта «охлаждения пластины конвекцией» взять программу из файла «Лабораторные работы по МТ» / лабораторные работы №1 / ПЗ pas. Открыть ее с помощью turbo.exe.
   
5. 
   Для варианта охлаждения путем излучения брать программу П5pas.
   
6. 
   Ввести исходные данные варианта для среднего значения варьируемого параметра в программу значения S, T_o, α, или ε (если программа П5pas), подобрать ∆p и t_k, производя пробные запуски программы F₁₀ – run - enter.
   
7. 
   Построить кривые охлаждения Т_оси(t,0), T (t, 0.5*S) и T_нов (t,S), на (рис.6), используя данные табл.3. Пример рис.6 показан ниже.
   

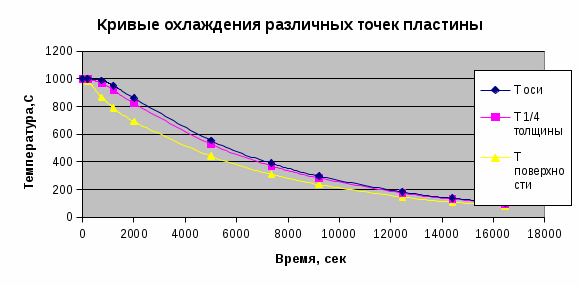
Рис. 6.

8. 
   Построить на рис.7 распределение температуры по толщине пластины, используя данные табл.4. Пример рис.7 показан ниже.
   

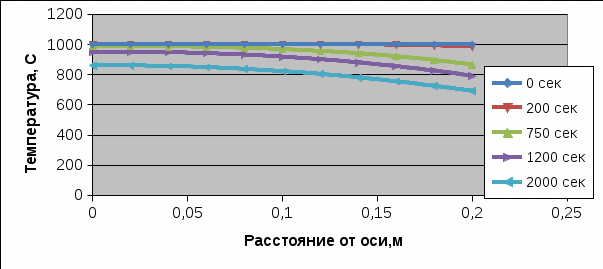
Рис.7. Распределение температуры по толщине пластины для 5-и моментов времени.

9. 
   Определить продолжительность охлаждения пластины до значения температуры оси 100 ⁰С (t¹⁰⁰) для трех значений варьируемого параметра ,построив график с тремя кривыми охлаждения оси пластины.
   

Занести значения варьируемого параметра и соответствующие значения продолжительности охлаждения t¹⁰⁰в табл. 5, пример которой приведен ниже.

Таблица 5. Сводная таблица результатов определения времени охлаждения пластины до 100 °С при различных значениях параметра, например П=25, и результатов расчета по формуле (9).

2S,м – толщина пластины	t100, сек	t100, мин	t100, час	t100, час, формула (6)
0,1	30000	500	8,33	8,38
0,2	67100	1120	18,64	19,40
0,4	161420	2690	44,84	44,88

---

10. 
    Полученные данные по времени охлаждения аппроксимировать формулой :
    

t_охл =a* (П)ⁿ (6)

где П – варьируемый параметр , например, П = 2^.S, T₀,α или ε.

Коэффициенты формулы найдем, подставляя в формулу данные табл.5 (строки 1 и 3), например, П=2^.S

t¹⁰⁰ =a*(2S₁)ⁿ,
t¹⁰⁰ =a*(2S₃)ⁿ.
Решая полученную систему уравнений, получим формулы для определения 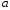, n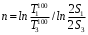



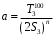
Рассчитаем n и 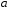для приведенного примера, используя данные таблицы 5.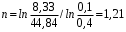





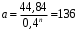
Рассчитаем время охлаждения по формуле (9) при полученных n и 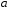и запишем в таблицу 5.

11. 
    Построить зависимость по данным, полученным в табл.5, и по формуле (рис.6).На рисунке 8 изображен пример зависимости времени охлаждения пластины от толщины (2S), полученной по модели и по формуле (9).
    

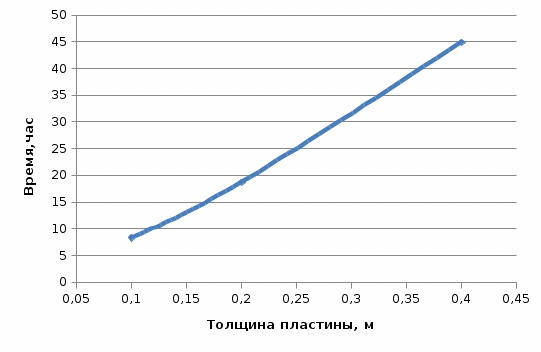
х – из таблицы 5, ------ - формула (6).

Рис. 8 - Зависимость времени охлаждения изделия от толщины пластины до 100 °С.

12. 
    Сформулировать выводы о сделанной работе о полученных закономерностях охлаждения изученного объекта и о практической значимости полученной зависимости.
    
13. 
    Написать отчет по работе.
    

Содержание отчета

1. 
   Титульный лист оформляется в соответствии с правилами, принятыми в ЧГУ, и содержат номер варианта задания.
   
2. 
   Цель и задачи работы.
   
3. 
   Таблица исходных данных (табл.2)
   
4. 
   Таблица результатов расчета температуры Т_оси (t,0), (t,1/2S) , T_нов (t,S) для различных значений времен и (табл.3).
   
5. 
   Рис.6 с кривыми охлаждения 3-х точек температуры во времени , используя табл.3,дать анализ кривых.
   
6. 
   Таблица результатов расчета распределения температуры по толщине пластины ( узлы №№1.3.5.7.9.11) для 5 значений времени 0,1/8t_k, 1/4 t_k,1/2 t_k и t_k(табл.4).
   
7. 
   Рис.7 с распределением температуры по толщине пластины для пяти моментов времени, используя данные табл.4. Дать анализ динамики характера распределения.
   
8. 
   Таблица 5 с результатами расчета продолжительности охлаждения пластины для трех значений варьируемого параметра в заданном варианте.
   
9. 
   Формула t¹⁰⁰ = a (П)ⁿ.
   
10. 
    Рис.8 со сравнением результатов расчета в табл.5 и по формуле.
    
11. 
    Выводы по работе. Например: Выполнено исследование влияния охлаждения конвекцией на продолжительность охлаждения пластины толщиной 0,4м до температуры 100°С. Результаты исследований аппроксимированной формулой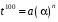 , где =237, n=0,1 и могут быть использованы при определении продолжительности охлаждения плоского изделия до 100°С для =250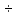 1000Вт/м²к.
    

---

Контрольные вопросы:

1. 
   Написать одномерное уравнение теплопроводности для пластины.
   
2. 
   Написать пример начального условия.
   
3. 
   Написать граничное условие – условие симметрии поля температуры по толщине пластины.
   
4. 
   Граничное условие III рода.
   
5. 
   Граничное условие при охлаждении путем измерения.
   
6. 
   Шаг выдачи на экран.
   
7. 
   Как производится пространственная дискретизация (понятие КХ) в МКР?
   
8. 
   Как производится дискретизация по времени (понятие t)?
   
9. 
   Как выглядит кривая охлаждения оси пластины?
   
10. 
    Как выглядит кривая охлаждения поверхности пластины?
    
11. 
    Как определяется продолжительность охлаждения пластины до 200°С?
    

Литература:

1. 
   Кабаков З.К. и др. Технология математического моделирования металлургических процессов. Курс лекций: учебное пособие. – Череповец: ЧГУ, 2013.-75с.
   

Лабораторная работа №3 Расчет расходов воды на секции зоны вторичного охлаждения
Цель работы: Рассчитать расход воды на секции зоны вторичного охлаждения (ЗВО) МНЛЗ при заданной температурном режиме охлаждения заготовки в ЗВО

Задачи работы:

• 
  ознакомиться с математической моделью затвердевания и охлаждения слябов при НРС,
  
• 
  определить коэффициенты теплоотдачи по секциям ЗВО, обеспечивающие рациональный температурный режим охлаждения поверхности слитка;
  
• 
  определить расходы воды на секции ЗВО и общий расход воды на МНЛЗ;
  
• 
  определить динамику и время затвердевания, глубину жидкой фазы.
  

1. 
   Математическая модель затвердевания и охлаждения слябового слитка при непрерывной разливке стали
   

1. 
   Описание процесса затвердевания и охлаждения слябов на МНЛЗ
   

На рис. 1 показана схема технологической линии по формированию слябового слитка на вертикальной машине непрерывного литья заготовок (МНЛЗ).



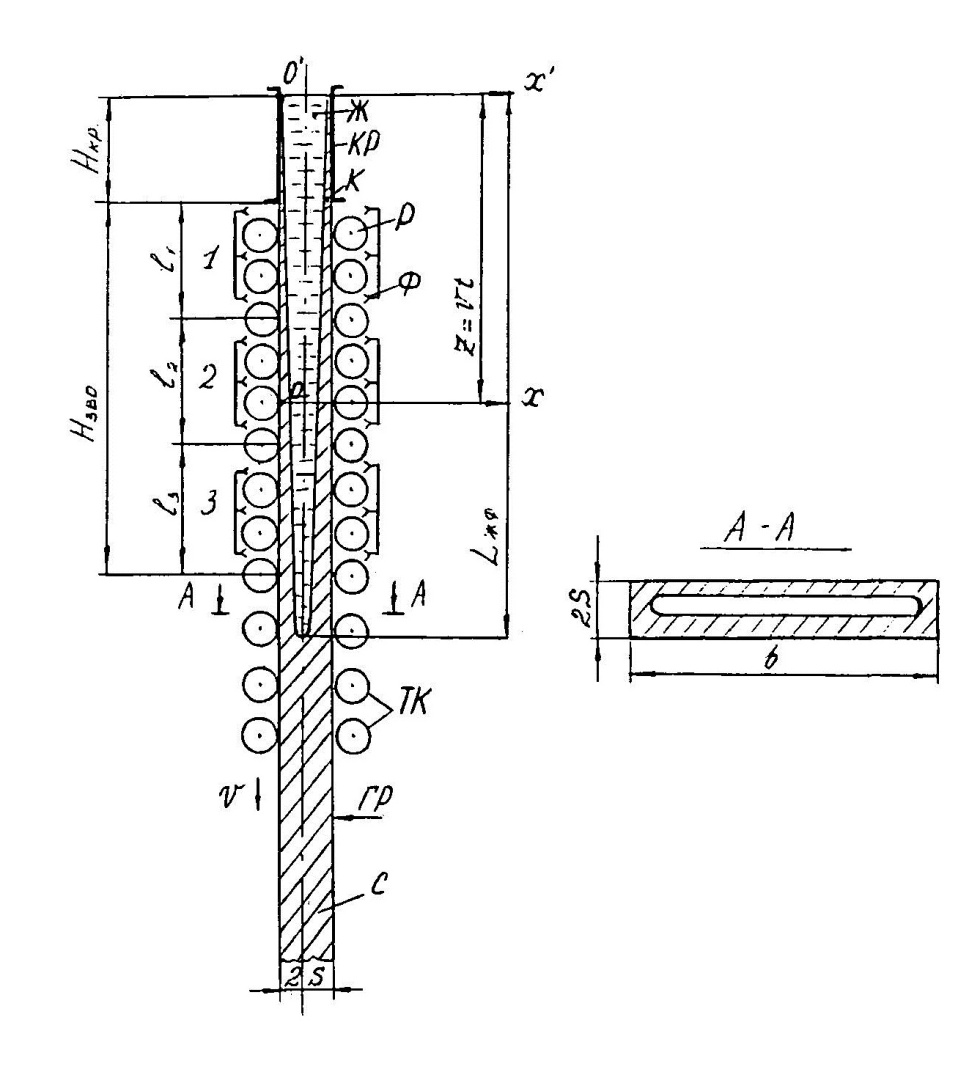
Рис. 1. Схема затвердевания и охлаждения слитка при непрерывной разливке стали на вертикальной МНЛЗ: с – слиток, к – корка, ж – жидкая стали, КР –кристаллизатор, ТК – тянущая клеть, Р – поддерживающие ролики, ГР – газорезка, Нкр – рабочая длина кристаллизатора, Нзво – длина

---

зоны вторичного охлаждения, l1-l3 – длины секций ЗВО, Lжф – глубина жидкой фазы, 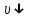- направление скорости втягивания слитка, Ф – форсунки, ОХ’ и ОХ’ – начальное и промежуточное положение расчетного сечения в подвижной системе координат, 2S – толщина.

Слиток (с) условно разделен плоскостью, проходящей через середины широких граней. Жидкая сталь непрерывно поступает из промежуточного ковша через разливочный стакан в кристаллизатор (КР), в котором формируется наружная твердая оболочка (корка - К) слитка за счет отвода тепла в кристаллизатор и кристаллизации металла на рабочей поверхности кристаллизатора. Слиток в виде твердой оболочки (К) с жидким расплавом (Ж) внутри вытягивается из кристаллизатора и попадает в роликовую проводку, которая помогает оболочке сохранить прямоугольную при действии ферростатического давления форму. Проводка конструктивно выполнена из роликовых секций (1-3), поддерживающих широкие грани оболочки слитка. Роликовые секции, как правило, конструктивно по длине совпадают с секциями (1-3) зоны вторичного охлаждения, в которых поверхность слитка охлаждается с помощью водяных или водовоздушных форсунок. Длина проводки определяется глубиной жидкой фазы, а длина зоны вторичного охлаждения - предельным значением коэффициента теплоотдачи, выбираемым из условия плавного перехода кривой охлаждения поверхности слитка при переходе от принудительного охлаждения к естественному (путем свободной конвекции воздуха и излучением). В тянущую клеть (ТК) сечение слитка попадает полностью затвердевшим. После тянущей клети располагается участок газокислородной резки, где слиток разрезается на мерные “длины”.

При разработке математической модели процесса затвердевания и охлаждения слябового слитка приняты следующие физические допущения:

1. 
   Процесс затвердевания слябового слитка можно считать одномерным и рассматривать только в плоскости, проходящей через середины широких граней.
   
2. 
   Процесс затвердевания при постоянной скорости литья – стационарный.
   
3. 
   Процессом молекулярной теплопроводности вдоль слитка можно пренебречь.
   
4. 
   Охлаждение слитка в кристаллизаторе происходит по закону Ньютона с заданным коэффициентом теплоотдачи.
   
5. 
   Охлаждение слитка в секциях ЗВО происходит по закону Ньютона с зависящим от расхода воды коэффициентом теплоотдачи.
   
6. 
   Охлаждение слитка на воздухе после ЗВО имитируется законом Ньютона со средним значением коэффициента теплоотдачи.
   
7. 
   Кристаллизация металла происходит с равномерным теплом в интервале температур ликвидуса и солидуса, соответствующих содержанию углерода и диаграмме Fe-С.
   

---

С учетом этих допущений вместо стационарного процесса затвердевания металла в указанном сечении достаточно рассмотреть затвердевание расчетного (контрольного) сечения, перемещающегося вдоль слитка от мениска до газорезки с постоянной скоростью литья (рис. 2).



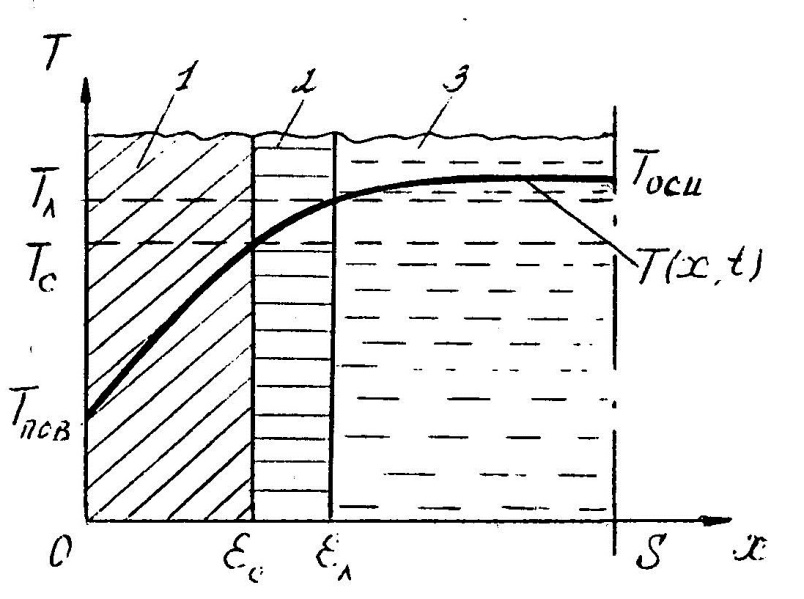
Рис. 2. Расчетное сечение слитка: 1 - твердая фаза (корка), 2 - двухфазная зона, 3 - жидкая фаза, Т (х, t) - распределение температуры.

Расположение сечения на технологической линии определяется координатой 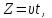где t - текущее время затвердевания металла в рассматриваемом сечении.

2. 
   Математическое описание процесса затвердевания и охлаждения сляба на МНЛЗ.
   

Математическое описание процесса затвердевания и охлаждения слитка включает одномерное уравнение теплопроводности, общее для жидкой, твердожидкой (двухфазной) и твердой зон, и учитывающее выделение тепла кристаллизации в интервале температур ликвидуса и солидуса:

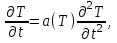(1)

где ,

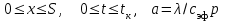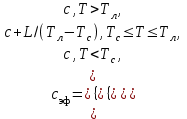(2)

граничные условия типа Ньютона на охлаждаемой поверхности:

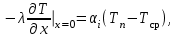(3)

граничные условия в плоскости симметрии:

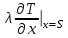(4)

и начальное условие:

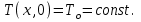(5)

Здесь: S - половина толщины слитка, t - время, х - координата по толщине слитка, отсчитываемая от поверхности слитка в сторону плоскости симметрии (рис. П.1.2), 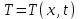- распределение температуры по толщине слитка в момент времени t, а - температуропроводность, - теплопроводность, 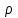- плотность, с - теплоемкость твердой и жидкой фаз, L

---

Смотрите также файлы

• Почему возникают конфликты.docx

• Мені сйікті кейіпкерім Марк Твенні шыармаларыны ішінде маан ерекше наан шыарма Том Сойерді бастан кешкен оиалары.docx

• Итого по авансовому отчету (расход) 8 28 742,00 Расходный кассовый ордер 34 Выдано коммерческому директору.pdf

• Бытие объективной реальности. Материальность мира.ppt

• Возможность и действительность.ppt