ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 54
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; S- половина толщины пластины
Рис.2. Схема расчетной области и распределения температуры по толщине пластины.
Зададим начальное и граничные условия для решения уравнения (1) :
T(0,х)=Т0, (2)
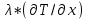= 0 (3)
3) граничное условие III рода на охлаждаемой поверхности при x=S:
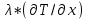- = α (Tпов-Тср) (4)
α – коэффициент теплоотдачи, Тср- температура воды.
Граничное условие при x= S при охлаждении тела излучением имеет вид:
(5)
где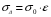
, σ0 - коэффициент излучения абсолютно черного тела.
, 
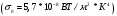- степень черноты поверхности пластины.
Численная модель представляет собой алгоритм решения системы уравнений (1) - (5), полученный с использованием численного метода – метода конечных разностей (МКР). В этом методе непрерывное течение времени заменяют дискретным с шагом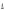
t. Непрерывное изменение координат заменяется дискретными значениями, и вместо непрерывных функций рассматриваются дискретные или сеточные функции. Для этого расчетная область 0
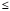х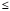 s делится на выбранное количество узлов N и определяется:
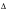x=S/N,
где N – количество внедренных узлов в расчетной области,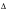 x – шаг по координате х.
Схема пространственной дискретизации области приведена на рис.3.
i= 1, … N внутренние узлы (00), i= 0, i= N +1 – фиктивные узлы (хх).
Рис. 3 Схема дискретизации расчетной области 0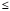
х
s.
Координата узла определяется по формуле:
хi=
x.i – ½ x*= x(i – ½)
Дискретное время:
tn=n* t,
где n – номер временного момента n=0,1,2…., [tk/ t].
На рис. 4 представлена схема пространственной и временной дискретизации области.
Рис.4 Дискредитация расчетной области: t – шаг по времени; n, (n+1) – временные слои, о – внутренние узлы; х – фиктивные узлы, i – номер узла.
? – шаблон расчета температуры в узле хi в n+1момент времени по формуле (8).
Запишем приближенное значение для частной производной по времени:
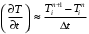(6).
Для замены производного второго порядка по координате используем дополнительные промежуточные узлы на рис.5 i+½, i -½.
Рис.5 Схема к аппроксимации производной второго порядка.
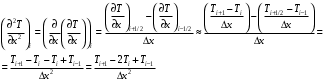(7).
Подставляем (6) и (7) в уравнение теплопроводности (1), получим его конечно-разностный аналог, из которого выразим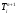
:
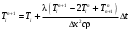, i=1…N (8).
Распределение температуры по узлам в начальный момент времени в конечно-разностном виде. Граничное условие в конечно-разностном виде:
При х =0,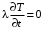
, 
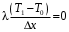или T0=T1.
Граничное условие при x=S:
.
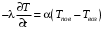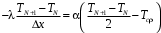
Выразим TN+1 из последнего уравнения:
,
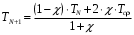где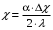
.
Основу алгоритма составляет формула (8), которая выполняется в цикле по i и n. Алгоритм численного решения реализован на языке ПАСКАЛЬ-7 (программа
pas – для охлаждения конвекцией и программа П5.pas – путем измерения).
Подготовка исходных данных для программ.
В таблице 1 приведены варианты заданий. Номер варианта соответствует номеру фамилии студента в списке у преподавателя.
Таблица 1 – Варианты заданий для исследования охлаждения пластины.
Исходные данные, соответствующие заданию студента, заносятся в общие исходные данные (табл.2) используемые в программе.
Таблица 2 – исходные данные к программе расчета процесса охлаждения пластины конвекцией (или путем излучения)
В случае подготовки исходных данных к программе расчета процесса охлаждения пластины путем излучения в строке 7 в табл.2 заносится степень черноты (ε). В первую очередь в таблице №2 заносятся S, Т0, α или ε. Конечное время процесса tк подбирается так, чтобы температура оси тела снизилась за время процесса до значения менее 100 оС. Шаг выдачи ∆p задается так, чтобы количество выдач было не менее 10 за время процесса. При заполнении табл.2 обратить внимание на размерность физических величин.
Сначала моделирование проводится для среднего значения варьируемого параметра.После подбора tkи ∆p результаты расчета температуры по толщине пластины для всех выдач результатов заносят в табл.3 и 4.
В табл.3 для каждой выдачи записывают Тоси (х=о), Т (х=0,5 *S), Тnoв (x=S) . В табл.4 записывают номера узлов (1,3,5,7,9,11), координаты этих узлов и значения температуры в указанных точках(узлах 1,3,5,7,9,11) для трех моментов времени 0,1/8tk,1/4 tk, 1/2 tk и tk сек, близких к моментам выдачи результатов, где tk – конечное время процесса.
Рис.2. Схема расчетной области и распределения температуры по толщине пластины.
Зададим начальное и граничные условия для решения уравнения (1) :
-
начальное условие в момент времени t =0:
T(0,х)=Т0, (2)
-
граничное условие на оси пластины при х=0 (условие симметрии):
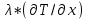= 0 (3)3) граничное условие III рода на охлаждаемой поверхности при x=S:
-
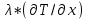= α (Tпов-Тср) (4)α – коэффициент теплоотдачи, Тср- температура воды.
Граничное условие при x= S при охлаждении тела излучением имеет вид:
(5)где
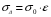, σ0 - коэффициент излучения абсолютно черного тела. 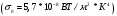, - степень черноты поверхности пластины.-
Численная модель процесса охлаждения.
Численная модель представляет собой алгоритм решения системы уравнений (1) - (5), полученный с использованием численного метода – метода конечных разностей (МКР). В этом методе непрерывное течение времени заменяют дискретным с шагом
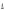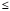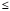t. Непрерывное изменение координат заменяется дискретными значениями, и вместо непрерывных функций рассматриваются дискретные или сеточные функции. Для этого расчетная область 0 х s делится на выбранное количество узлов N и определяется: 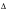x=S/N,где N – количество внедренных узлов в расчетной области,
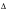x – шаг по координате х.Схема пространственной дискретизации области приведена на рис.3.
i= 1, … N внутренние узлы (00), i= 0, i= N +1 – фиктивные узлы (хх).
Рис. 3 Схема дискретизации расчетной области 0
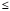
х
s.Координата узла определяется по формуле:
хi=
x.i – ½ x*= x(i – ½)Дискретное время:
tn=n*
t,где n – номер временного момента n=0,1,2…., [tk/
t].На рис. 4 представлена схема пространственной и временной дискретизации области.
Рис.4 Дискредитация расчетной области:
t – шаг по времени; n, (n+1) – временные слои, о – внутренние узлы; х – фиктивные узлы, i – номер узла. ? – шаблон расчета температуры в узле хi в n+1момент времени по формуле (8).
Запишем приближенное значение для частной производной по времени:
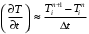(6).Для замены производного второго порядка по координате используем дополнительные промежуточные узлы на рис.5 i+½, i -½.
Рис.5 Схема к аппроксимации производной второго порядка.
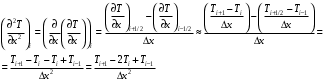(7).Подставляем (6) и (7) в уравнение теплопроводности (1), получим его конечно-разностный аналог, из которого выразим
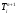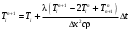: , i=1…N (8).Распределение температуры по узлам в начальный момент времени в конечно-разностном виде. Граничное условие в конечно-разностном виде:
При х =0,
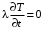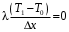, или T0=T1.Граничное условие при x=S:
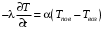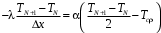
. Выразим TN+1 из последнего уравнения:
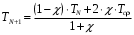,где
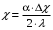.Основу алгоритма составляет формула (8), которая выполняется в цикле по i и n. Алгоритм численного решения реализован на языке ПАСКАЛЬ-7 (программа
pas – для охлаждения конвекцией и программа П5.pas – путем измерения).
Подготовка исходных данных для программ.
В таблице 1 приведены варианты заданий. Номер варианта соответствует номеру фамилии студента в списке у преподавателя.
Таблица 1 – Варианты заданий для исследования охлаждения пластины.
| Охлаждение конвекцией | |||
| № варианта | S- половина толщины, м | Тb- начальная температура,оС | α – коэффициент теплоотдачи, Вт/м2к |
| 1 | 2 | 3 | 4 |
| 1 | 0.05; 0,1; 0.2 | 1000 | 250 |
| 2 | --«-- | --«-- | 500 |
| 3 | --«-- | --«-- | 1000 |
| 4 | 0.05 | --«-- | 250,500,1000 |
| 5 | 0.1 | --«-- | --«-- |
| 6 | 0.2 | --«-- | --«-- |
| 7 | 0.1 | 500,1000,1500 | 250 |
| 8 | 0.1 | --«-- | 500 |
| 9 | 0.1 | --«-- | 1000 |
| Охлаждение путем излучения | |||
| № варианта | Sм | То ;К | ε- степень черноты поверхности |
| 10 | 0.05; 0.1; 0.2 | 500 | 0.8 |
| 11 | --«-- | 1000 | --«-- |
| 12 | --«-- | 1500 | --«-- |
| 13 | 0.05 | 500;1000;1500 | --«-- |
| 14 | 0.1 | --«-- | --«-- |
| 15 | 0.2 | --«-- | --«-- |
| 16 | 0.1 | 500 | 0.6;0.8;1.0 |
| 17 | 0.1 | 1000 | --«-- |
| 18 | 0.1 | 1500 | --«-- |
Исходные данные, соответствующие заданию студента, заносятся в общие исходные данные (табл.2) используемые в программе.
Таблица 2 – исходные данные к программе расчета процесса охлаждения пластины конвекцией (или путем излучения)
| № п/п | Обозначения | Идентификатор | Название величины | Размерность | Значение |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | То | TO | Начальная температура станины | 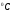 /K | 1000 |
| 2 | ρ | P | Плотность стали | кг/м3 | 7500 |
| 3 | c | C | Теплоемкость стали | Дж/кг*K | 700 |
| 4 | S | S | Половина толщины пластины | м | 0.1 |
| 5 |  | Lam | Коэффициент теплопроводности стали | Вт/м*K | 30 |
| 6 | Тср | Tsr | Температура среды | 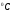/K | 7 |
| 7 | α/ε | Alfa/eps | Коэффициент теплоотдачи/степень черноты) | Вт/м2*K/- | 500/0,8 |
| 8 | N | N | Количество внутренних узлов по толщине | -- | 11 |
| 9 | ∆p | dp | Шаг выдачи результатов | cек | 60 |
| 10 | tk | tk | Конечное время процесса | cек | 3600 |
| 11 | ky | Ky | Коэффициент устойчивости | -- | 3.0 |
В случае подготовки исходных данных к программе расчета процесса охлаждения пластины путем излучения в строке 7 в табл.2 заносится степень черноты (ε). В первую очередь в таблице №2 заносятся S, Т0, α или ε. Конечное время процесса tк подбирается так, чтобы температура оси тела снизилась за время процесса до значения менее 100 оС. Шаг выдачи ∆p задается так, чтобы количество выдач было не менее 10 за время процесса. При заполнении табл.2 обратить внимание на размерность физических величин.
Сначала моделирование проводится для среднего значения варьируемого параметра.После подбора tkи ∆p результаты расчета температуры по толщине пластины для всех выдач результатов заносят в табл.3 и 4.
В табл.3 для каждой выдачи записывают Тоси (х=о), Т (х=0,5 *S), Тnoв (x=S) . В табл.4 записывают номера узлов (1,3,5,7,9,11), координаты этих узлов и значения температуры в указанных точках(узлах 1,3,5,7,9,11) для трех моментов времени 0,1/8tk,1/4 tk, 1/2 tk и tk сек, близких к моментам выдачи результатов, где tk – конечное время процесса.