При занесении значений температуры во внутренних узлах особое внимание обратить на номер узла и его соответствие координате х по толщине сляба. Последнее особенно важно при построении распределения температуры (рис. 2.6) по толщине сляба.

Таблица 2.7
Результаты моделирования рационального режима нагрева сляба

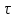, сек	h, м		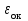Тпв	Тпн	Тпв	Тпн	Т1	Т2	Т3	Т4	Т5
0	0	0	1250	1280	20	20	20	20	20	20	20
1000	3	0,00	1250	1280	542	578	465	369	342	381	490
2000	6	0,01	1250	1280	843	872	751	654	626	665	772
3000	9	0,05	1250	1280	974	1003	901	800	771	813	925
4000	12	0,13	1250	1280	1058	1084	1004	928	904	940	1026
5000	15	0,23	1250	1280	1124	1147	1087	1037	1022	1047	1107
6000	18	0,39	1300	1280	1220	1195	1187	1138	1119	1130	1168
7000	21	0,55	1300	1280	1256	1229	1235	1202	1187	1191	1213
8000	24	0,71	1300	1280	1279	1238	1265	1244	1232	1232	1237
9000	27	0,83	1290	1280	1246	1240	1247	1248	1245	1242	1244
10000	30	0,92	1290	1280	1242	1243	1242	1247	1243	1243	1243

---

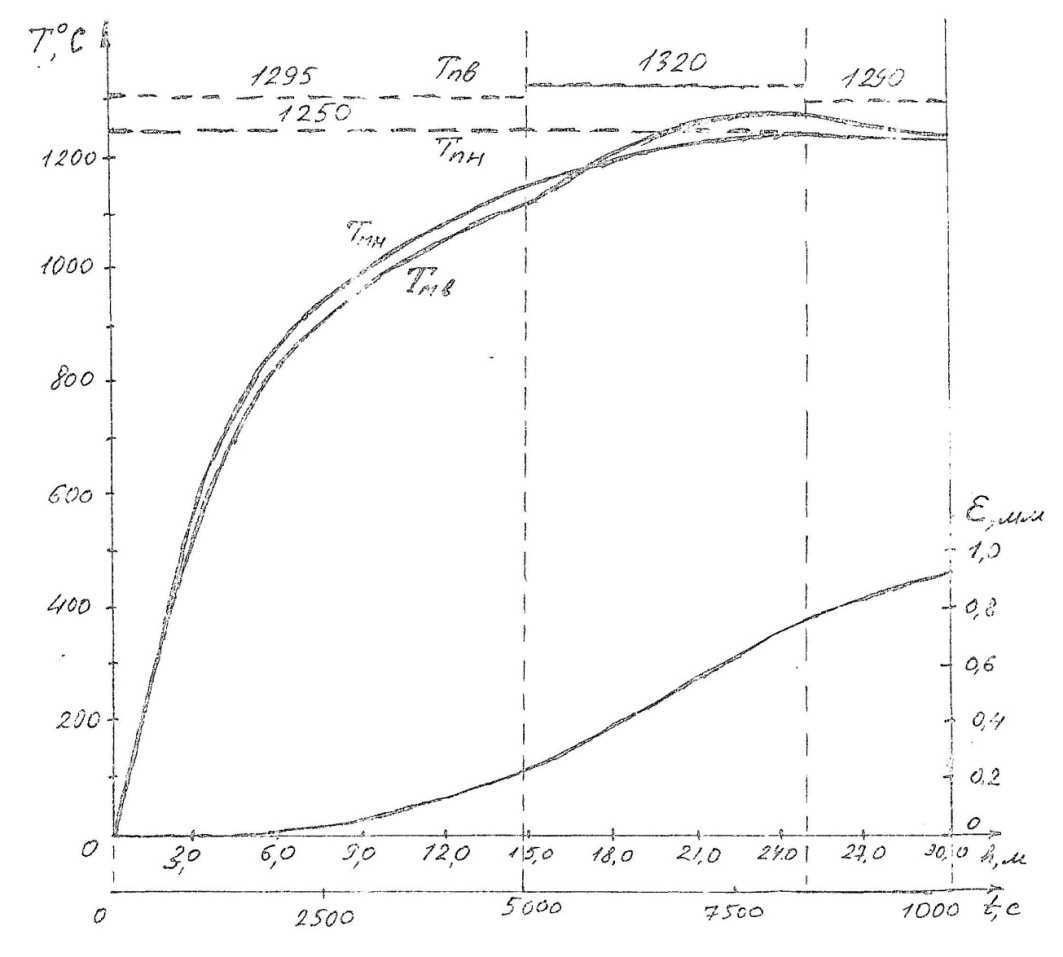
Рис. 2.5. Кривые нагрева верхней (Т_мв) и нижней (Т_мн) поверхностей сляба, толщины окалины (h_ок) и режим нагрева сляба сверху (Т_пв) и снизу (Т_пк) в различных зонах печи.
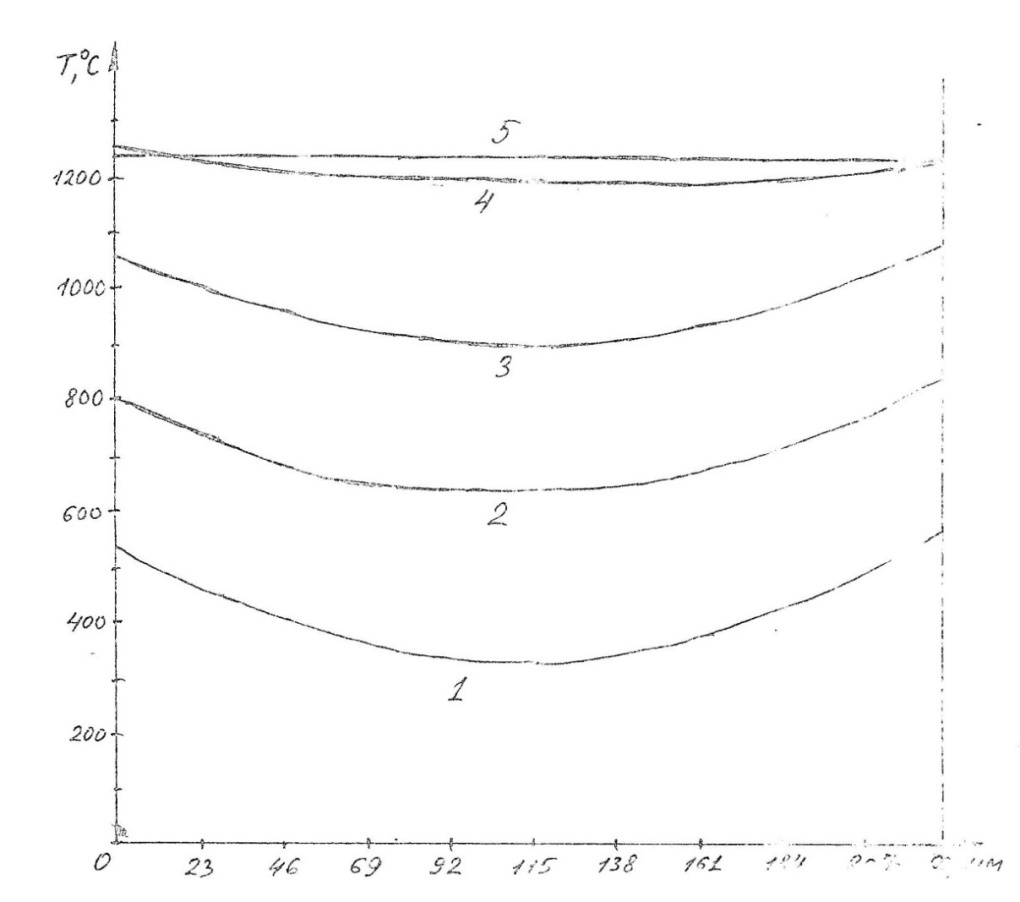
Рис. 2.6. Распределение температуры по толщине сляба для нескольких моментов времени: 1-1000 с, 2-2000, 3-4000, 4-7000, 5-10000 с.

2. 
   Порядок выполнения работы
   

1. 
   Ознакомиться с целью работы, задачами моделирования, компьютерной моделью.
   
2. 
   Подготовить исходные данные к программе согласно варианта моделирования.
   
3. 
   Заполнить таблицу вариантов исходных данных и массивов.
   
4. 
   Провести моделирование при первом варианте исходных данных с контролем соответствия выдаваемых на печать температуры среды сверху и снизу сляба в зоне расположения сляба в печи. Проанализировать процесс нагрева и результаты моделирования в последней печати с точки зрения рациональности назначенного режима нагрева.
   
5. 
   Скорректировать режим нагрева согласно указаний в п.1 и повторять моделирование с целью найти рациональный режим нагрева (табл.2.6)
   
6. 
   После определения самого рационального режима нагрева заполнить таблицу результатов (табл. 2.7).
   
7. 
   Построить графики температуры среды по зонам, температуры поверхности верхней и нижней, толщины окалины во времени, а также распределения температуры по толщине сляба согласно приведенным примерам.
   
8. 
   В выводах указать рациональный режим нагрева в виде температуры среды по зонам, температуру металла, максимальный перепад температур и толщину окалины при выдаче сляба из печи.
   

3. 
   Содержание отчета
   

1. 
   Номер задания, цели и задачи моделирования.
   
2. 
   Таблица задания варианта моделирования (в форме табл. 2.3).
   
3. 
   Расчет исходных данных.
   
4. 
   Таблица вариантов и массивов с указанием всех смоделированных режимов нагрева и обоснованием выбора нового режима, и, в частности, последнего - рационального.
   
5. 
   Таблица результатов нагрева металла при рациональном режиме.
   
6. 
   Рисунок с графиками рациональных режимов нагрева, динамики температуры и окалины по длине печи.
   
7. 
   Рисунок с распределением температуры по толщине сляба для пяти моментов времени.
   
8. 
   Выводы о рациональном режиме нагрева, температуре металла, перепаде температуры и толщине окалины.
   

---

4. 
   Контрольные вопросы
   

1. 
   Что такое режим нагрева металла в печи?
   
2. 
   Дать определение рационального режима нагрева.
   
3. 
   В каких зонах и как корректируется режим нагрева при превышении (значений) температура поверхности сляба на выходе из печи по сравнению с допустимой?
   
4. 
   Как регулируется режим нагрева при превышении конечным перепадам температуры допустимого значения?
   

5. 
   Литература
   

1. 
   Прудковский Б.А. Зачем металлургу математические модели? - М.: Наука, 1989. 192 с.
   
2. 
   Металлургическая теплотехника. В 2-х томах. Т.1. Теоретические основы: Учебник для вузов / Кривандин В.А., Арутюнов В.А., Мастрюков В.С. и др. – Металлургия, 1986. 424 с.
   
3. 
   Технология математического моделирования металлургических процессов: курс лекций: учебное пособие для вузов / З. К. Кабаков, М. А. Пахолкова; Кабаков З.К., Пахолкова М.А. - Череповец: ФГБОУ ВПО ЧГУ, 2012. - 132 с. + Приложения. - Библиогр.: с.109-112.
   

---

Лабораторная работа №2 Нагрев и охлаждение тел простой формы

Цель работы: Изучить влияние интенсивности охлаждения (нагрева) тел простой формы на время их охлаждения (нагрева) при конвективном и лучистом теплообмене

Задача работы:

- исследовать распределение температуры по толщине (радиусу) тела для среднего значения варьируемого параметра;

- исследовать динамику охлаждения оси и поверхности тела во времени для среднего значения варьируемого параметра;

- определить продолжительность охлаждения тела для 3-х значений варьируемого параметра до температуры оси, равной заданному значению.

1. Сведения об объекте исследования
Объектом исследования является стальная пластина, охлаждаемая водой, или путем измерения. Схема объекта приведена на рис.1.

---

1. 
   - пластина,2- охлаждение водой, 3- опоры.
   

Рис.1. Схема охлаждения стальной пластины.
Относительно объекта приняты следующиеупрощающие допущения:

1. 
   теплофизические свойства стали в процессе охлаждения не изменяются;
   
2. 
   условия охлаждения симметричны;
   
3. 
   охлаждение идёт от равномерной начальной температуры;
   
4. 
   температура среды постоянна;
   
5. 
   а/b> 3, l/b>3,где b = 2*S – толщина пластины,a-ширина,l–длина.
   
1. 
   Математическая модель охлаждения пластины
   

При принятых допущениях модель включает одномерное нестационарное уравнение теплопроводности:

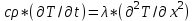, 0 ≤ х ≤ S, 0 ≤t ≤ t_{к , (1)}

где:Т – температура;t – время;S – половина тощины пластины,

с - теплоёмкость материала, Дж/(кг*К); ρ- плотность, кг/м³;

λ – коэффициент теплопроводности, Вт/(м*К);t_к – конечное время.

Расчетная область для уравнения (1) приведена на рис.2.
Т(x,t)












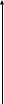
Tп





х

0 S
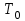- начальная температура; - температура поверхности

---

Смотрите также файлы

• Почему возникают конфликты.docx

• Мені сйікті кейіпкерім Марк Твенні шыармаларыны ішінде маан ерекше наан шыарма Том Сойерді бастан кешкен оиалары.docx

• Итого по авансовому отчету (расход) 8 28 742,00 Расходный кассовый ордер 34 Выдано коммерческому директору.pdf

• Бытие объективной реальности. Материальность мира.ppt

• Возможность и действительность.ppt