ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 198
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать, используя исходное соотношение:
Чтобы получить общую сумму сделок, необходимо по каждой сделке курс продажи (Хi) умножить на количество проданных акций (fi) и полученные произведения сложить:
Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной:
(15)В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Если для расчета средней по данным табл. 19 использовать удельные веса, преобразовав формулу (15), получим:
(16)Или можно выразить удельный вес в долях единицы:
При расчете средней по интервальному вариационному ряду от интервалов переходят к их серединам. При этом ширина открытых интервалов (первого и последнего) условно приравнивается к ширине интервалов, примыкающих к ним (второго и предпоследнего). Рассмотрим следующий пример (табл. 20).
Таблица 20.
Распределение сотрудников предприятия по возрасту
| Возраст (лет) | Число сотрудников (чел.) |
| до 25 | 8 |
| 25–30 | 32 |
| 30–40 | 68 |
| 40–50 | 49 |
| 50–60 | 21 |
| 60 и более | 3 |
| Итого: | 181 |
Для определения среднего возраста персонала найдем середины возрастных интервалов: 22,5 (для интервала до 25), 27,5 (для интервала 25–30), 35,0 (для интервала 30–40), 45,0 (для интервала 40–50), 55,0 (для интервала 50–60), 65,0 (для интервала 60 и более).
Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия:
На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов. Например, имеются следующие данные:
Таблица 21.
Себестоимость продукции «Z»
| Предприятие | Себестоимость единицы продукции, руб. |
| 1. | 37 |
| 2. | 39 |
Можно ли по имеющимся данным определить среднюю себестоимость единицы продукции по двум предприятиям вместе? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. ((37 + 39) : 2). Однако если на первом предприятии произведено 50 единиц продукции, а на втором – 700, для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная:
Вывод: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.
Средняя арифметическая обладает математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев используются для ее расчета. Рассмотрим эти свойства.
1.Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
(17)Проверим свойство на примере расчета среднего курса продажи акций (табл. 19). За счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться:
417,03 ´ 1 850 = 420 ´ 700 + 440 ´ 200 + 410 ´ 950
2.Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:
(18)Для нашего примера:
(420 – 417,03) ´ 700 + (440 – 417,03) ´ 200 + (410 – 417,03) ´ 950 0
3.Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С.
Рассмотрим это свойство на упрощенном примере по ряду данных xi = 3, 4, 5. Средняя величина для данного ряда равна 4. Рассчитаем сумму квадратов отклонений от = 4 и от величины С, приняв ее за вариант xi = 3:
| | |  | | | | ( )2 |
| 3 | 3 – 4 = -1 | (-1)2= 1 | | 3 | 3 – 3 = 0 | (0) 2= 0 |
| 4 | 4 – 4 = 0 | 02 = 0 | | 4 | 4 – 3 = 1 | 1 2 = 1 |
| 5 | 5 – 4 = 1 | 12 = 1 | | 5 | 5 – 3 = 2 | 22 = 4 |
| | | | | | | |
| Итого | - | 2 | | Итого | 0 | 5 |
Каким бы большим или малым мы ни брали число С, сумма квадратов отклонений индивидуальных значений признака от нее всегда будет больше суммы квадратов их отклонений от средней на величину:
(19)4.Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину А:
(20)Так, если все курсы продажи акций увеличить на 15 руб., то средний курс также увеличится на 15 руб.:
5.Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:
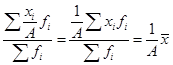(21)Предположим, курс продажи в каждом случае вырос в 2 раза. Тогда и средний курс также увеличится на 100 %:
6.Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
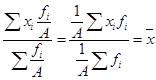(22)Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100:
Вопрос 3. Средняя гармоническая, квадратическая и геометрическая.
Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Другими словами, когда в исходных данных нам известны индивидуальные усредняемые значения хi, но нет прямой информации о количестве объектов, т.е. о частотах fi, однако эти данные можно получить при помощи простых расчетов. Например, известна цена 1 кг товара – 50 руб. и общий объем его реализации – 250 руб. Прямого указания на количество реализованных килограмм товара нет, но, разделив 250 на 50, мы легко узнаем, что всего было продано 5 кг. Рассмотрим расчет средней гармонической взвешенной на примере данных таблицы 22.
Таблица 22.
Реализация товара на трех рынках города за II квартал 2012 г.
| Рынок | Цена товара за 1 кг, руб. xi | Выручка от реализации, тыс. руб., Wi = xi * fi |
| А | 95 | 1900 |
| Б | 80 | 2800 |
| В | 90 | 2070 |
Средняя цена любого товара может быть определена только на основе следующего исходного соотношения:
Общую выручку легко получить простым суммированием выручек по трем рынкам. Данные же о количестве реализованного товара в кг отсутствуют, но их можно узнать, разделив размер выручки от реализации каждого рынка на цену товара. Определим искомую среднюю:
Таким образом, всего было реализовано 78 кг товара, а средняя цена реализации за II квартал 2012 г. составила 86 руб. 79 коп. за 1 кг. В данном случае расчет произведен по формуле средней гармонической взвешенной (23) , где Wi – выручка от реализации, представляющая собой произведение цены товара (хi, руб.) на объем его реализации (fi, кг.)
, (23)где
.Средняя геометрическая рассчитывается по формулам:
– невзвешенная (24)
– взвешенная (25)Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей теме.
Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:
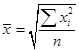– невзвешенная (26)
– взвешенная (27)Данный вид средней используется при расчете показателей вариации.
Вопрос 4. Средняя хронологическая.
Средний уровень моментного ряда динамики рассчитывается по формулесредней хронологической. Для моментного равноотстоящего ряда динамики при расчете среднего уровня используют формулу средней хронологической простой:
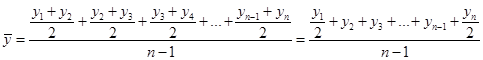(28)или
Например, требуется найти среднесписочную месячную численность работников предприятия по данным об их численности на 1-е число каждого месяца в первом квартале 2013 г. (чел.):
| 1/I | 1/II | 1/III | 1/IV |
| 347 | 350 | 349 | 351 |