Номер	x	y	x^2	y^2	x*y	y(x)
1	2,5	69	6,25	4761	172,5	66,62372288
2	3	65	9	4225	195	64,92288314
3	3,4	63	11,56	3969	214,2	63,56221134
4	4,1	59	16,81	3481	241,9	61,18103569
5	5	57	25	3249	285	58,11952414
6	6,3	55	39,69	3025	346,5	53,6973408
7	7	54	49	2916	378	51,31616515
8	4,7	58	22,09	3364	272,6	59,14002799
9	3,9	64	15,21	4096	249,6	61,86137159
10	4,2	60	17,64	3600	252	60,84086774
11	5,8	53	33,64	2809	307,4	55,39818055
12	6,7	52	44,89	2704	348,4	52,336669
Сумма	56,6	709	290,78	42199	3263,1	709
Среднее	4,716666667	59,08333333	24,23166667	3516,583333	271,925	59,08333333

---

Выборочные средние.



Выборочные дисперсии:



коэффициент линейной парной корреляции:


Спецификация:

На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a

Система нормальных уравнений.
an + b∑x = ∑y
a∑x + b∑x² = ∑yx

12a + 56.6·b = 709
56.6·a + 290.78·b = 3263.1
Домножим уравнение (1) системы на (-4.717), получим систему, которую решим методом алгебраического сложения.
-56.6a -266.982 b = -3344.353
56.6*a + 290.78*b = 3263.1
Получаем:
23.798*b = -81.253
Откуда b = -3.4017
Теперь найдем коэффициент «a» из уравнения (1):
12a + 56.6*b = 709
12a + 56.6*(-3.4017) = 709
12a = 901.535
a = 75.1279
Получаем эмпирические коэффициенты регрессии: b = -3.4017, a = 75.1279
Уравнение регрессии:
y = -3.4017x + 75.1279

1. 
   Критерий Дарбина-Уотсона. Проверка на коррелированность значений случайной компоненты (критерий дарбина-уотсона).
   

y	y(x)	ei = y-y(x)	e2	(ei - ei-1)2
69	66.624	2.376	5.647	0
65	64.923	0.0771	0.00595	5.286
63	63.562	-0.562	0.316	0.409
59	61.181	-2.181	4.757	2.621
57	58.12	-1.12	1.253	1.127
55	53.697	1.303	1.697	5.867
54	51.316	2.684	7.203	1.908
58	59.14	-1.14	1.3	14.622
64	61.861	2.139	4.574	10.75
60	60.841	-0.841	0.707	8.877
53	55.398	-2.398	5.751	2.425
52	52.337	-0.337	0.113	4.25
			33.324	58.141

---

d₁ < DW и d₂ < DW < 4 - d₂. Поскольку 1.08 < 1.74 и 1.36 < 1.74 < 4 - 1.36, то автокорреляция остатков отсутствует.

Проверка нормальности распределения остаточной компоненты.
Расчетное значение RS-критерия равно:

где ε_max = 2.6838 – максимальное значение остатков, ε_min = -2.3982 – минимальный уровень ряда остатков.
S_ε – среднеквадратическое отклонение
Несмещенная оценка среднеквадратического отклонения.


Расчетное значение RS-критерия попадает в интервал (2,7-3,7), следовательно, выполняется свойство нормального распределения.

Тест Голдфелда-Квандта.

Упорядочим все значения по величине X.
Находим размер подвыборки k = (12 - 3)/2 = 5.
где c = 4n/15 = 4*12/15 = 3
Оценим регрессию для первой подвыборки.

Система уравнений МНК:
a₀n + a₁∑x = ∑y
a₀∑x + a₁∑x² = ∑y•x
Для наших данных система уравнений имеет вид:
5a₀ + 16.9a₁ = 320
16.9a₀ + 58.83a₁ = 1073.2
Из первого уравнения выражаем а₀ и подставим во второе уравнение
Получаем a₀ = -4.92, a₁ = 80.62

x	y	x2	y2	x*y	y(x)	(y-y(x))2
2.5	69	6.25	4761	172.5	68.328	0.452
3	65	9	4225	195	65.869	0.755
3.4	63	11.56	3969	214.2	63.902	0.813
3.9	64	15.21	4096	249.6	61.443	6.54
4.1	59	16.81	3481	241.9	60.459	2.129
16.9	320	58.83	20532	1073.2	320	10.689

---

Здесь S₁ = 10.69
Для последней выборки:

x	y	x2	y2	x*y	y(x)	(y-y(x))2
5	57	25	3249	285	56.09	0.828
5.8	53	33.64	2809	307.4	54.787	3.192
6.3	55	39.69	3025	346.5	53.972	1.057
6.7	52	44.89	2704	348.4	53.32	1.743
7	54	49	2916	378	52.831	1.365
30.8	271	192.22	14703	1665.3	271	8.185

S₃ = 8.19

Число степеней свободы v1 = v2 = (n – c - 2m)/2 = (12 - 3 - 2*1)/2 = 3.5

F = 10.69/8.19 = 1.31
Поскольку F < F_kp = 7.71, то гипотеза об отсутствии гетероскедастичности принимается.

2.

t_крит(n-m-1;α/2) = t_крит(10;0.025) = 2.634


Поскольку 9.09 > 2.634, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

---

Вывод: 40.8 > 2.634, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

3.

F-статистика. Критерий Фишера.






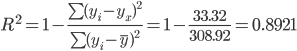
Табличное значение критерия со степенями свободы k₁=1 и k₂=10, F_табл = 4.96

Вывод: фактическое значение F > F_табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).

4.



Вывод: увеличение x на величину среднеквадратического отклонения Sx приведет к уменьшению среднего значения Y на 94.5% среднеквадратичного отклонения Sy.

5.

Последствия автокорреляции случайных возмущений:

- Оценки неизвестных параметров неэффективны (однако остаются несмещенными)

- Расчетные значения дисперсий оценок неизвестных параметров оказываются заниженными, что может привести к признанию статистической значимости незначимых в действительности параметров

- Ухудшаются прогнозные качества модели
Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности:

1. 
   Оценки параметров, оставаясь линейными и несмещенными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок
   
2. 
   Дисперсии оценок являются смещенными. Зачастую дисперсии, вычисляемые по стандартным формулам, являются заниженными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые в действительности таковыми могут и не являться.
   
3. 
   Оценка дисперсии регрессии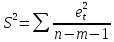   является смещенной оценкой истинного значения  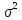, во многих случаях занижая его.
   
4. 
   В силу вышесказанного выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и коэффициента детерминации, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.
   

---

Смотрите также файлы

• Педагогическое общение. Стили педагогического общения.docx

• 1231234.docx

• 1. Источники загрязнения внутренних водоемов 2 Методы очистки сточных вод 7.docx

• Реферат по дисциплине Вирусология и биотехнология Вирус лейкоза крупного рогатого скота.rtf

• Литература по теме Практические задания.docx