Файл: Методические указания для выполнения курсовой работы по дисциплине.doc

На графике привести зависимость и сравнить значение и по величине. Объяснить полученные зависимости.

Примечание. Диапазон нагрузок к УСС (не менее пяти точек) взять из таблицы 4.3 задания 4 так, чтобы .

2.Подобрать такое число линий в направлении к УСС, чтобы с учетом повторных вызовов потери первичных вызовов не превышали заданную норму .

---

Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений: упрощенная формула Эрланга, формула О^’Делла, формула Пальма-Якобеуса

Для практических расчетов пропускной способности однозвенных неполнодоступных включений (рис.8.1) используются приближенные методы.

Упрощенная формула Эрланга:

, (8.1)

где - интенсивность обслуженной пучком линий нагрузки; - вероятность потерь; - доступность; - средняя пропускная способность одной линии пучка. Эта формула дает грубую приближенную оценку пропускной способности неполнодоступного включения (завышается пропускная способность НПД пучка).



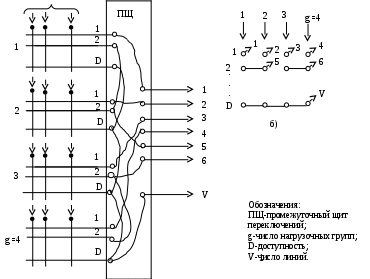
Рис.8.1. Неполнодоступное (НПД) включение линий

а) схема запараллеливания выходов; б) условное изображение НПД схемы.

Формула О’Делла:

, (8.2)

где - нагрузка, обслуженная полнодоступным пучком из линий при потерях и приблизительно определяемая с помощью 1-ой формулы Эрланга (по таблицам Пальма).

Формула Пальма – Якобеуса:

(8.3)

где А – интенсивность поступающей на пучок линий нагрузки.

При малых значениях потерь можно считать . Поэтому все эти формулы при фиксированных

---

и могут быть приведены к виду:

, (8.4)

где значения и зависят от и .

Для упрощенной формулы Эрланга:

, ; (8.5)

Для формулы О’Делла:

, (8.6)
Для формулы Пальма – Якобеуса эти коэффициенты можно подобрать. Значения и для формулы О’Делла табулированы и для некоторых значений и приведены в таблице П.4 Приложения.
Задание 8.
1.Рассчитать и построить зависимости числа линий V и коэффициента среднего использования от интенсивности поступающей нагрузки А при величине потерь , где NN – двухзначный номер варианта, и значениях доступности , используя метод О’Делла. Результаты расчета представить в виде таблицы 8.1 и графика. Значения Асоответствуют нагрузкам на направлениях, рассчитанным при выполнении задания 3 (таблица 3.1). Следить, чтобы выполнялось условие НПД включения V>D.


2. Рассчитать и построить зависимость числа линий от величины потерь

---

неполнодоступного пучка при значении и по формуле Эрланга, О’Делла, Пальма – Якобеуса. Результаты расчета представить в виде таблицы 8.2 и графика.

Таблица 8.1.

Направление связи от АТСЭ-4	А, Эрл
		V		V		V
УСС
АМТС
ЦПС
IP-сеть
АТСЭ – 1
АТСДШ – 2
АТСК – 3
АТСЭ – 4(внутристанционное)

---

Таблица 8.2.

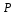
№ п.п.		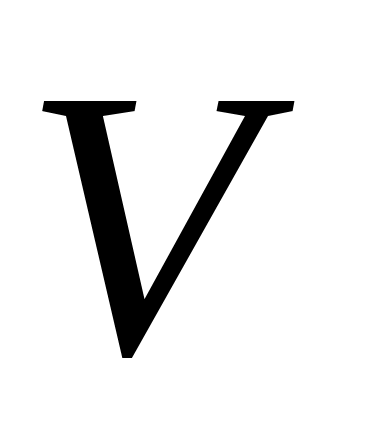, рассчитанное по формулам
		Эрланга	О’ Делла	Пальма –Якобеуса
1 2 3 . . . 10	0,001 0,005 0,01 . . . 0,2

Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений
Многозвенные коммутационные схемы имеют значительно большее число состояний, чем однозвенные. Поэтому система уравнений для вероятностей состояний многозвенной коммутационной схемы не только не может быть решена, но и во многих случаях не может быть записана.

Поэтому для расчета двухзвенных коммутационных схем при полнодоступном включении линий применяется приближенный комбинаторный метод Якобеуса.

Вызов в двухзвенной схеме может быть потерян в одном из трех случаев:

1. 
   если заняты все промежуточные линии, которые могут быть использованы для обслуживания этого вызова;
   
2. 
   если заняты все выходы в требуемом направлении;
   
3. 
   если возникают неудачные комбинации свободных промежуточных линий и свободных выходов.
   

Вид формулы Якобеуса для вероятности потерь в двухзвенной коммутационной схеме при полнодоступном включении линий зависит от соотношения основных коммутационных параметров блока искания,

определяющих применение закона распределения вероятностей занятия обслуживающих устройств на первом и втором звеньях.

Примем следующие обозначения: - число входов в каждый коммутатор звена А; - число выходов из каждого коммутатора звена А;

---