Файл: Методические указания для выполнения курсовой работы по дисциплине.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 180
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- коэффициент сжатия или расширения, 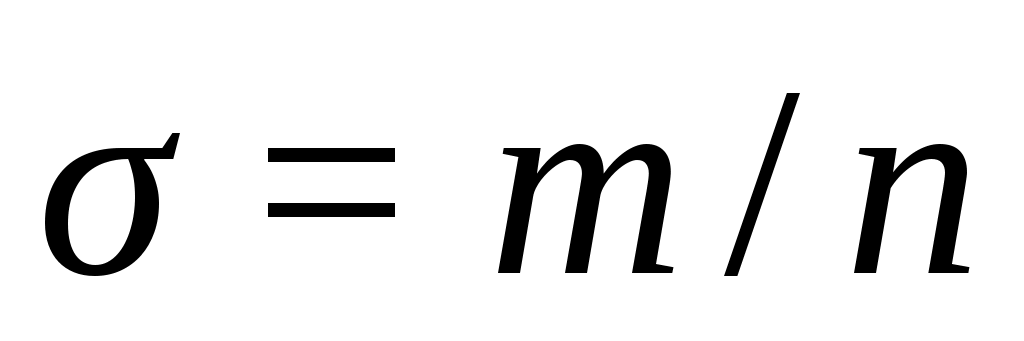 ;
; 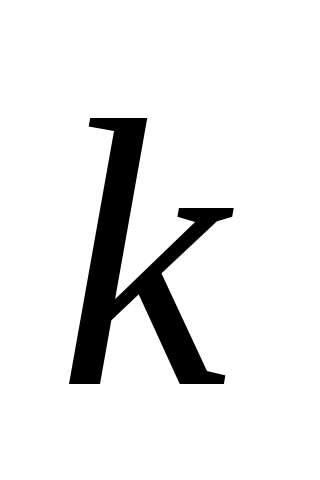 - число коммутаторов на звене А;
- число коммутаторов на звене А; 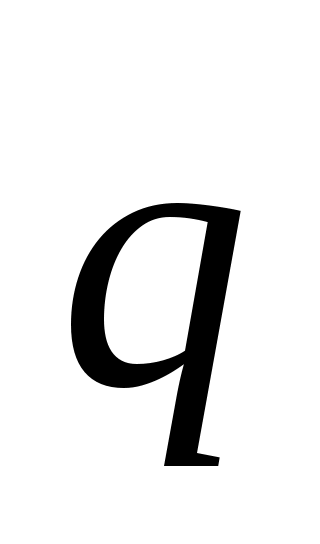 - число выходов, выделяемых в направлении искания из каждого коммутатора звена В;
- число выходов, выделяемых в направлении искания из каждого коммутатора звена В; 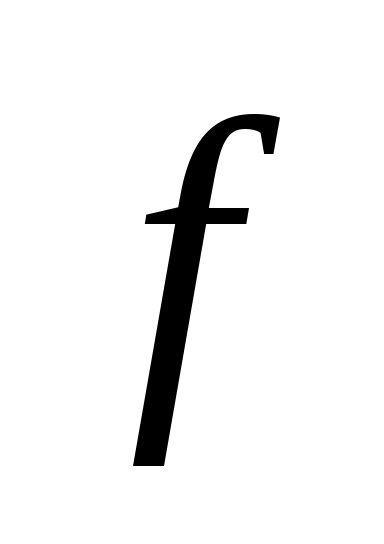 -связность блока;
-связность блока; 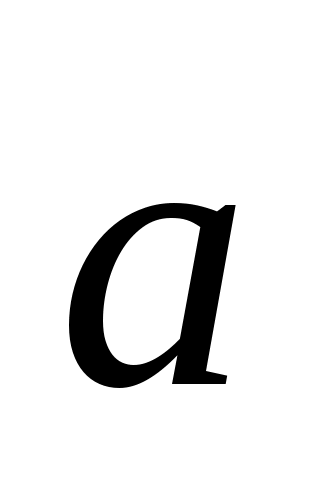 - нагрузка на один вход;
- нагрузка на один вход; 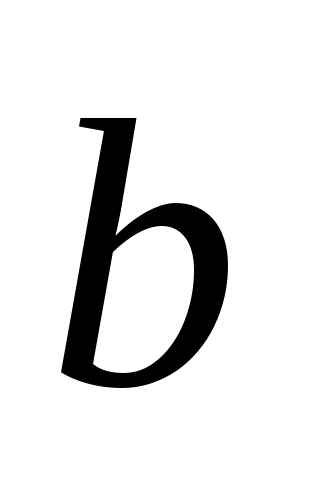 - нагрузка на одну промежуточную линию блока;
- нагрузка на одну промежуточную линию блока; 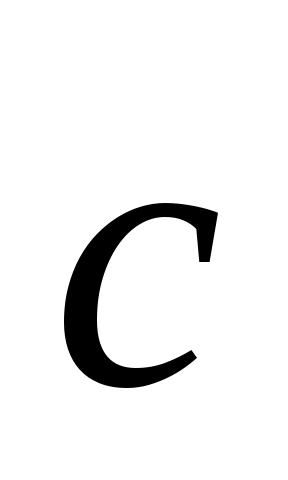 - нагрузка на один выход в направлении искания;
- нагрузка на один выход в направлении искания;  - интенсивность поступающей нагрузки в данном направлении (рис.9.1).
- интенсивность поступающей нагрузки в данном направлении (рис.9.1).
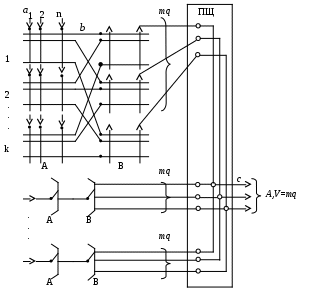
Рис.9.1. Двухзвенное полнодоступное блокируемое включение V=mq.
Если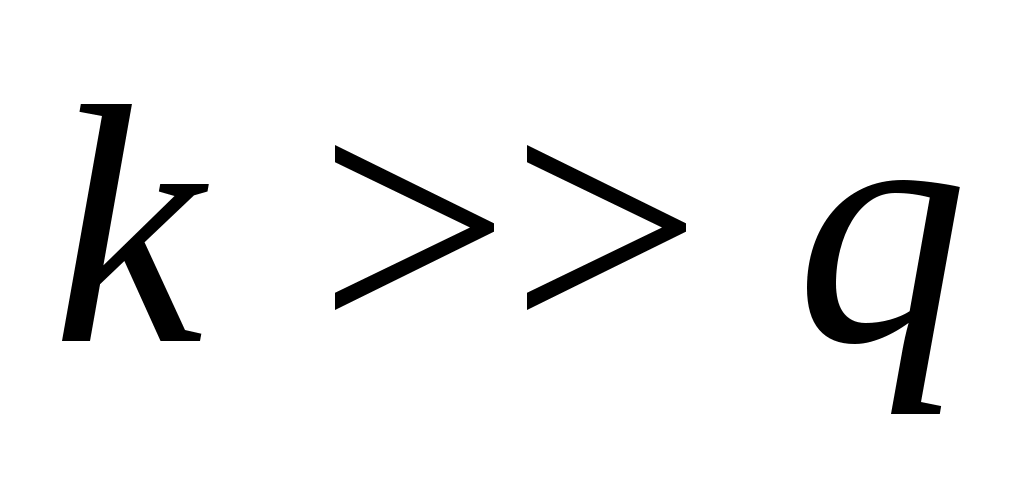 , то на первом звене А применяют распределение Бернулли, на втором звене – распределение Эрланга. Расчетные формулы для вероятности потерь
, то на первом звене А применяют распределение Бернулли, на втором звене – распределение Эрланга. Расчетные формулы для вероятности потерь 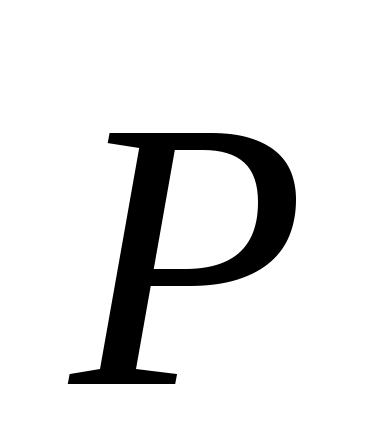 следующие:
следующие:
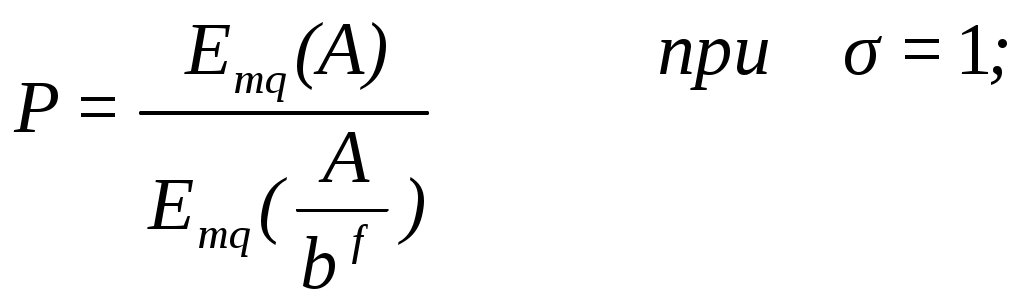 (9.1)
(9.1)
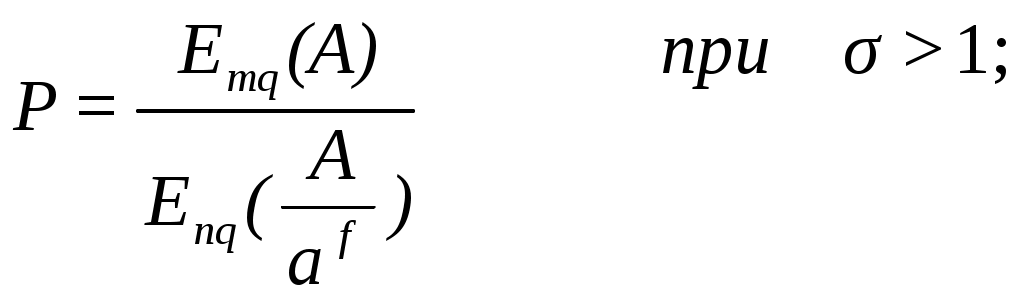 (9.2)
(9.2)
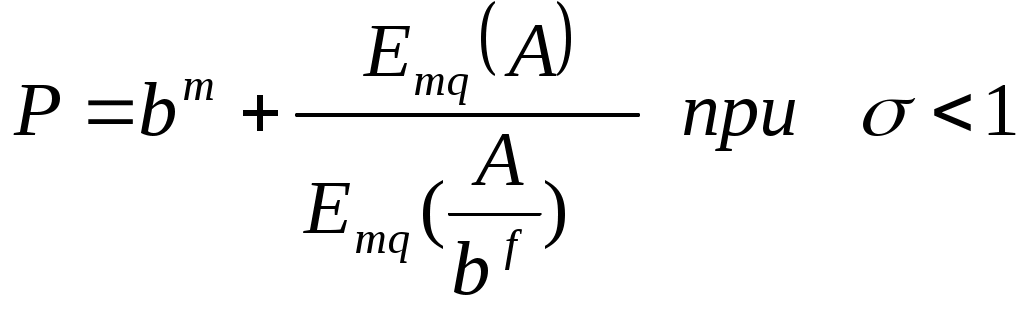 (9.3)
(9.3)
Если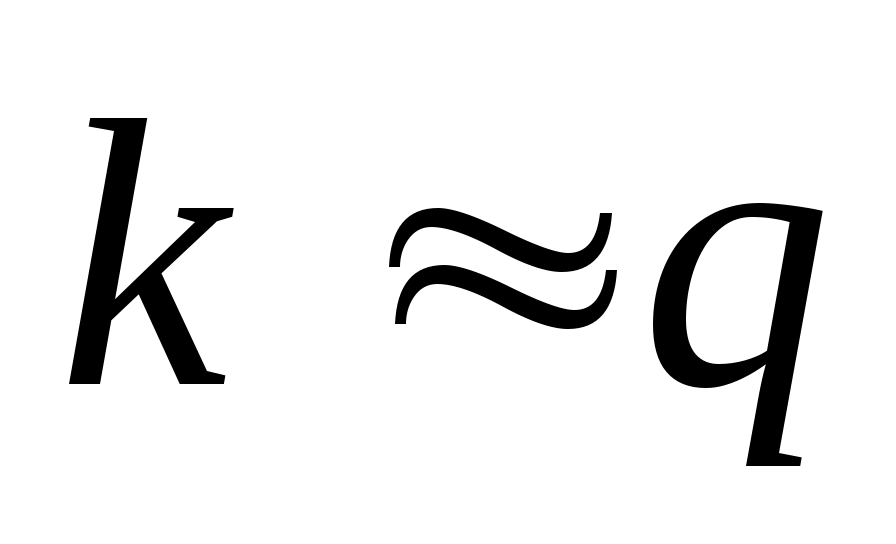 , то на звеньях А и В используется распределение Бернулли. Расчетные формулы следующие:
, то на звеньях А и В используется распределение Бернулли. Расчетные формулы следующие:
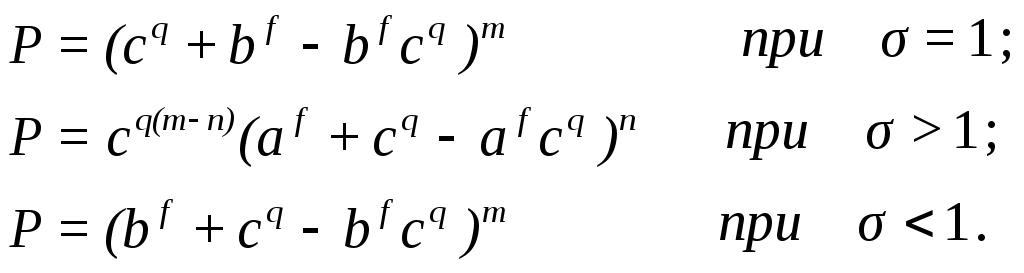 (9.4)
(9.4)
(9.5)
(9.6)
Если величина потерь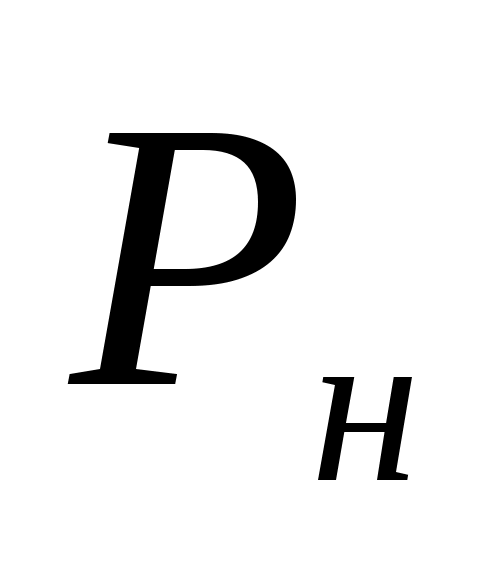 задана, то число линий V=mqиз приведенных уравнений определяется путем подбора такого значения
задана, то число линий V=mqиз приведенных уравнений определяется путем подбора такого значения 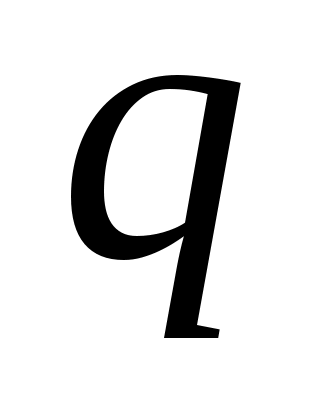
, при котором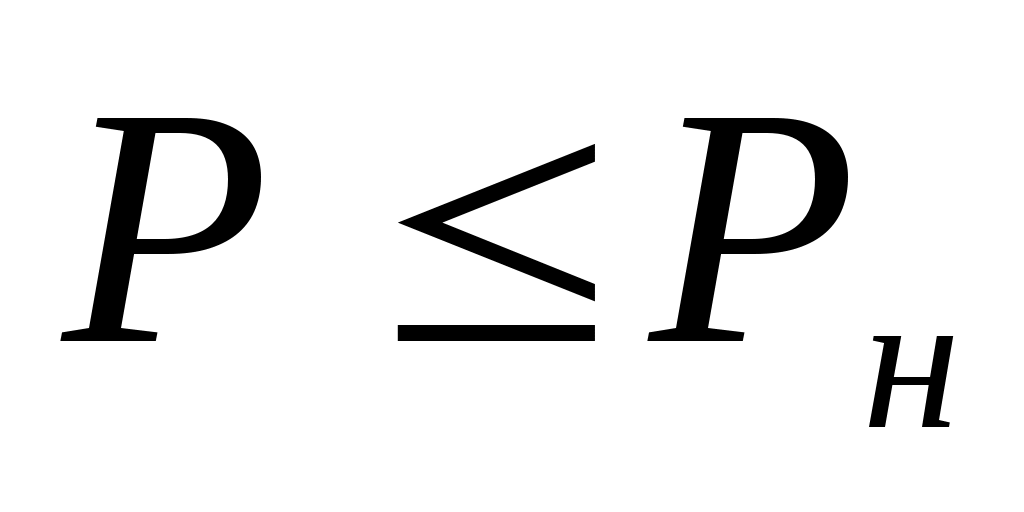 .
.
Задание 9.
1. Для заданного в таблице 6.2. задания 6 двухзвенного блока ГИ построить схему группообразования в координатном виде и рассчитать величину вероятности потерь для направлений к УСС и АМТС при полнодоступном двухзвенном включении линий. Значения интенсивности нагрузок в направлениях к АМТС и УСС взять из результатов расчета задания 3.
2. Для того же двухзвенного блока ГИ найти необходимое число линий в направлении от АТСК-3 к проектируемой АТСЭ-4, предполагая полнодоступное включение, при потерях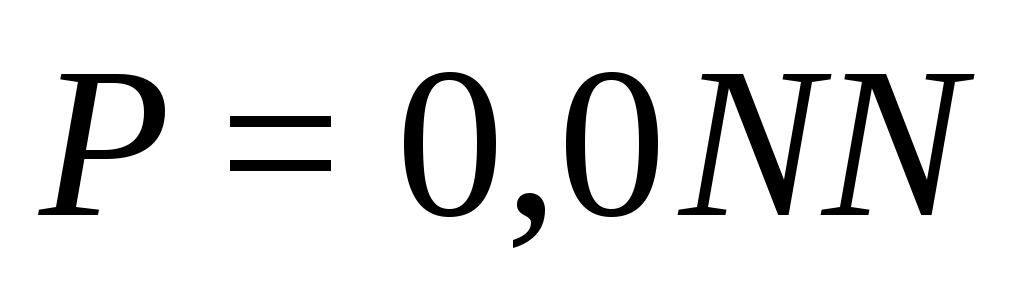 , где
, где  - двухзначный номер варианта.
- двухзначный номер варианта.
Значение интенсивности нагрузки в направлении взять из результатов расчета задания 3. Нагрузку на один вход блока взять из задания 6.
Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий
Неполнодоступное включение линий имеет место при условии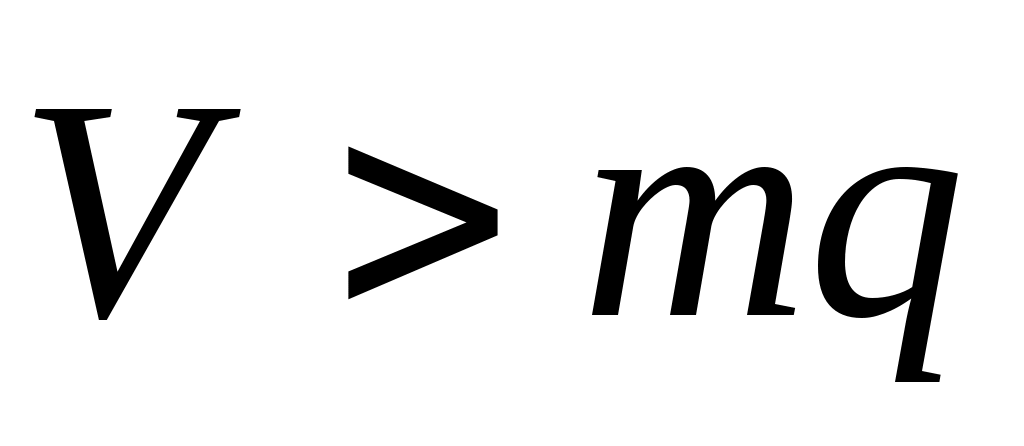 . Это включение аналогично рис.9.1, но на ПЩ выполняется НПД включение
. Это включение аналогично рис.9.1, но на ПЩ выполняется НПД включение 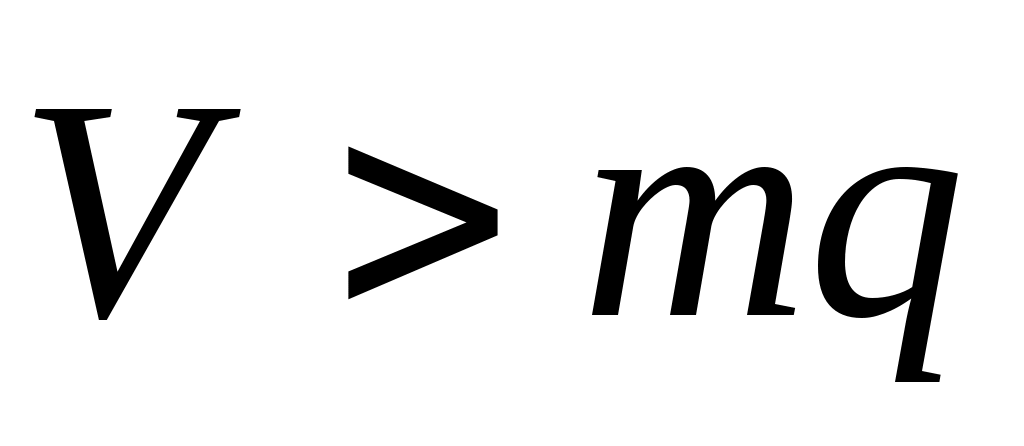 .
.
М
 А
А
етод Якобеуса для расчета неполнодоступных схем основывается на идее О’Делла. Эта идея заключается в том, что средняя нагрузка, обслуженная одной линией неполнодоступного пучка, находится в промежутке между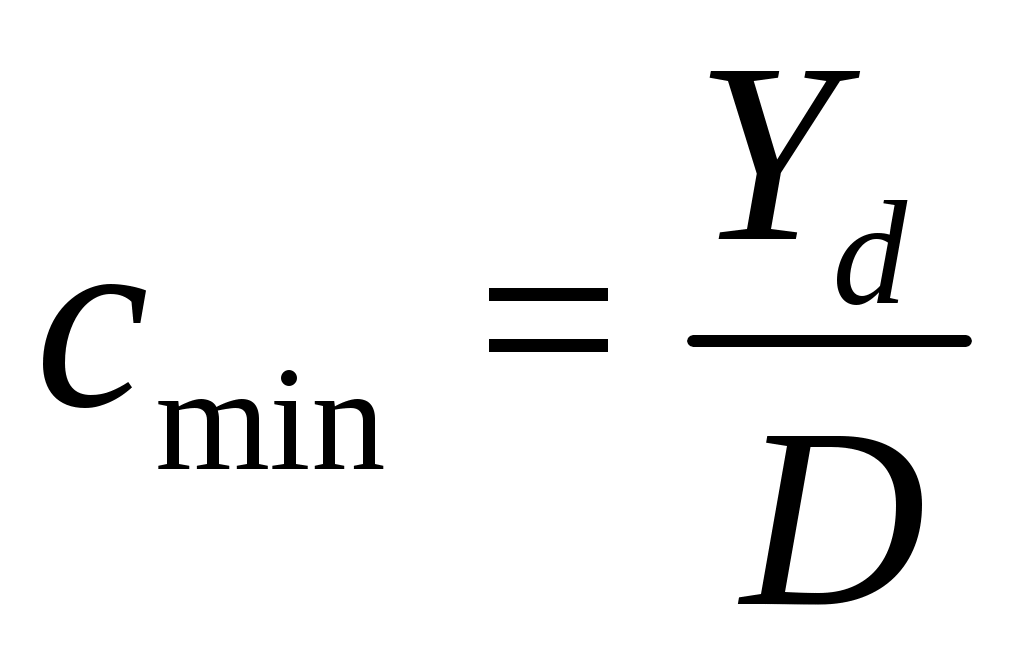 (
(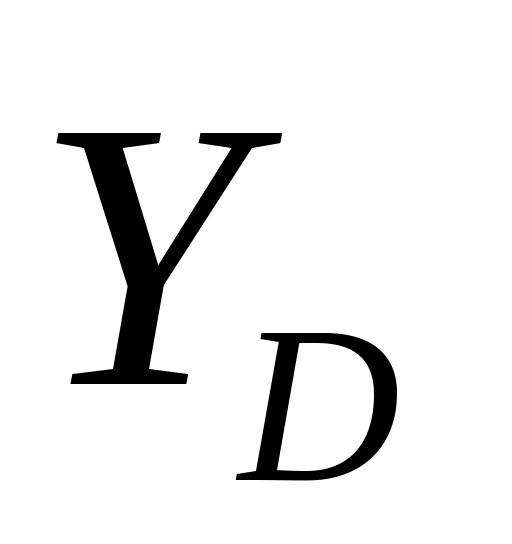 - определяется по 1-ой формуле Эрланга) и максимальным значением
- определяется по 1-ой формуле Эрланга) и максимальным значением 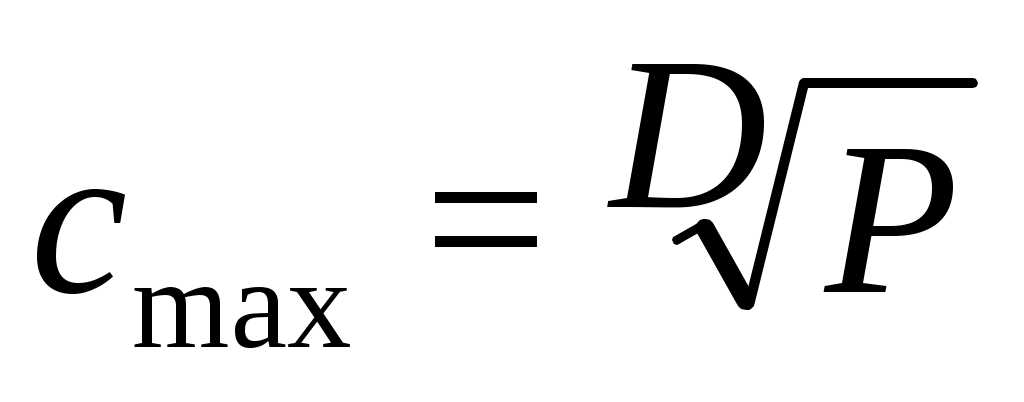 .
.
Величина определяется для случая
определяется для случая 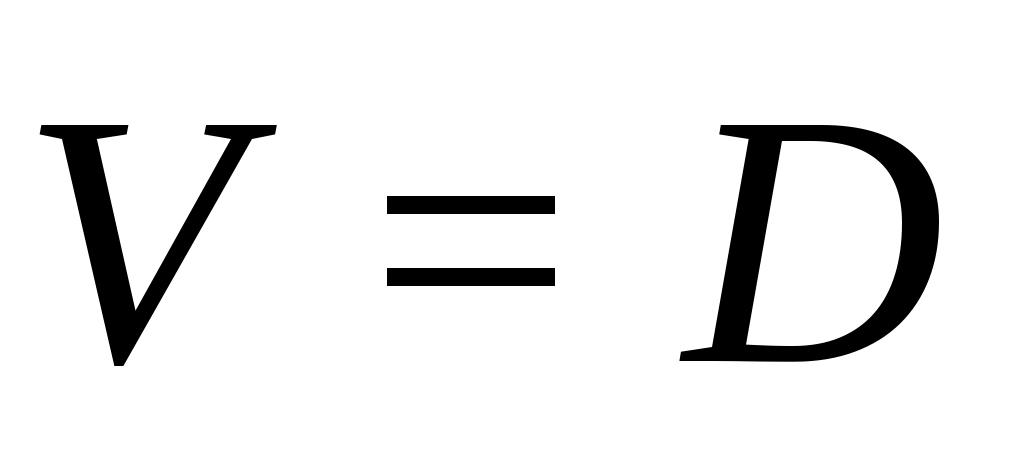 .
.
В соответствии с идеей О’Делла число линий неполнодоступного пучка может быть определено из выражения:
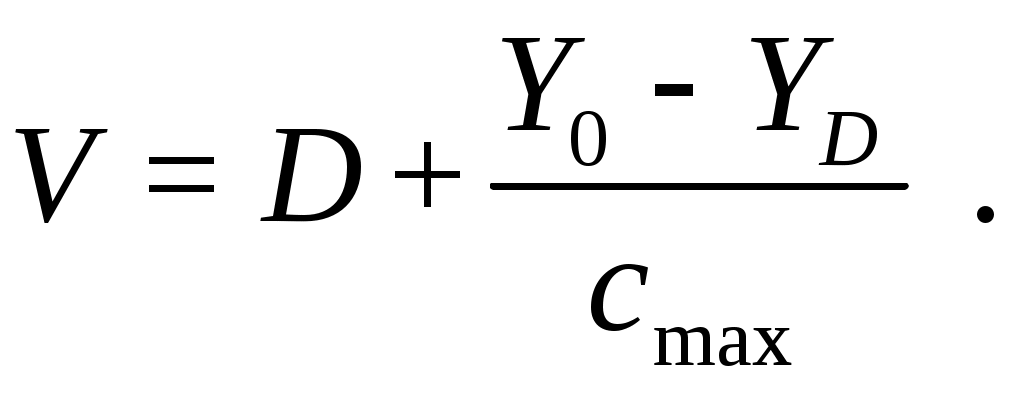 (10.1)
(10.1)
Для двухзвенных схем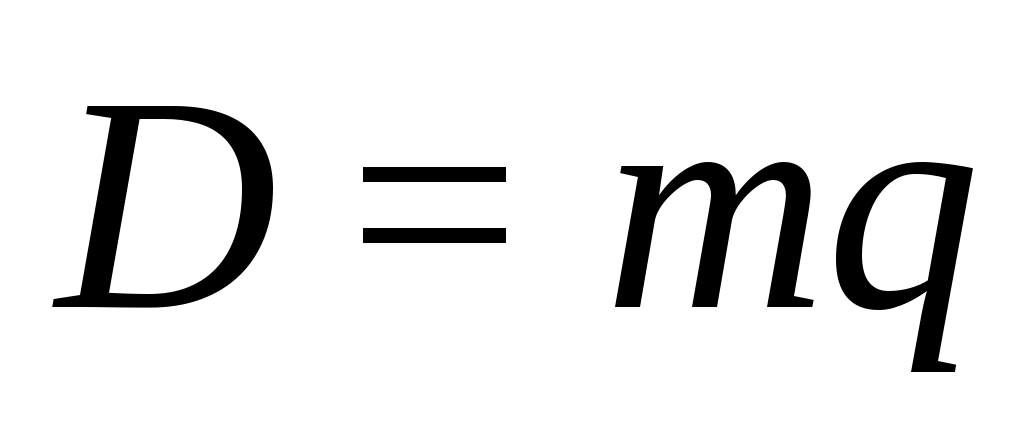 и
и 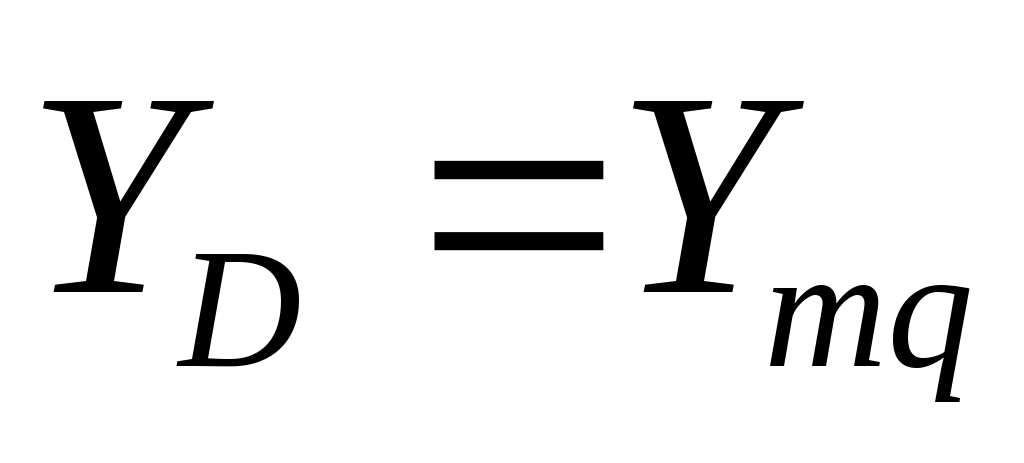 . Для определения
. Для определения 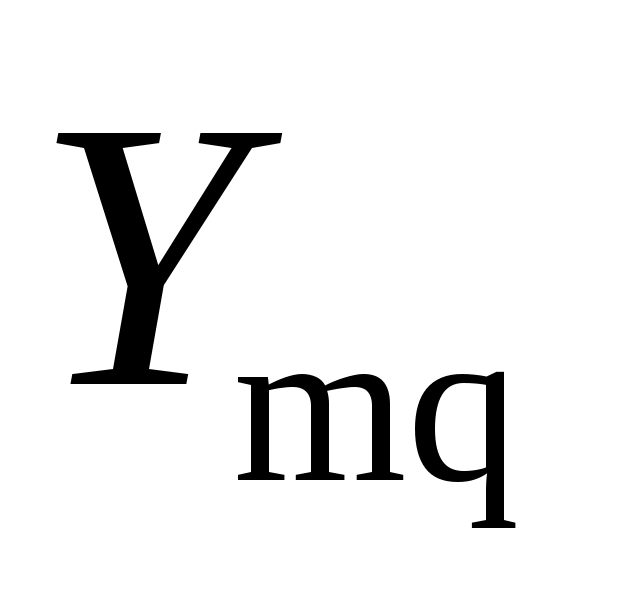 можно воспользоваться соответствующими уравнениями Якобеуса, полученными для двухзвенных схем, в выходы которых включен полнодоступный пучок линий. Например, для
можно воспользоваться соответствующими уравнениями Якобеуса, полученными для двухзвенных схем, в выходы которых включен полнодоступный пучок линий. Например, для 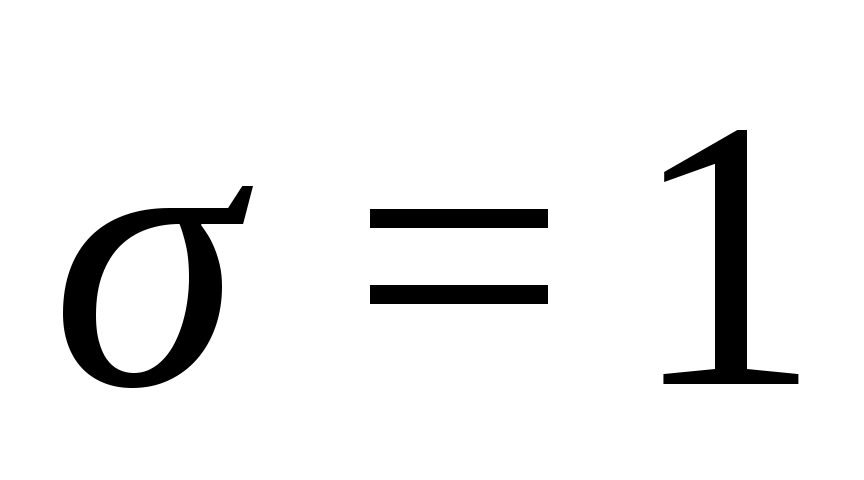 и
и 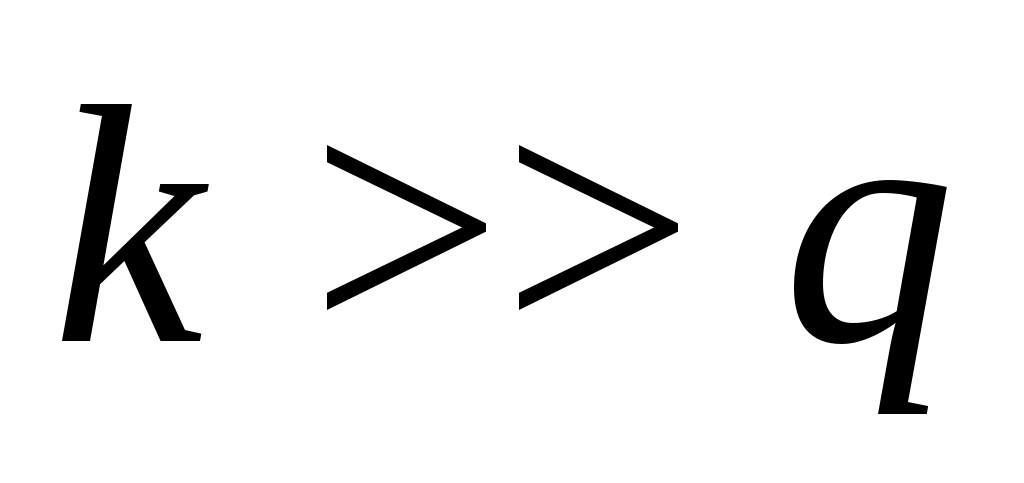 ,
, 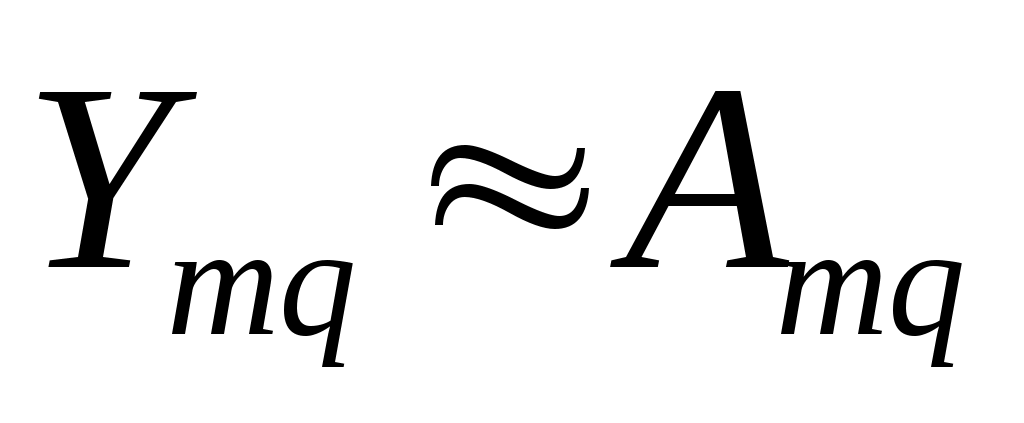 можно определить из уравнения
можно определить из уравнения
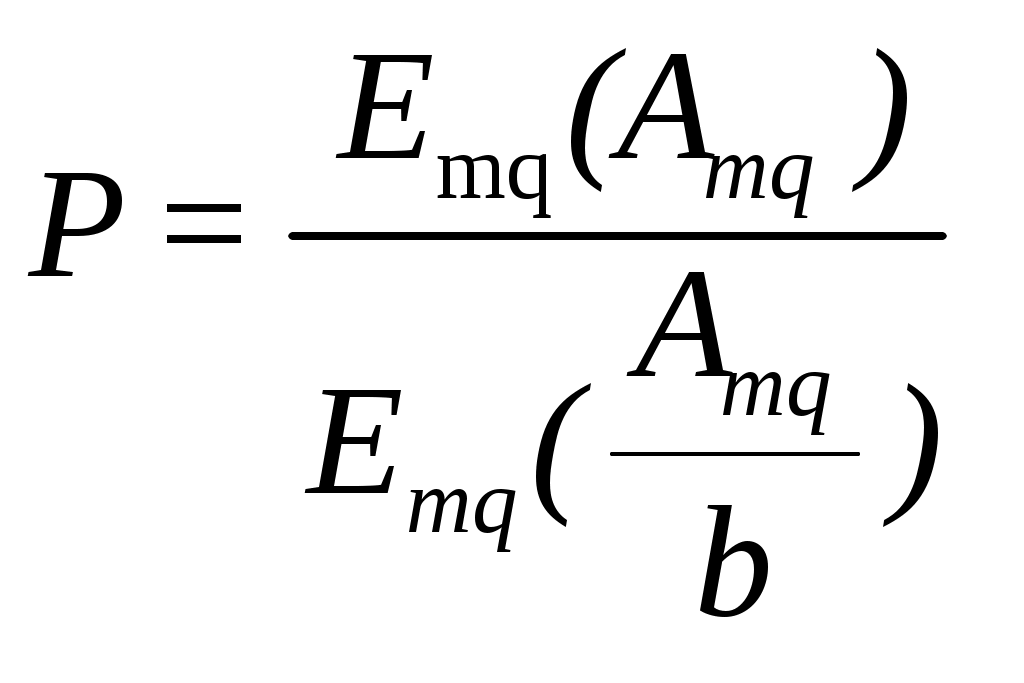 (10.2)
(10.2)
путем подбора при известных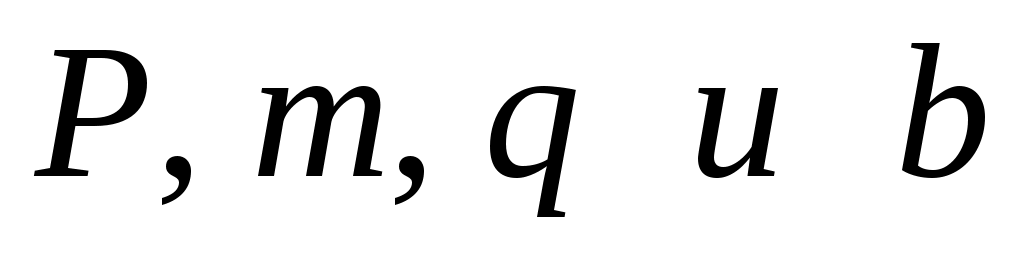 .
.
При определении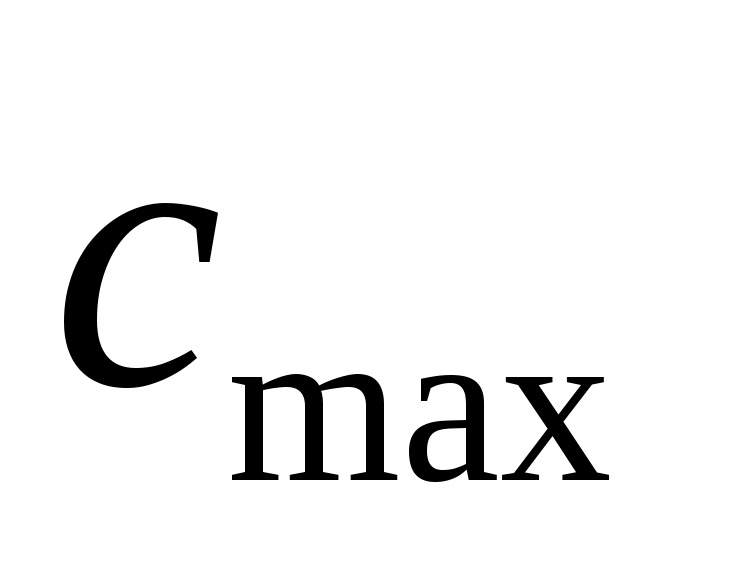 предполагается очень большое число линий
предполагается очень большое число линий 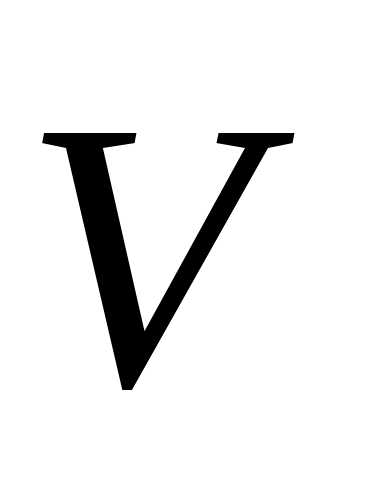 и для нахождения
и для нахождения 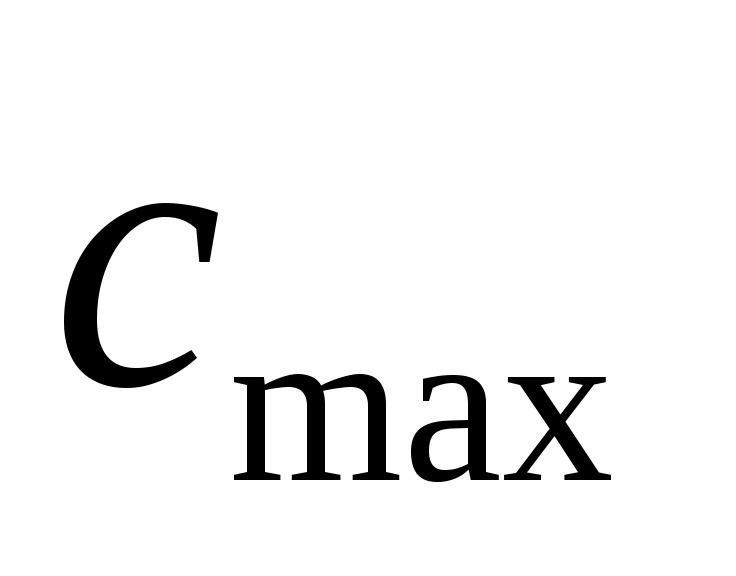 при
при 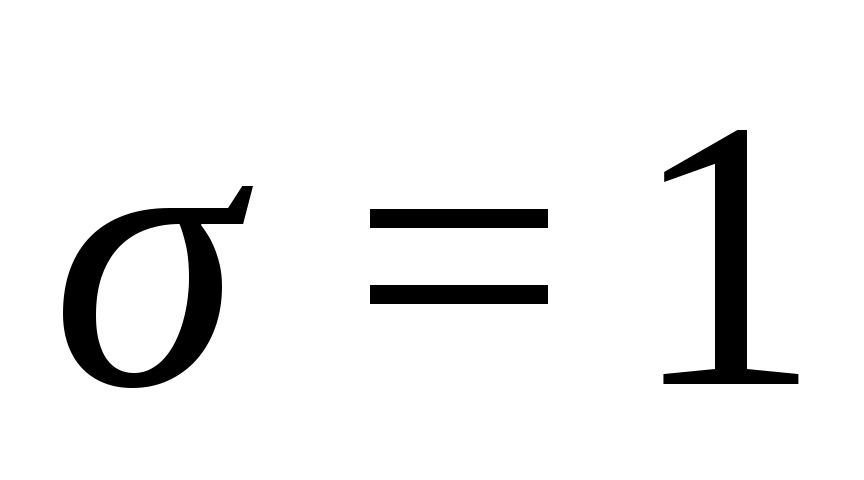 следует воспользоваться формулой Якобеуса для полнодоступного включения, полученной в предположении распределения Бернулли на первом и втором звеньях:
следует воспользоваться формулой Якобеуса для полнодоступного включения, полученной в предположении распределения Бернулли на первом и втором звеньях:
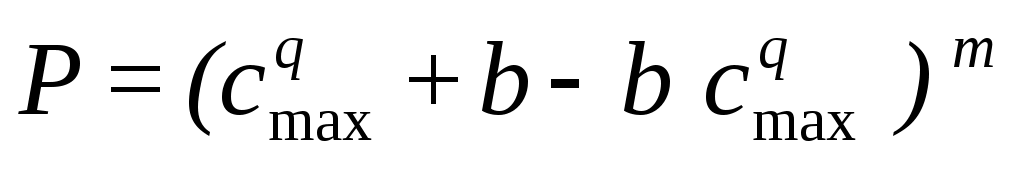 . (10.3)
. (10.3)
Таким образом, для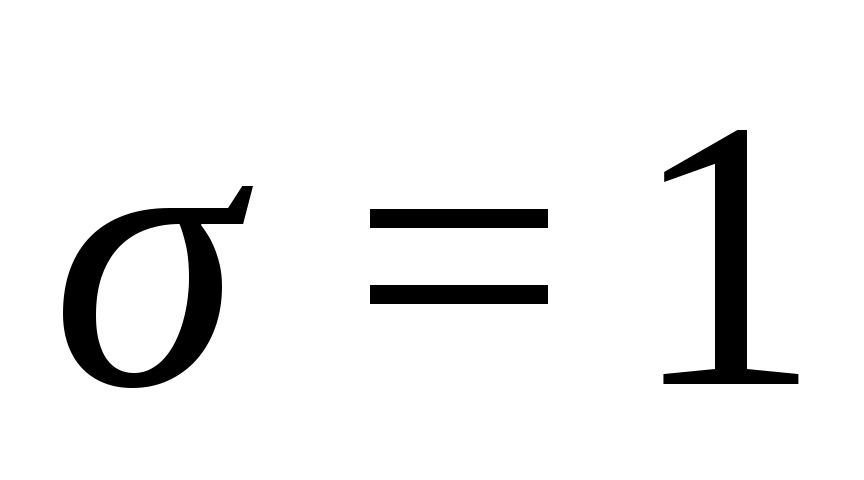 необходимо решить систему уравнений:
необходимо решить систему уравнений:
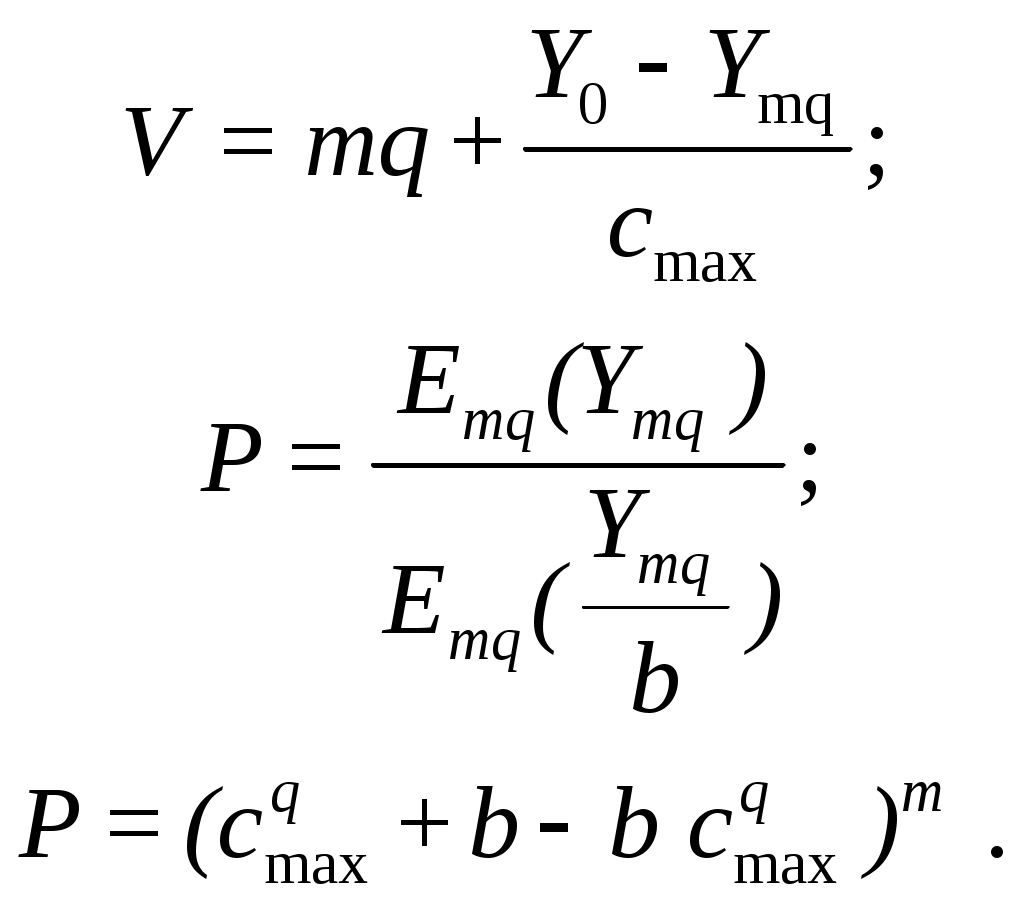 (10.4)
(10.4)
Аналогичным образом получены уравнения для коммутационных двухзвенных схем с расширением и со сжатием:
Для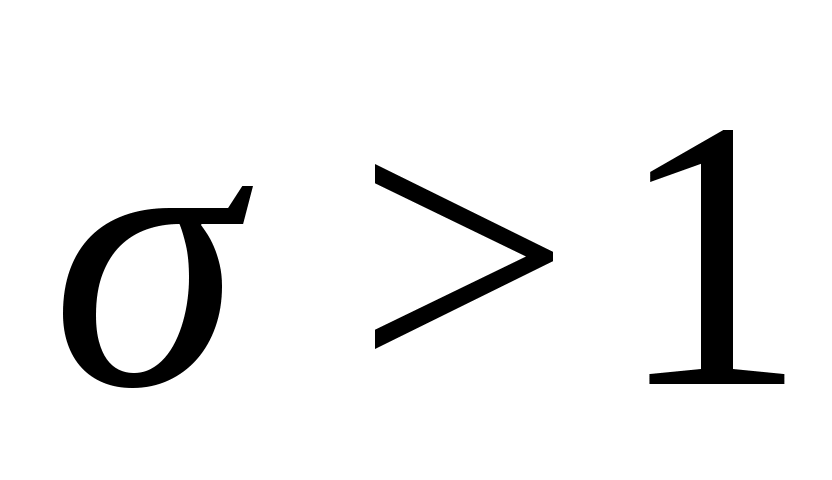
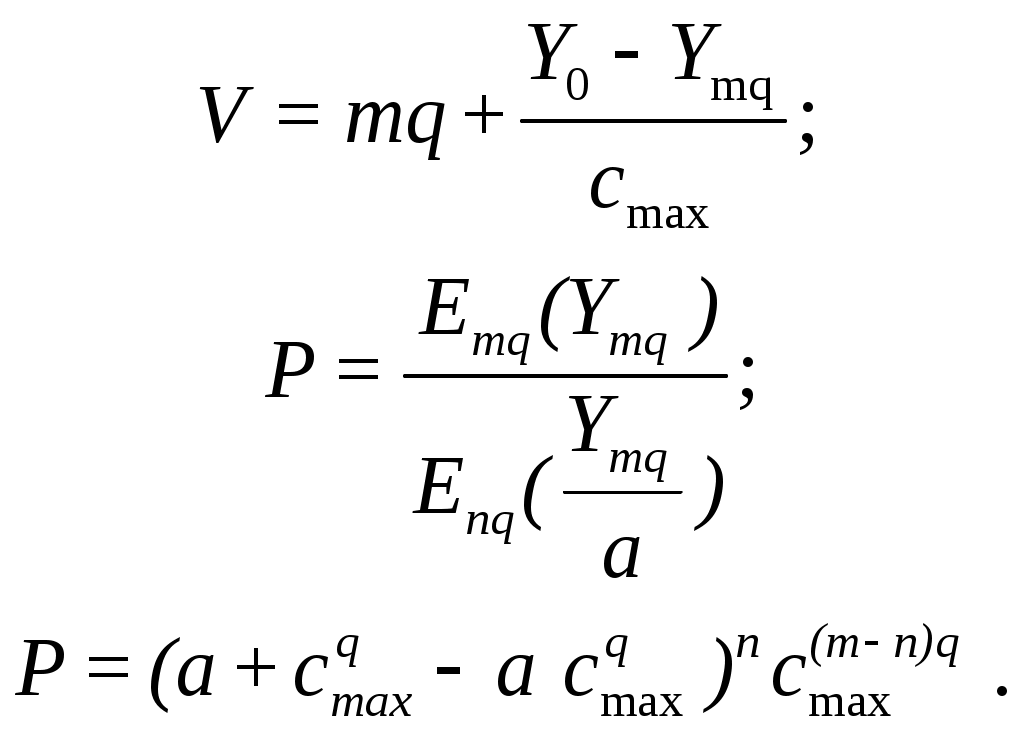 (10.5)
(10.5)
Для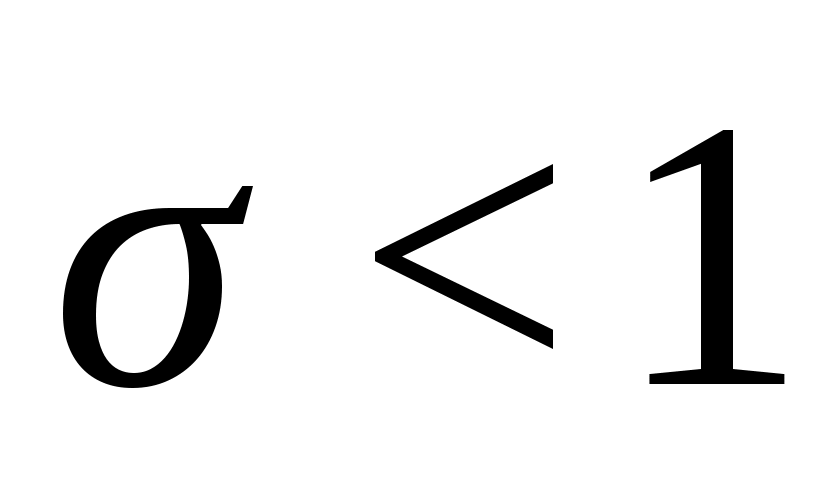

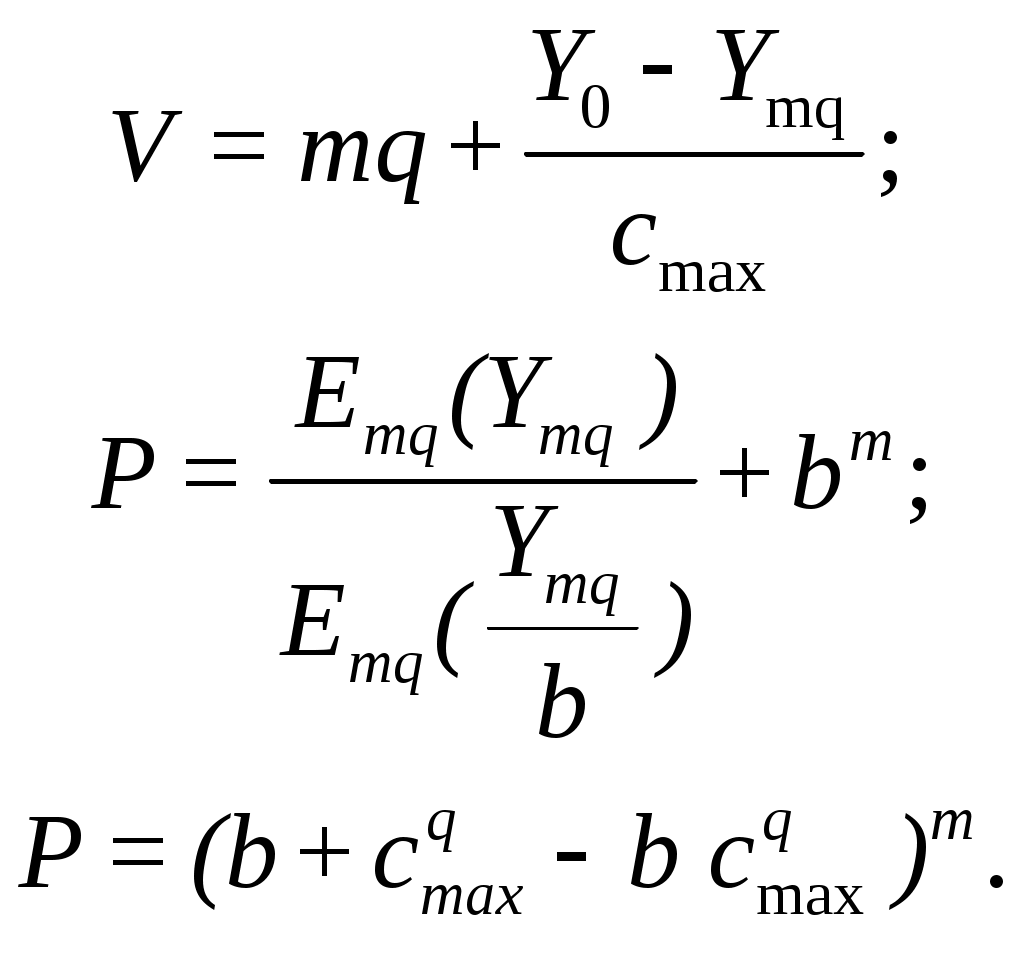 (10.6)
(10.6)
При малой величине потерь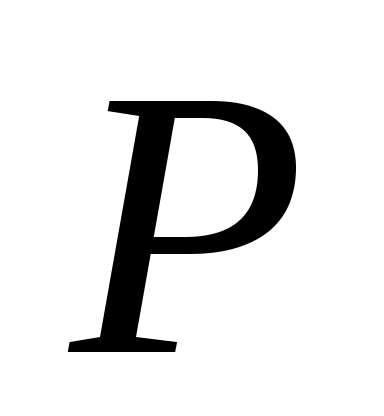 в (10.4) – (10.6) обычно принимается
в (10.4) – (10.6) обычно принимается 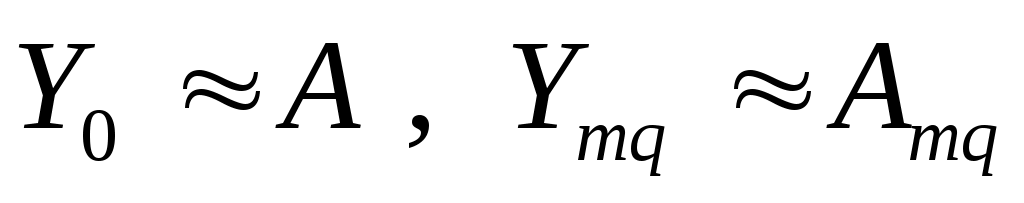 .
.
Порядок решения системы уравнений Якобеуса при определении необходимого числа линий при заданных значениях нагрузки А и качестве обслуживания P следующий:
1)методом подбора с использованием таблиц Пальма [4,8] из второго уравнения системы определяется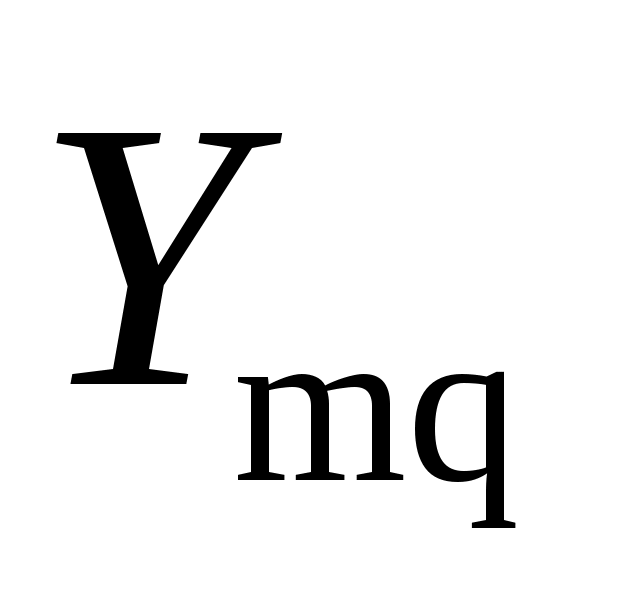
;
2)методом подбора (или решением) из третьего уравнения системы находится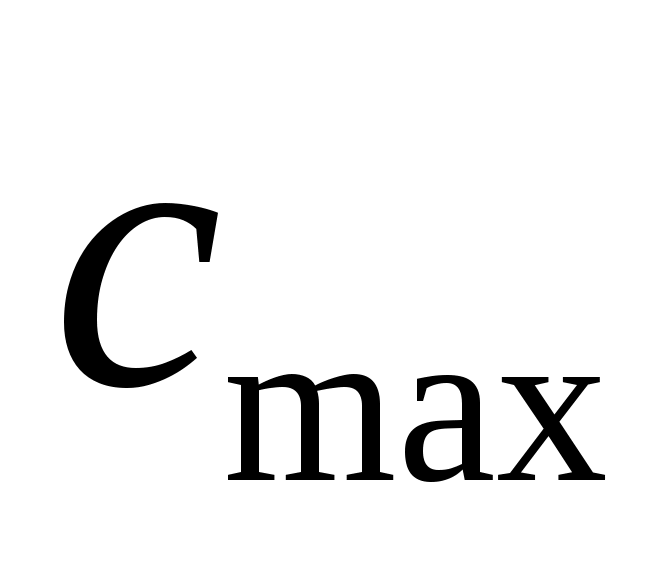 ;
;
3)подставляя полученные значения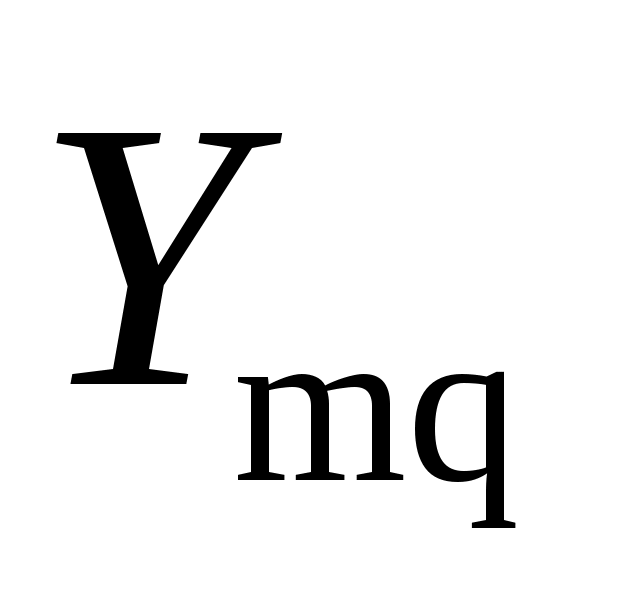 и
и 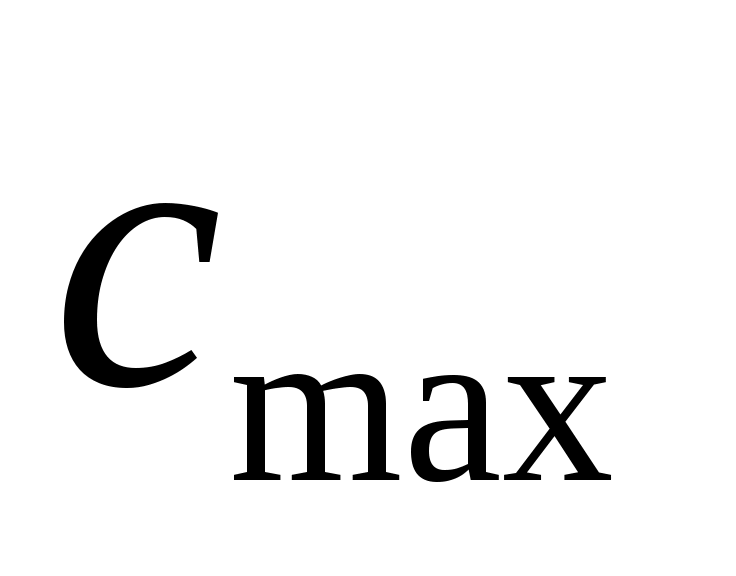 в первое уравнение, определяется число линий
в первое уравнение, определяется число линий 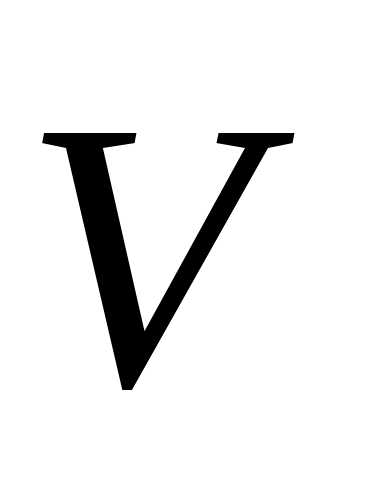 .
.

Рис.9.1. Двухзвенное полнодоступное блокируемое включение V=mq.
Если
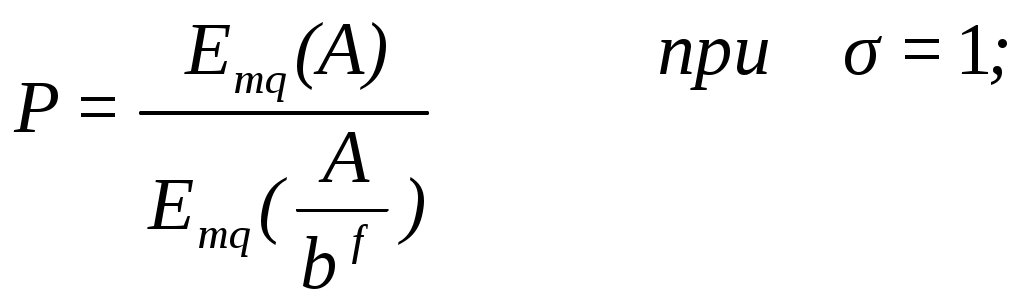 (9.1)
(9.1)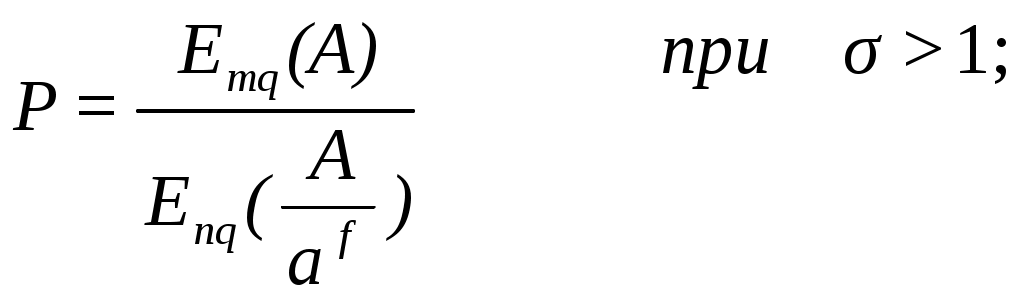 (9.2)
(9.2) 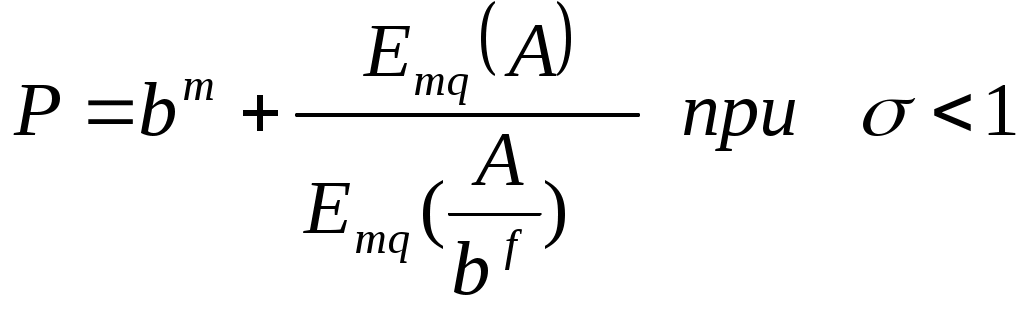 (9.3)
(9.3)Если
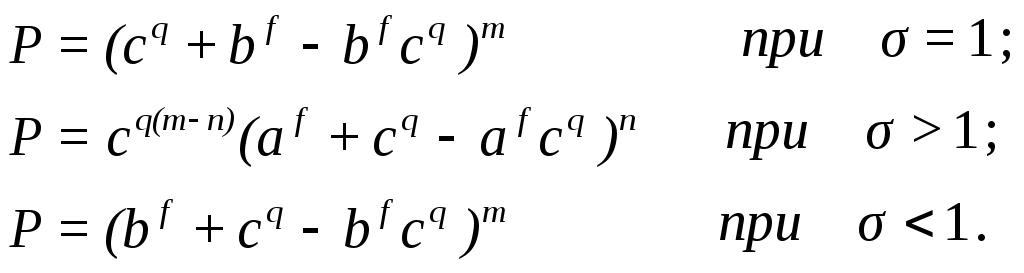 (9.4)
(9.4)(9.5)
(9.6)
Если величина потерь
, при котором
Задание 9.
1. Для заданного в таблице 6.2. задания 6 двухзвенного блока ГИ построить схему группообразования в координатном виде и рассчитать величину вероятности потерь для направлений к УСС и АМТС при полнодоступном двухзвенном включении линий. Значения интенсивности нагрузок в направлениях к АМТС и УСС взять из результатов расчета задания 3.
2. Для того же двухзвенного блока ГИ найти необходимое число линий в направлении от АТСК-3 к проектируемой АТСЭ-4, предполагая полнодоступное включение, при потерях
Значение интенсивности нагрузки в направлении взять из результатов расчета задания 3. Нагрузку на один вход блока взять из задания 6.
Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий
10.1. Метод Якобеуса
Неполнодоступное включение линий имеет место при условии
М
етод Якобеуса для расчета неполнодоступных схем основывается на идее О’Делла. Эта идея заключается в том, что средняя нагрузка, обслуженная одной линией неполнодоступного пучка, находится в промежутке между
Величина
В соответствии с идеей О’Делла число линий неполнодоступного пучка может быть определено из выражения:
Для двухзвенных схем
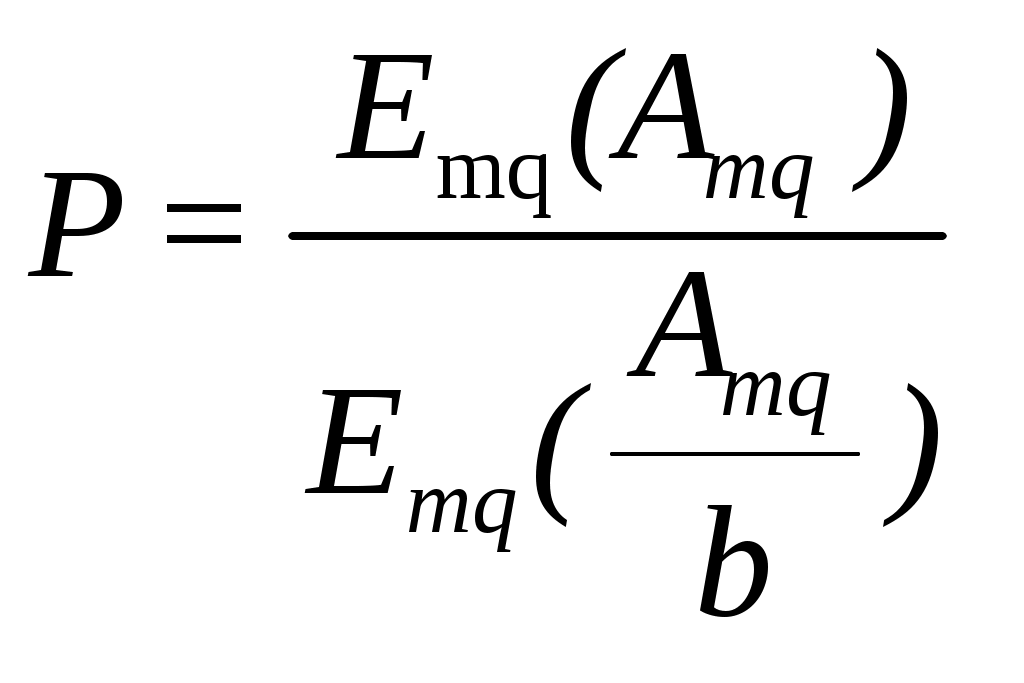 (10.2)
(10.2)путем подбора при известных
При определении
Таким образом, для
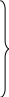
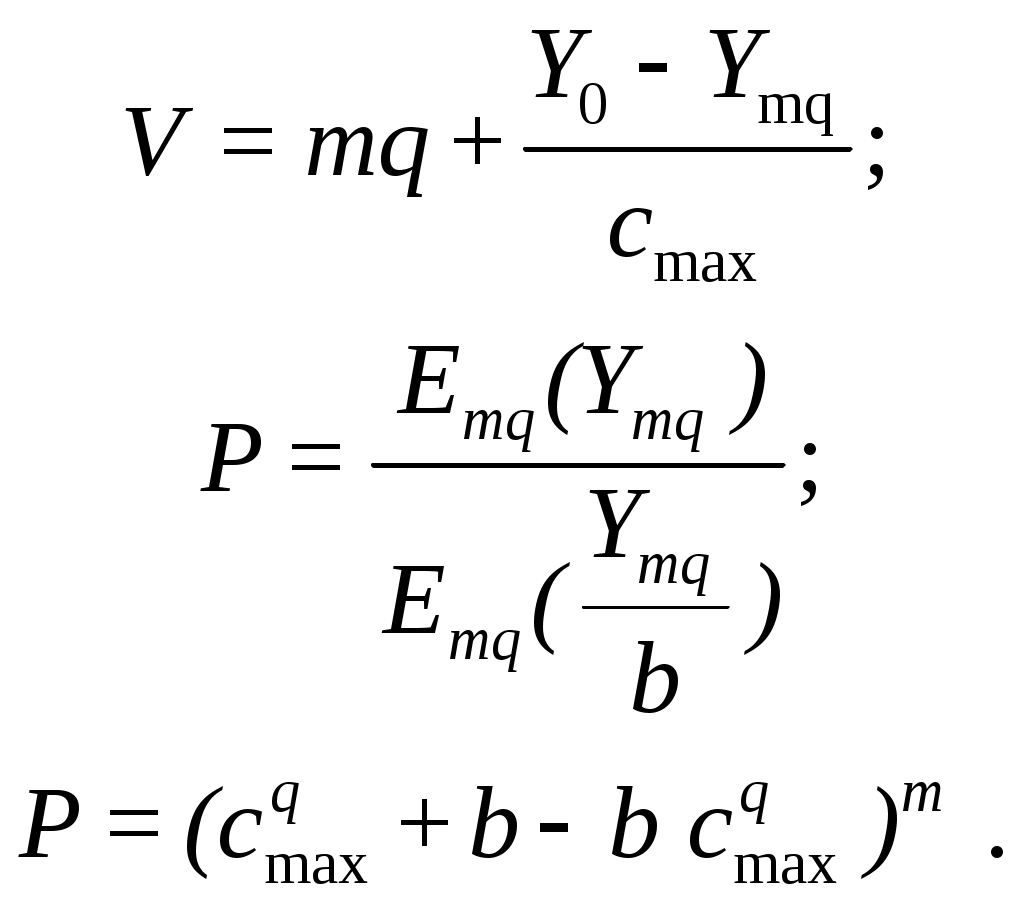 (10.4)
(10.4)Аналогичным образом получены уравнения для коммутационных двухзвенных схем с расширением и со сжатием:
Для
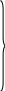
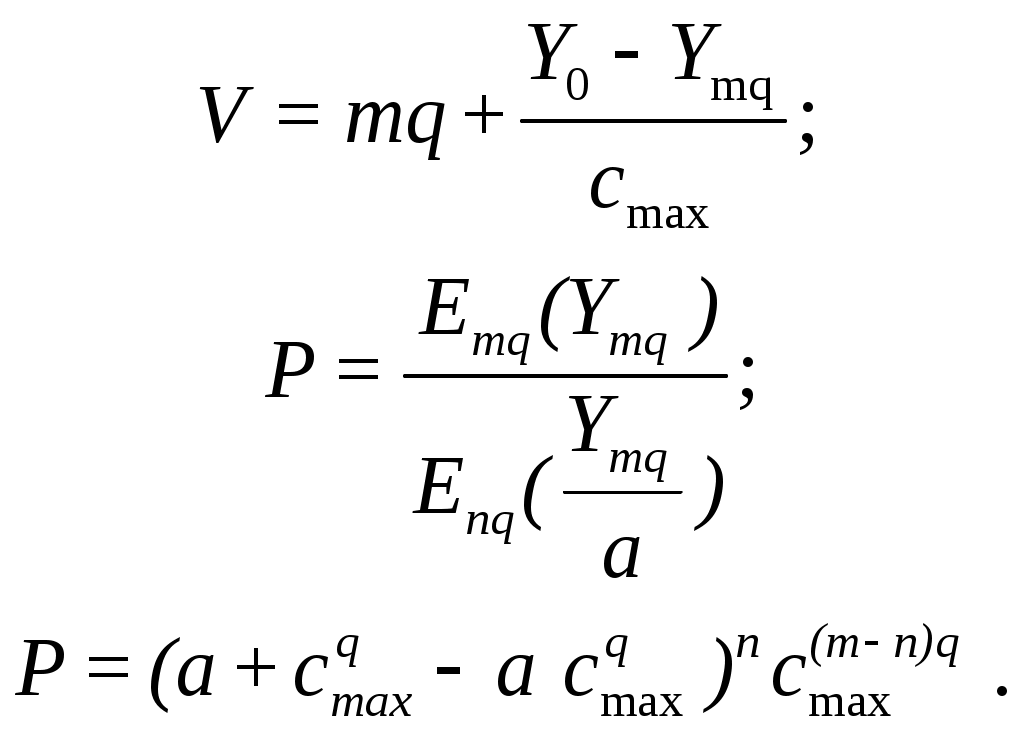 (10.5)
(10.5)Для

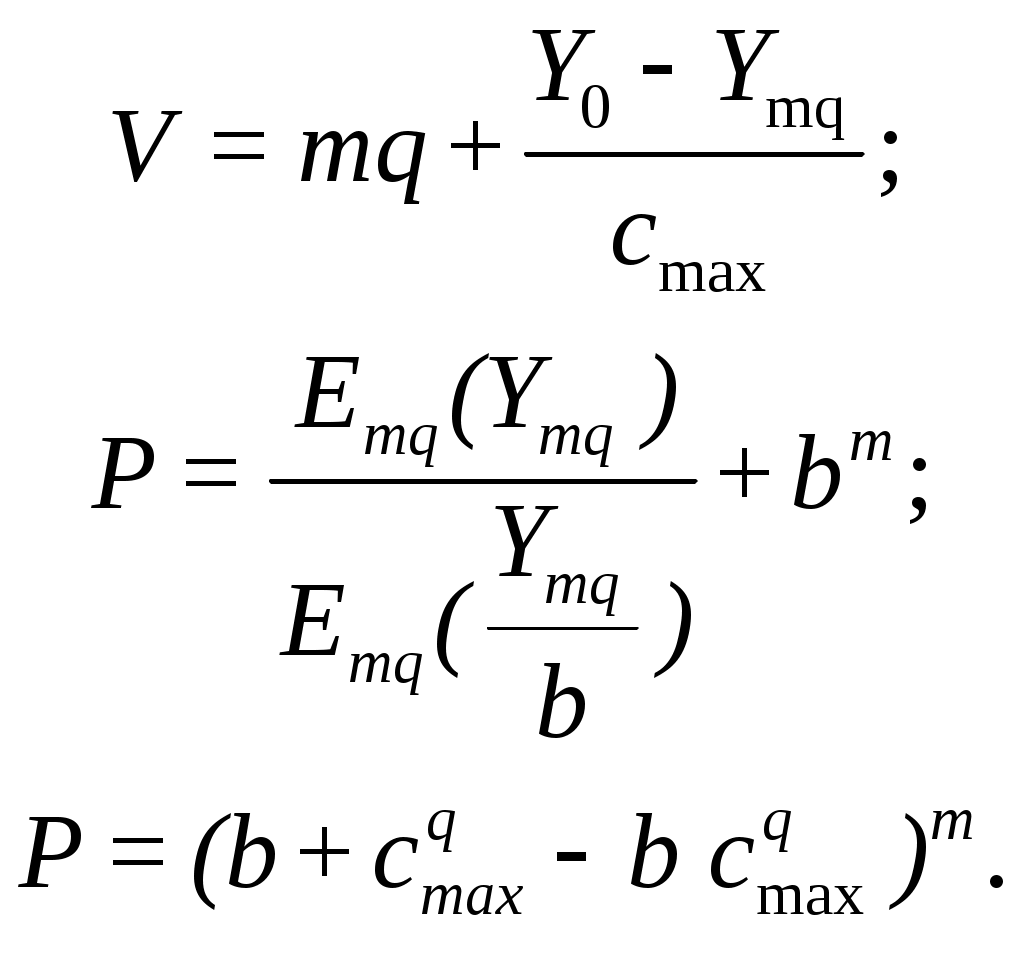 (10.6)
(10.6)При малой величине потерь
Порядок решения системы уравнений Якобеуса при определении необходимого числа линий при заданных значениях нагрузки А и качестве обслуживания P следующий:
1)методом подбора с использованием таблиц Пальма [4,8] из второго уравнения системы определяется
;
2)методом подбора (или решением) из третьего уравнения системы находится
3)подставляя полученные значения
