Файл: Задача 1 растяжение и сжатие стержней для заданной шарнирно стержневой системы требуется.doc
Добавлен: 05.05.2024
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Q пересекает свою ось. Определим ординату сечения 5-5 из уравнения
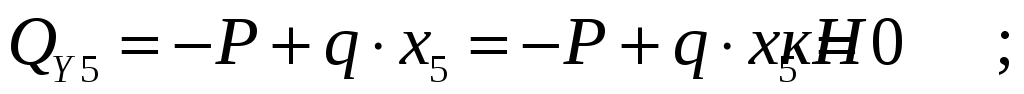
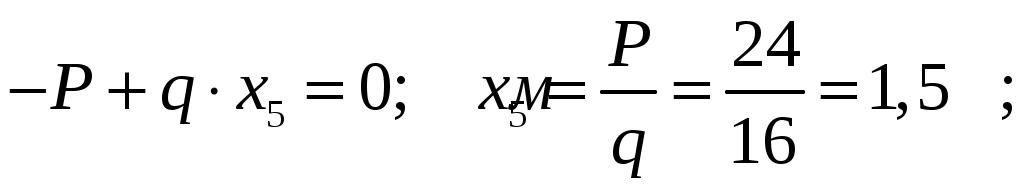
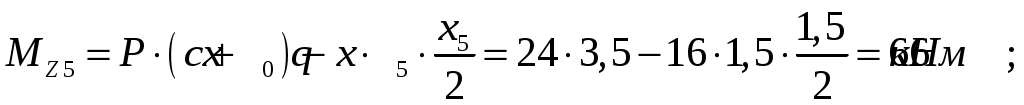
По вычисленным значениям строим эпюры внутренних усилий.
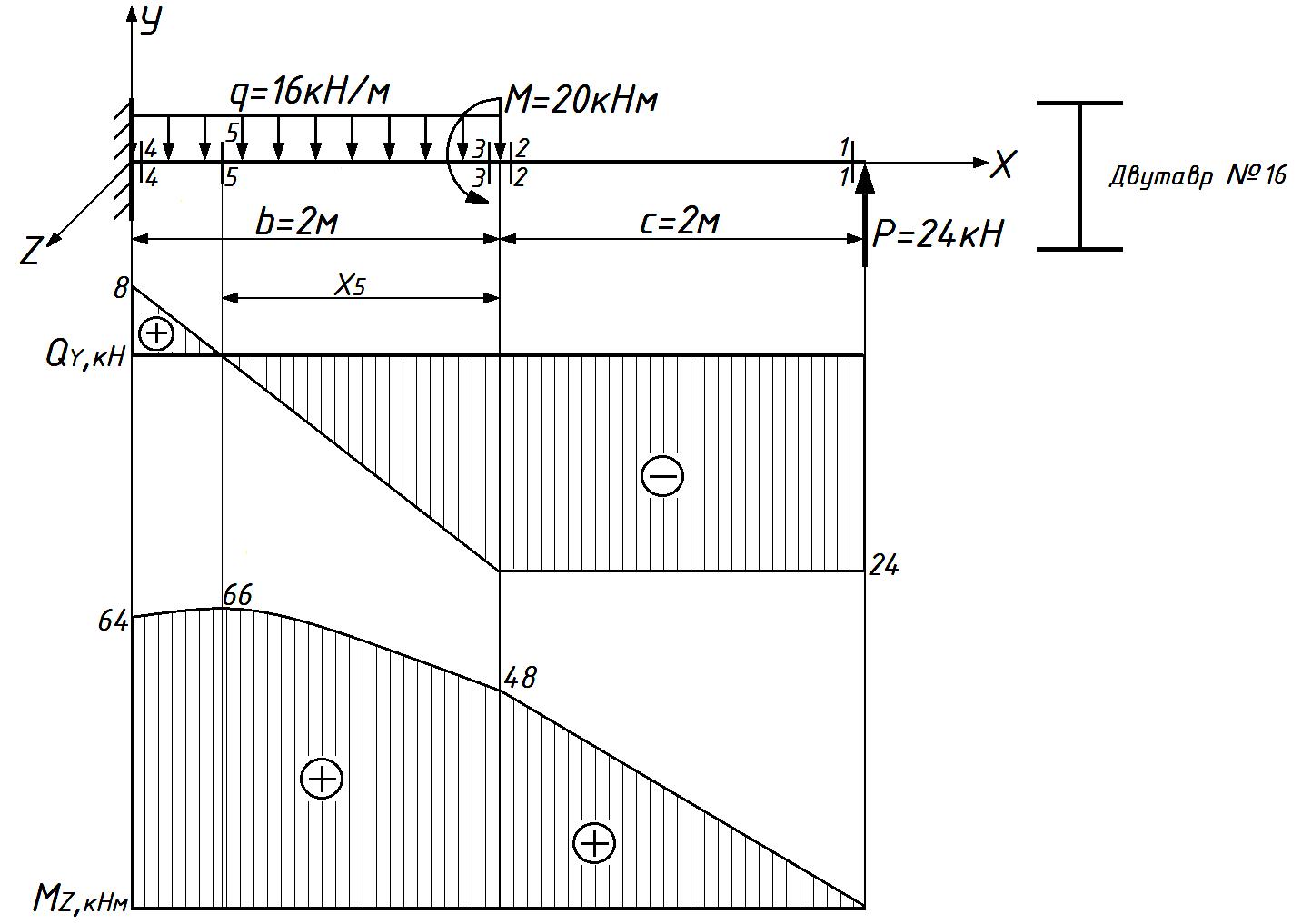
Рисунок 5 – Расчетная схема консольной балки и эпюры внутренних усилий
Условие прочности по нормальным напряжениям при прямом изгибе для балок из пластичных материалов имеет вид:
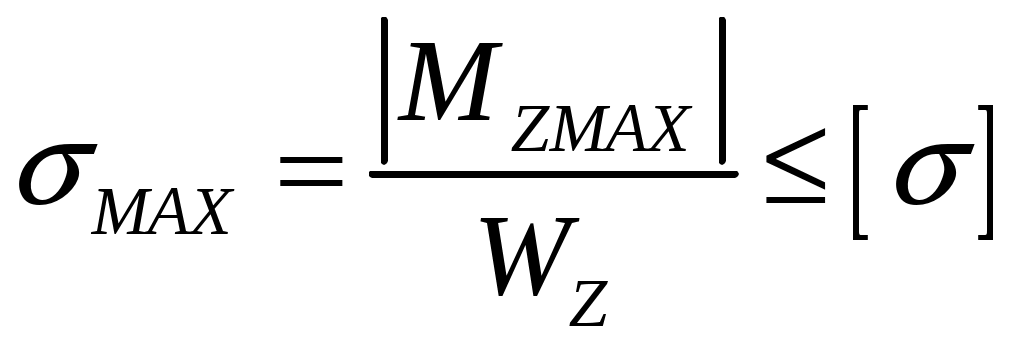 ,
,
где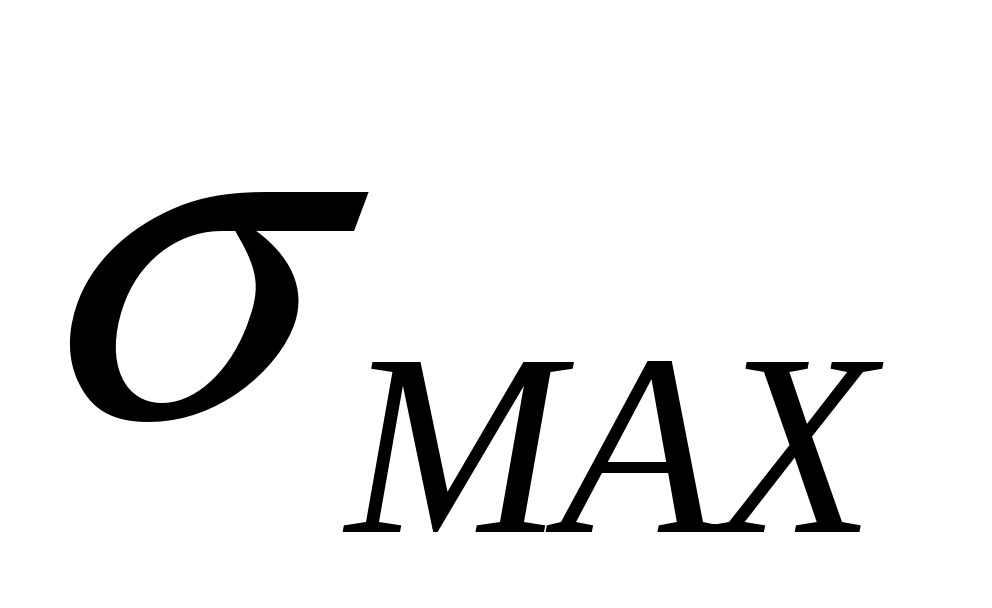 - абсолютное значение наибольшего нормального напряжения, МПа;
- абсолютное значение наибольшего нормального напряжения, МПа;
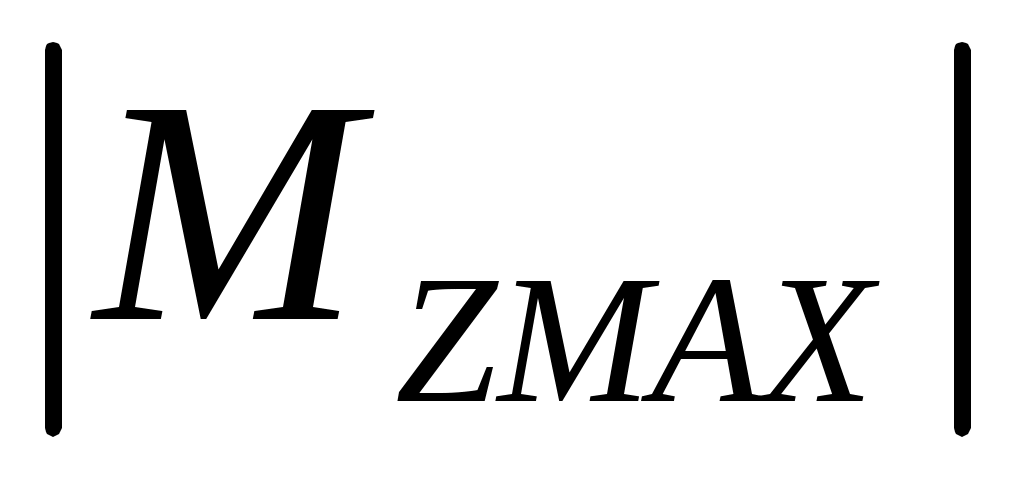 - абсолютное значение наибольшего изгибающего момента относительно главной оси инерции Z сечения балки, кНм.
- абсолютное значение наибольшего изгибающего момента относительно главной оси инерции Z сечения балки, кНм. 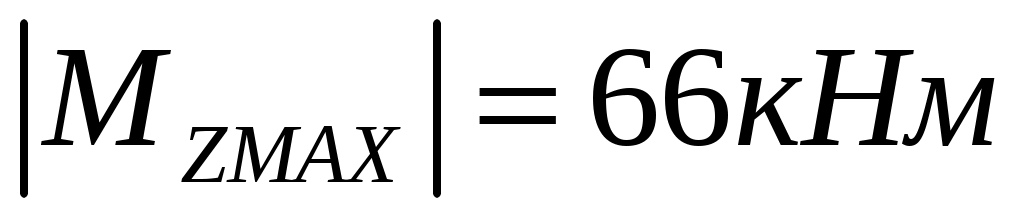 для опасного сечения 5-5.
для опасного сечения 5-5.
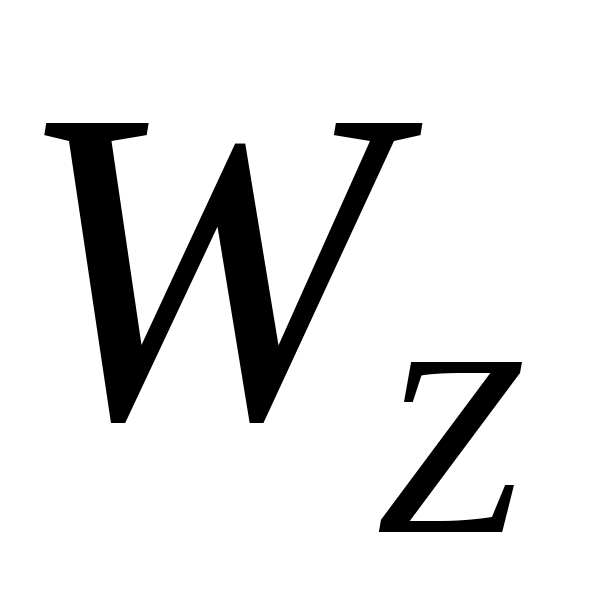 - осевой момент сопротивления сечения изгибу относительно главной оси инерции Z сечения балки, м3. Для заданного двутавра № 16 по ГОСТ8239-89
- осевой момент сопротивления сечения изгибу относительно главной оси инерции Z сечения балки, м3. Для заданного двутавра № 16 по ГОСТ8239-89 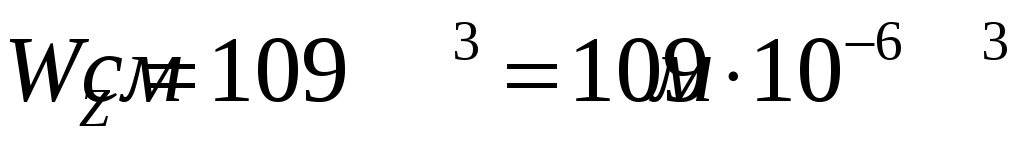 .
.
Определим абсолютное значение наибольшего нормального напряжения в опасном сечении балки и сравним его с допускаемым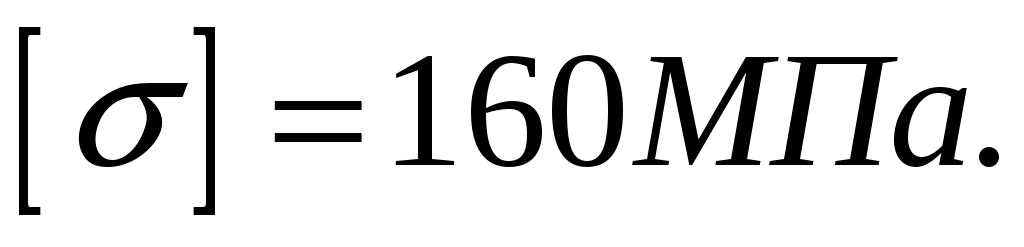
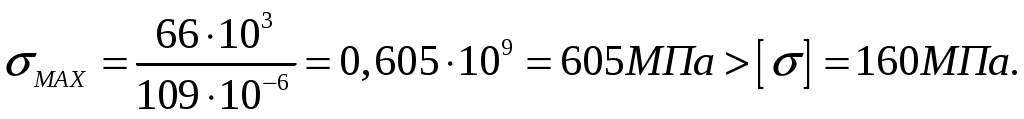
Условие прочности не выполняется. Необходимо принять двутавр не менее № 30, для которого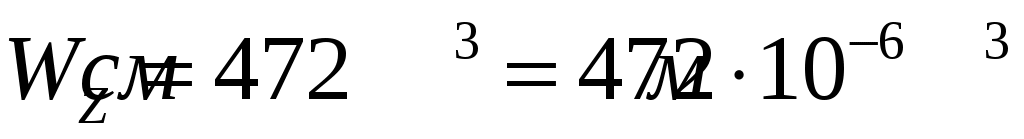 , тогда
, тогда
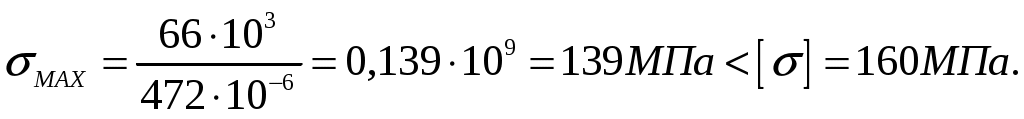
Расчет двух опорной балки
Двух опорная балка имеет три участка, различающихся характером нагружения, а следовательно, и законами изменения поперечных сил и изгибающих моментов.
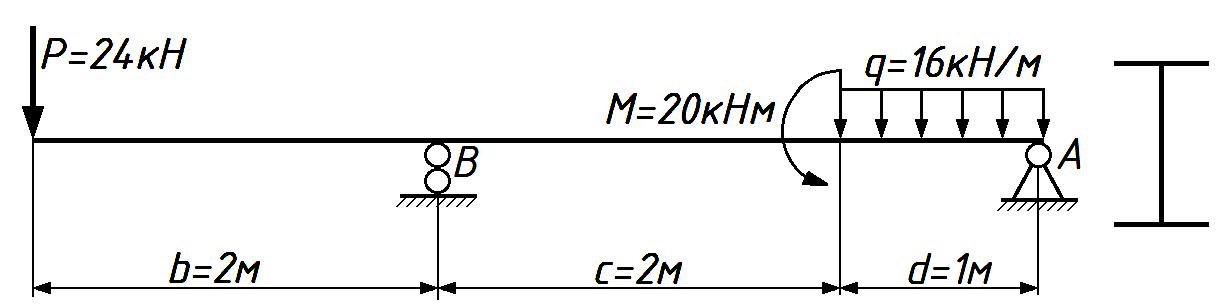
Рисунок 6. – Схема двух опорной балки
Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения.
О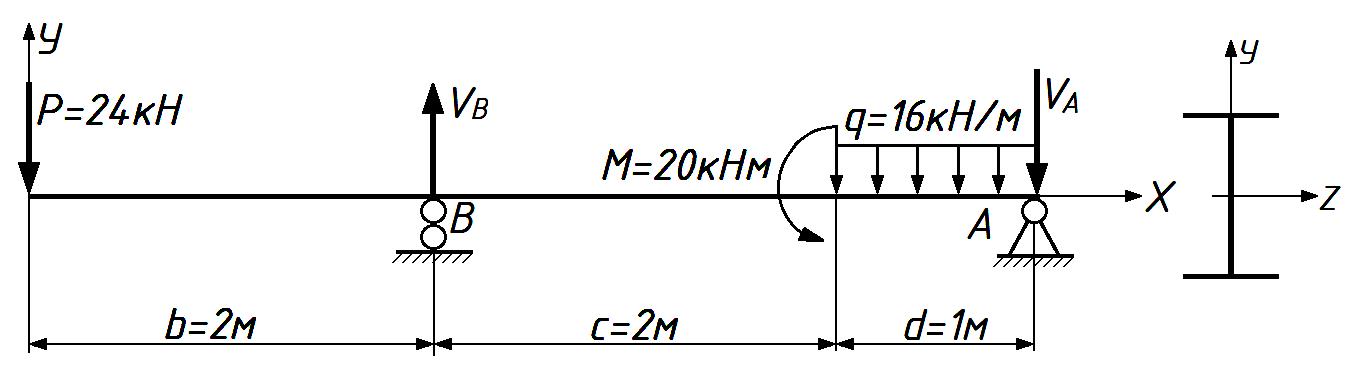 пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют).
пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют).
Рисунок 7. – Расчетная схема двухопорной балки
Составим уравнения равновесия:
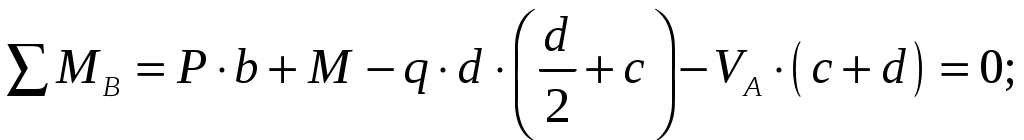
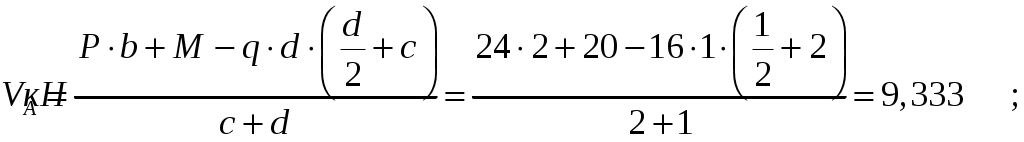
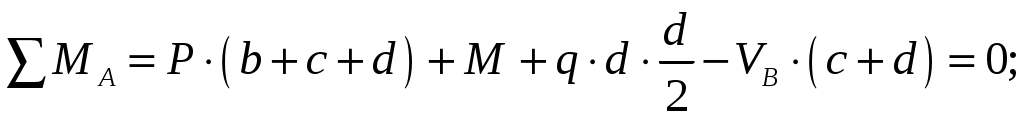
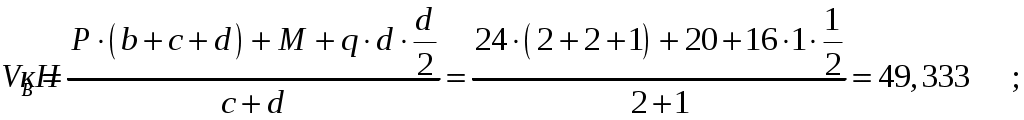
Для проверки правильности полученных результатов составим третье уравнение равновесия, спроецировав все силы на ось У:
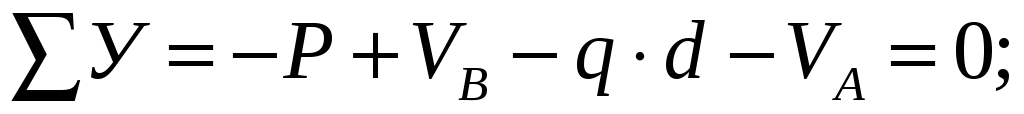
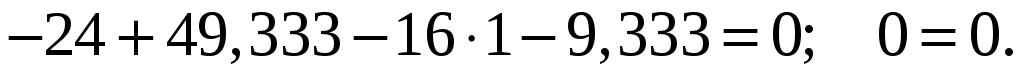
Опорные реакции найдены верно.
Проведем характерные сечения и находим внутренние усилия в этих сечениях.
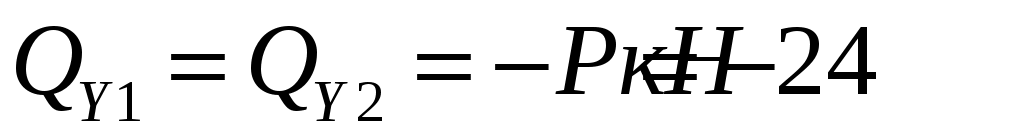
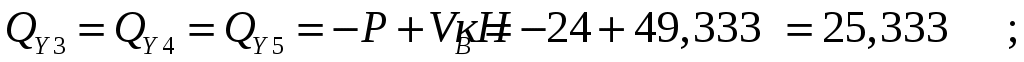
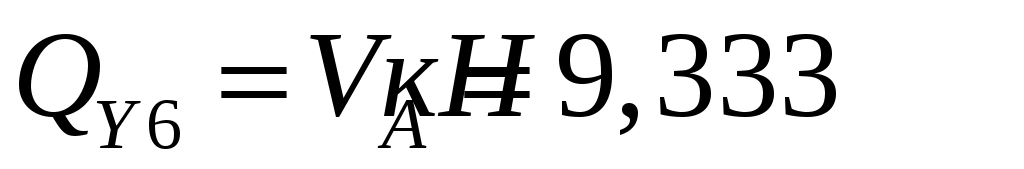
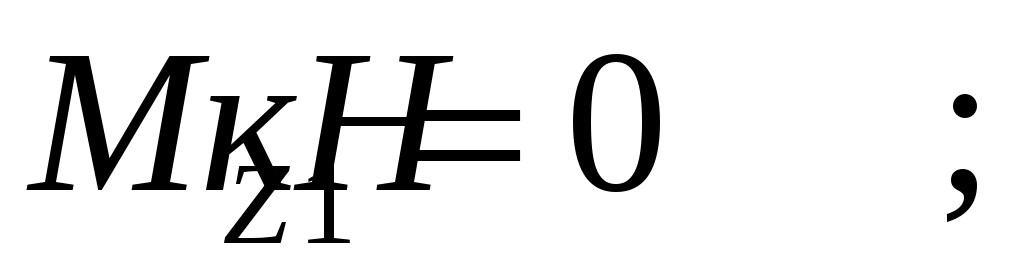
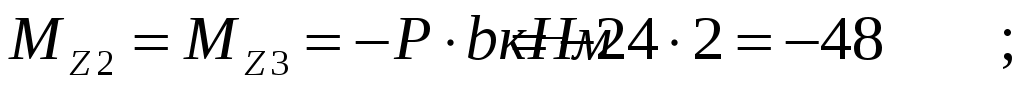
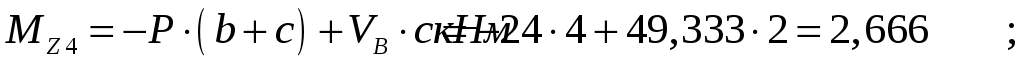
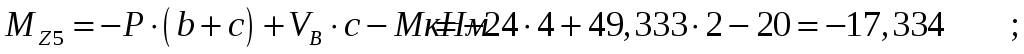
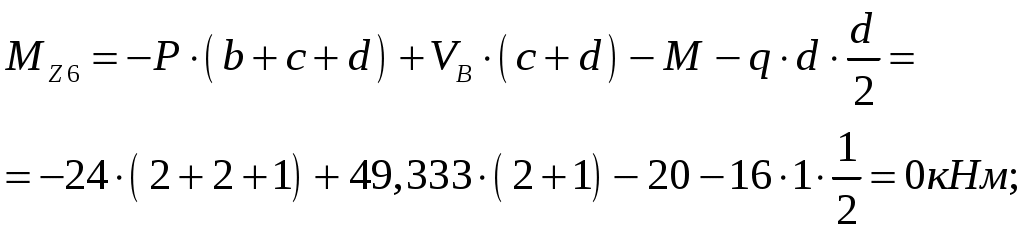
По вычисленным значениям построим эпюры внутренних усилий.
Опасными сечениями балки являются сечения 2-2 и 3-3.В них действует наибольший по абсолютному значению изгибающий момент
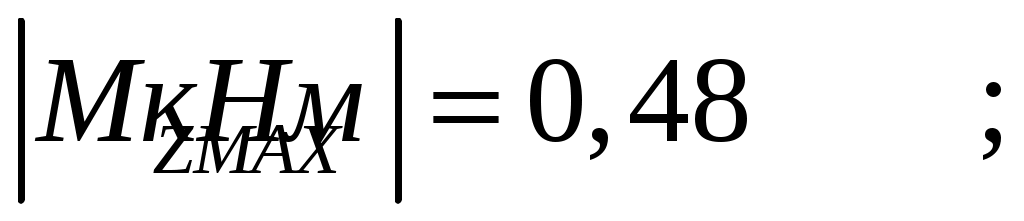
Подбираем двутавровую балку из условия прочности определив момент с противления сечения изгибу при заданном нормальным напряжении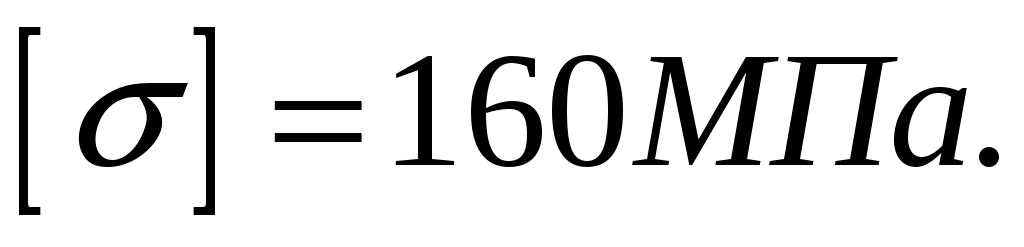
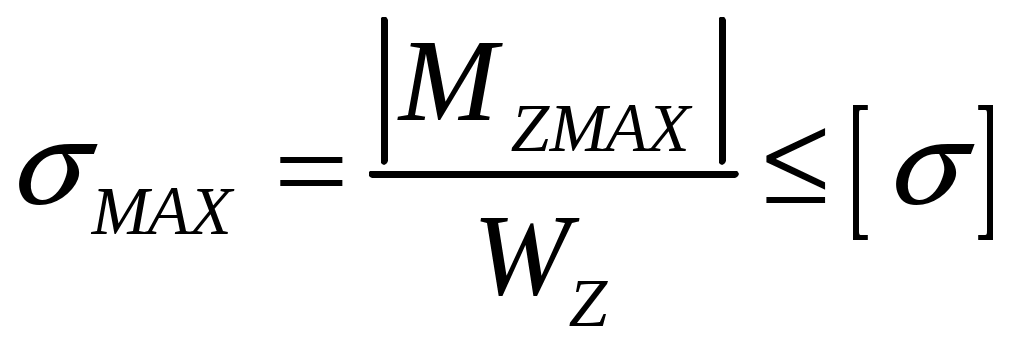 , откуда
, откуда 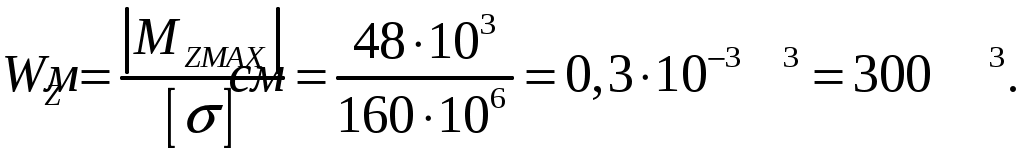
По ГОСТ8239-89 выбираем двутавр № 27 с ближайшим большим моментом сопротивлении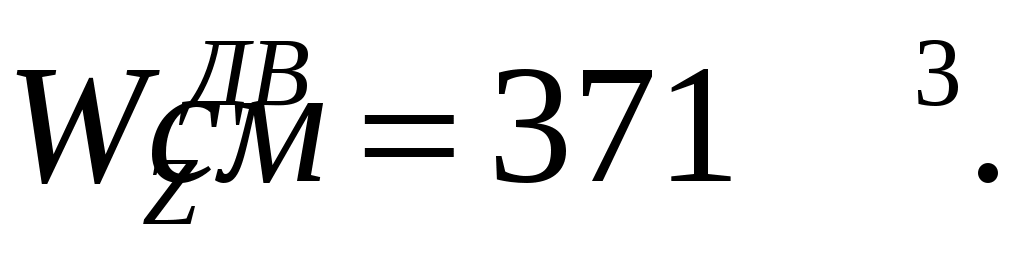
Вычислим абсолютное значение наибольшего нормального напряжения в опасных сечениях балки
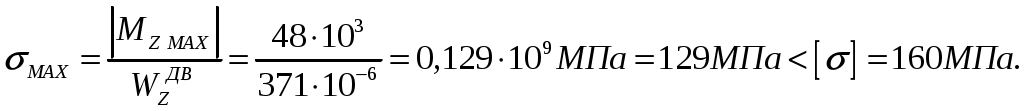
Условие прочности выполняется.
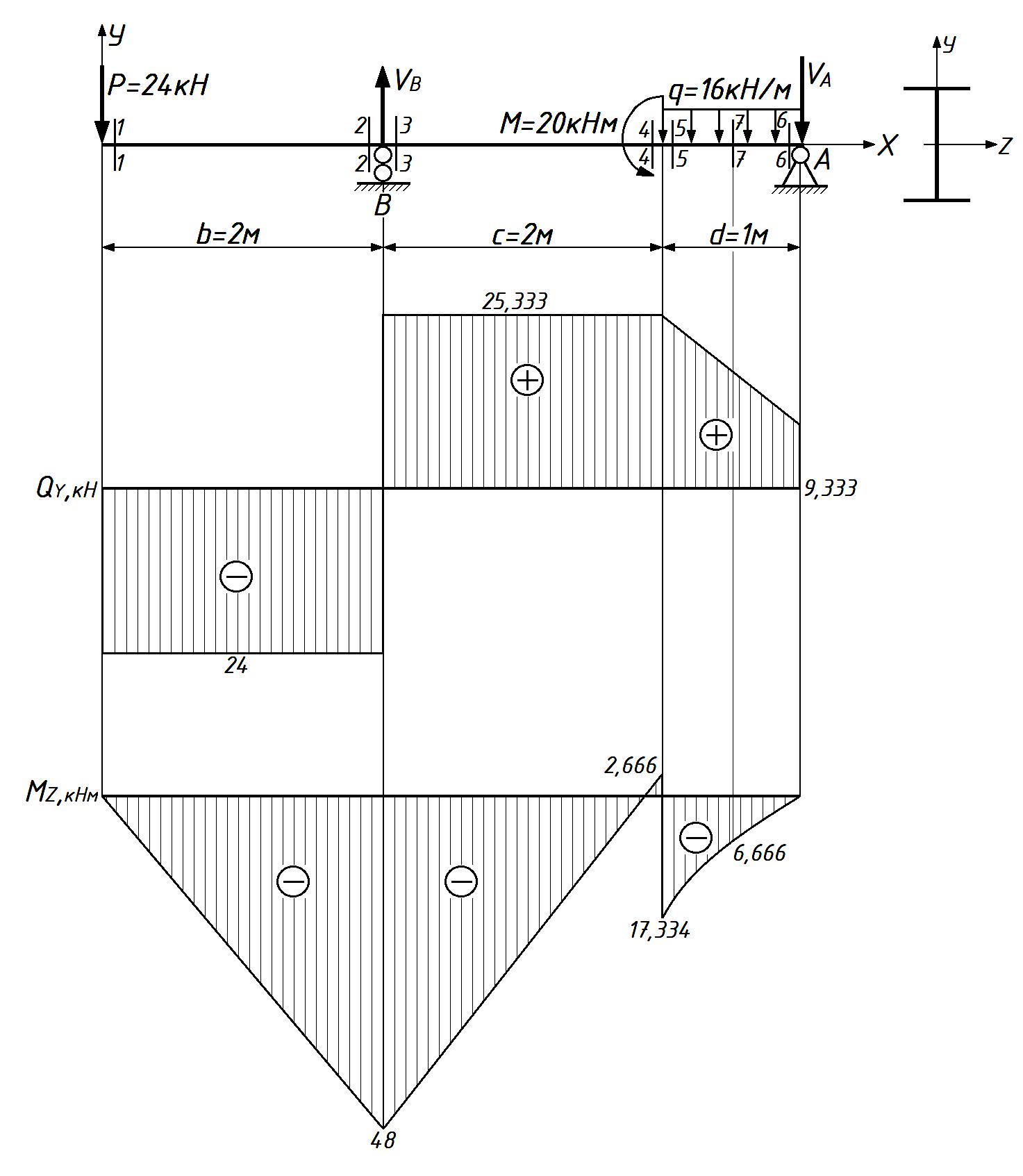
Рисунок 8. – Эпюры внутренних силовых факторов
Коэффициент запаса прочности по отношению к пределу текучести, если по условию задачи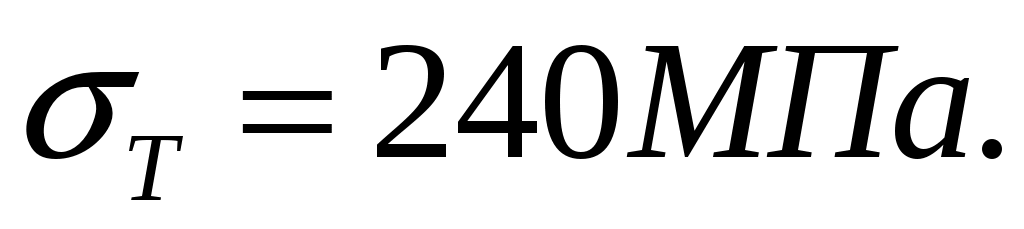
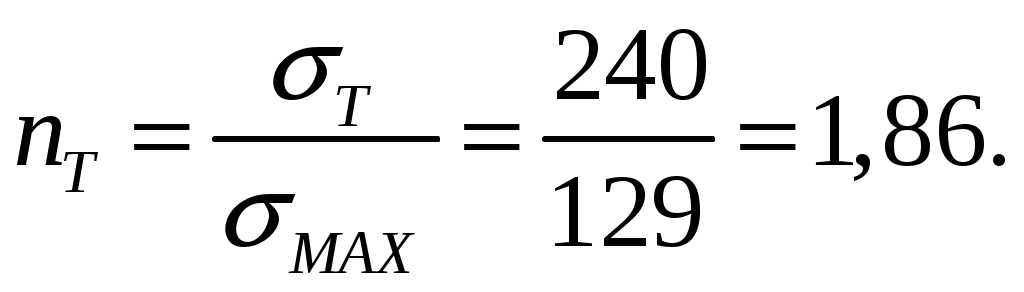
Величина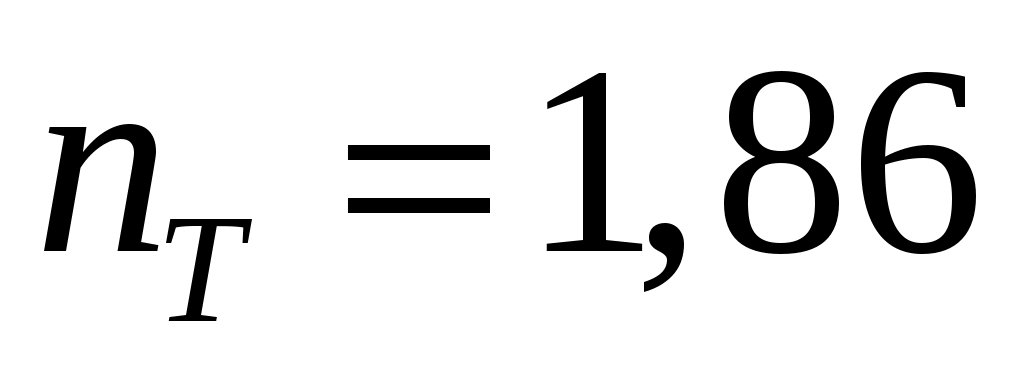 находится в рекомендуемом от 1,5 до 2,0диапазоне значений.
находится в рекомендуемом от 1,5 до 2,0диапазоне значений.
ЗАДАЧА № 4
КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Для заданного вала требуется:
Вычисленные диаметры округлить до ближайших больших целых значений.
Данные для расчета:
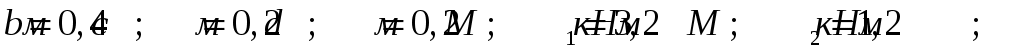
Решение:
Вал нагружен внешними скручивающими моментами, лежащими в плоскостях, перпендикулярных продольной оси вала.
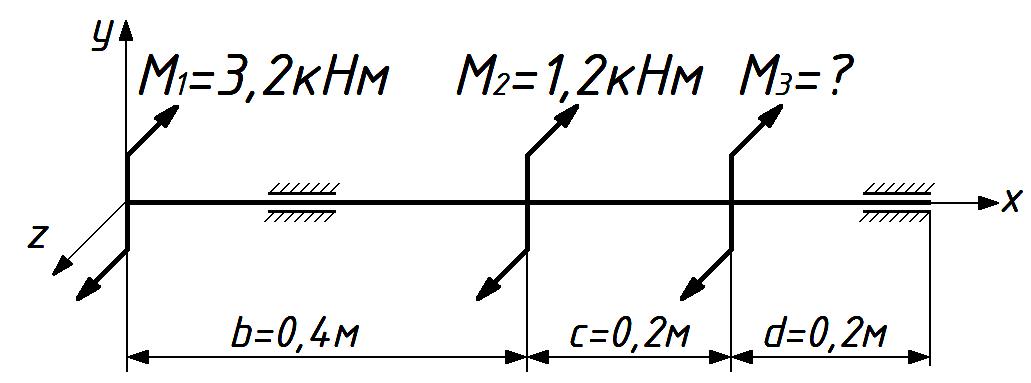
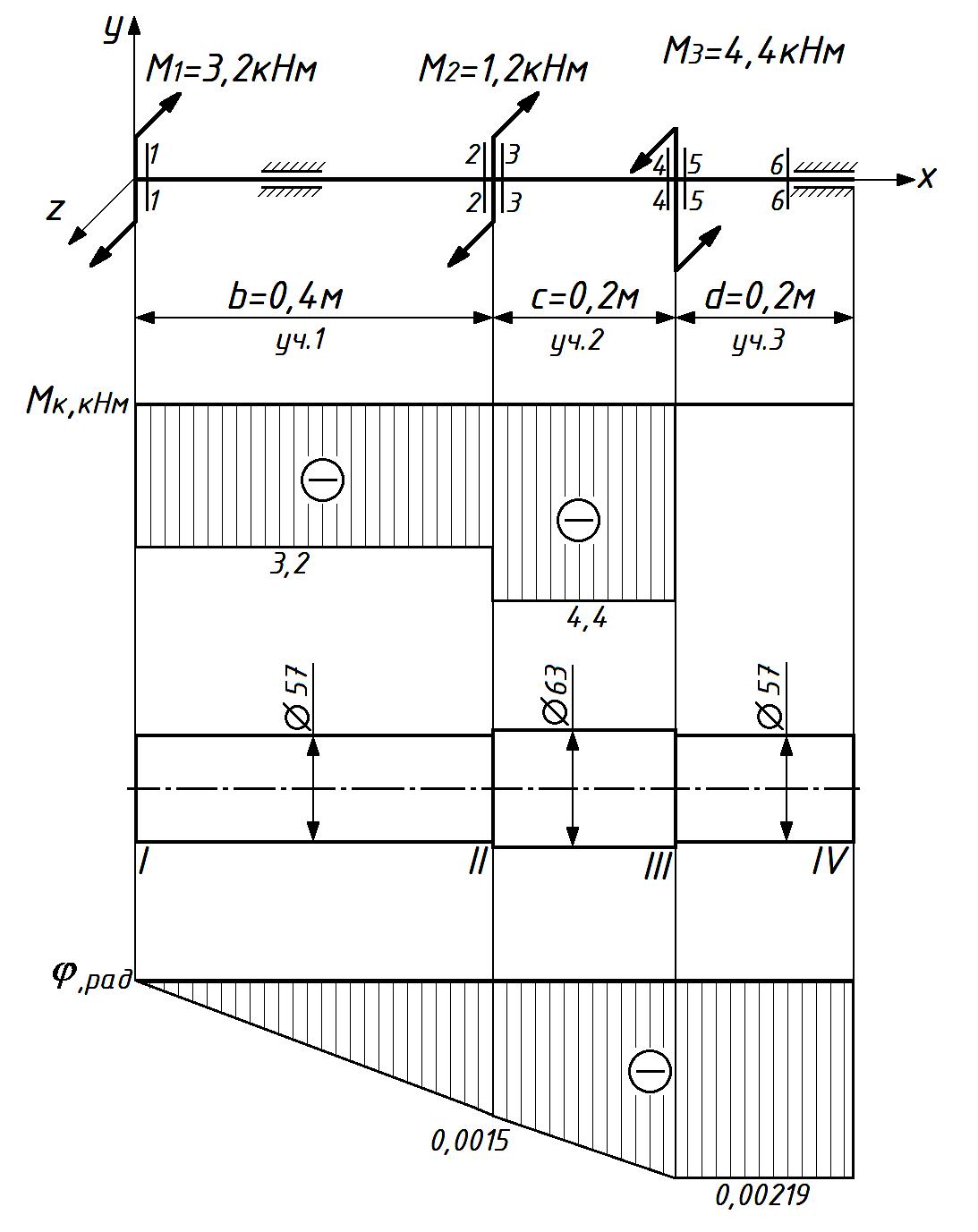
Рисунок 9. – Схема вала
Зададимся системой координат, в которой ось Х – продольна ось вала.
Составим уравнение равновесия относительно оси Х и найдем направление и величину неизвестного скручивающего момента М3:
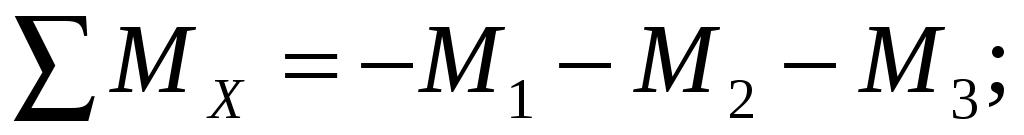
Знаки моментов одинаковы, так как направлены в одну сторону
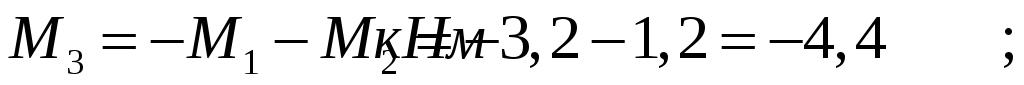
Знак (-) указывает на то, что действенное направление момента М3 противоположно ранее принятому
Вал имеет три участка, которые различаются характером нагружения.
Проведем в начале и в конце каждого участка характерные сечения и определим крутящие моменты в каждом сечении
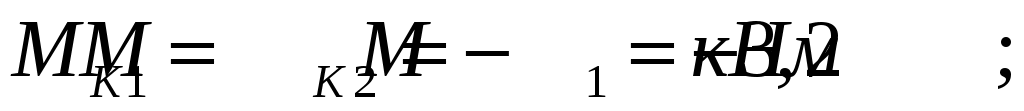
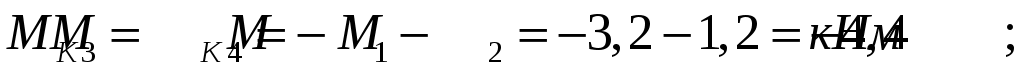
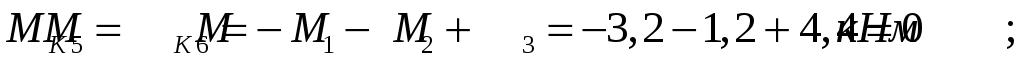
По полученным значениям строим эпюру крутящих моментов.
Из условия прочности по касательным напряжениям при кручении находим диаметр на каждом участке
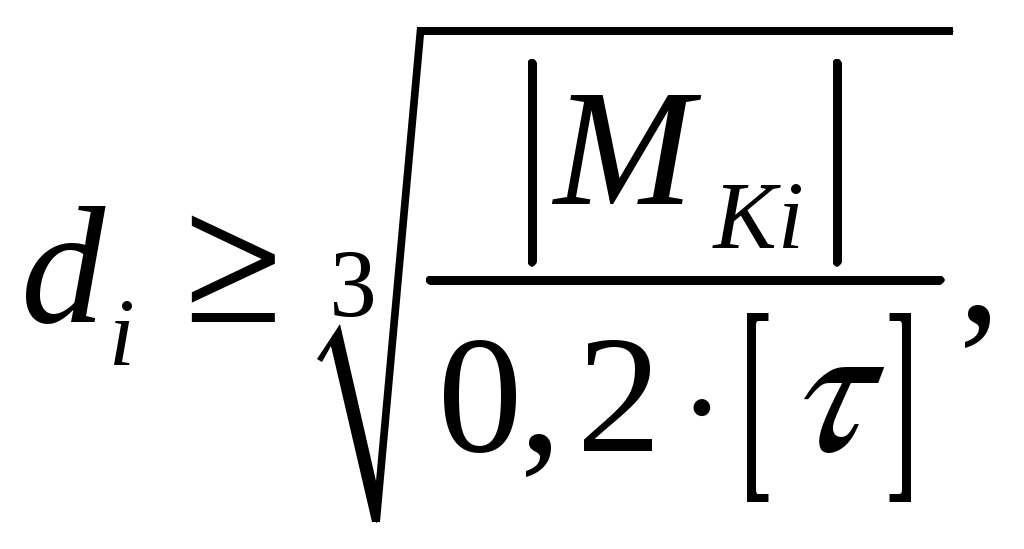
где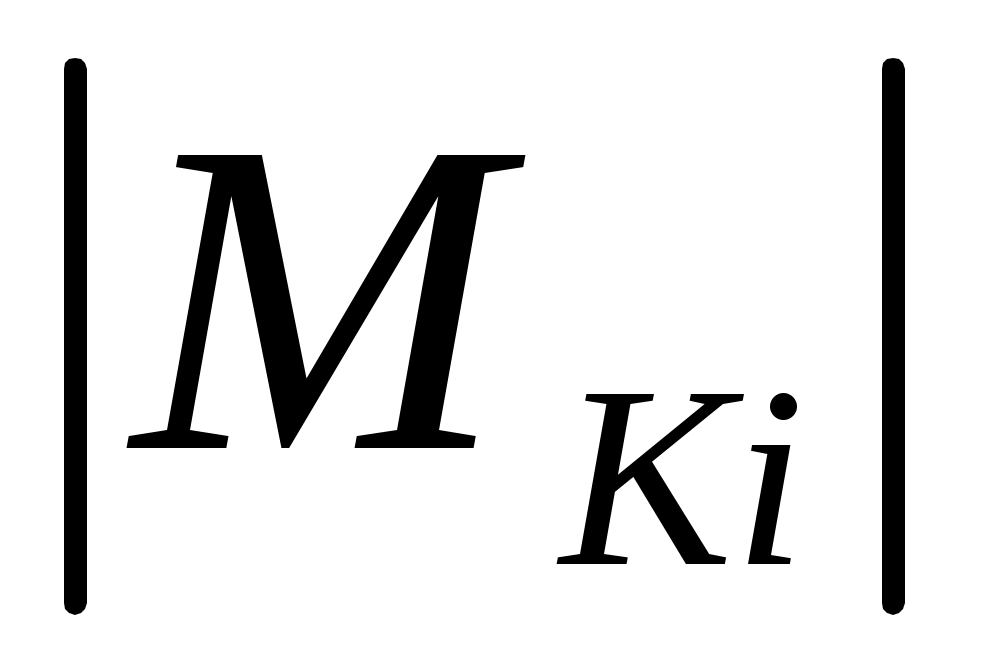 - абсолютное значение крутящего момента, действующего на i-ом участке вала, кНм;
- абсолютное значение крутящего момента, действующего на i-ом участке вала, кНм;
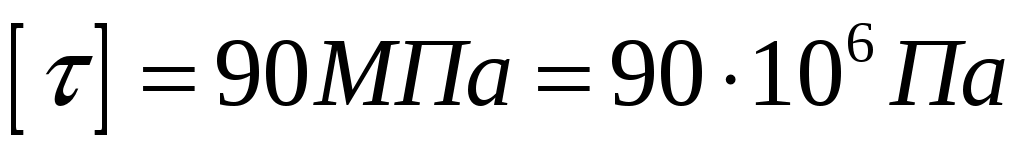 - допускаемое касательное напряжение;
- допускаемое касательное напряжение;
Диаметр вала на 1 участке;

Принимаем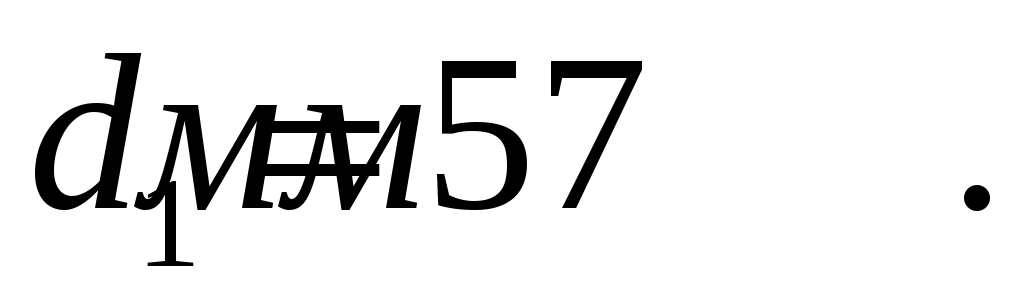
Диаметр вала на 2 участке;
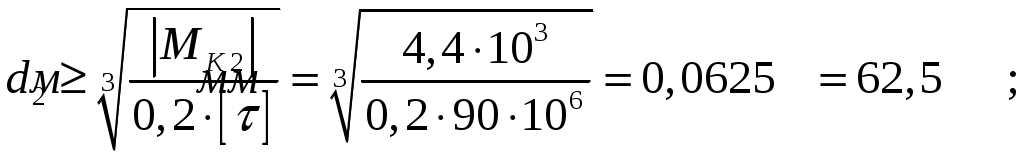
Принимаем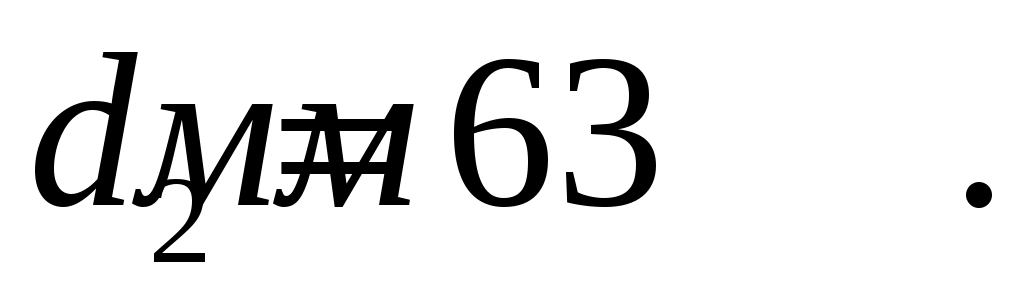
Диаметр третьего участка равен нулю. В этом случае принимаем диаметр равный наименьшему из принятых диаметр для других участков.
Принимаем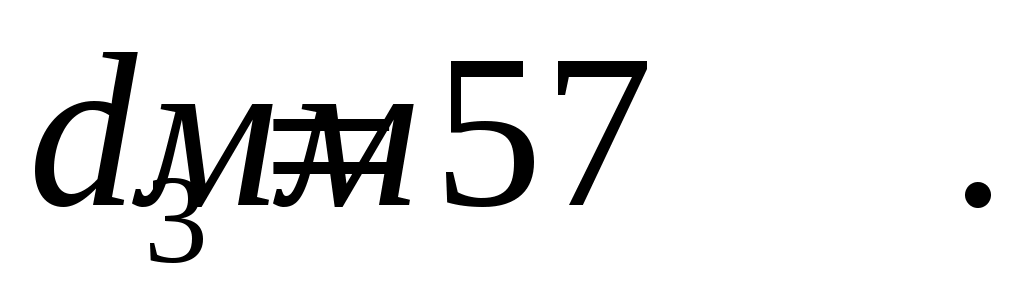
Определяем углы закручивания на участках вала:
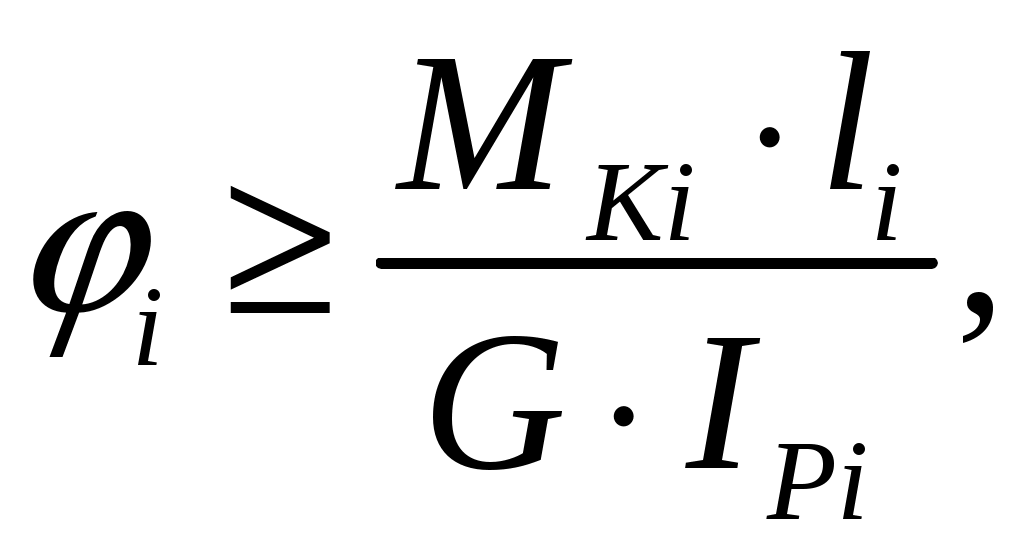
где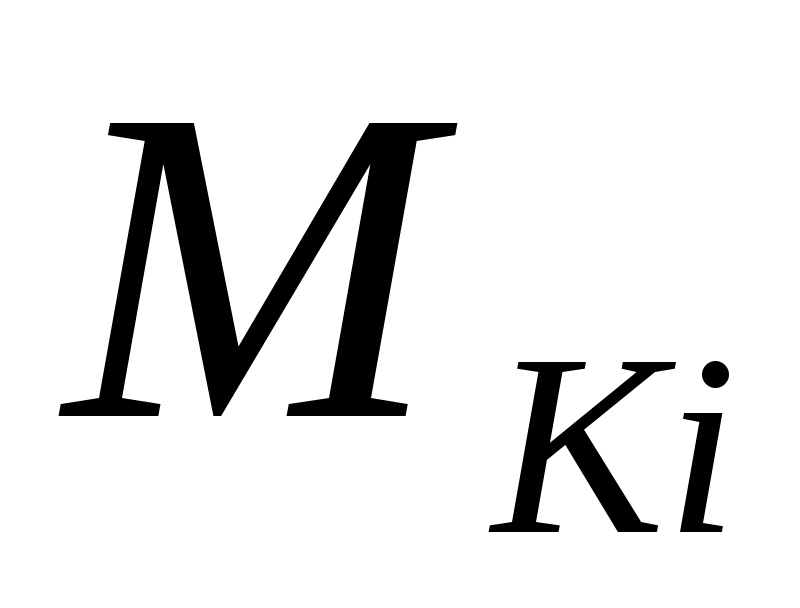 - крутящий момент, действующий на i-ом участке вала, Нм;
- крутящий момент, действующий на i-ом участке вала, Нм;
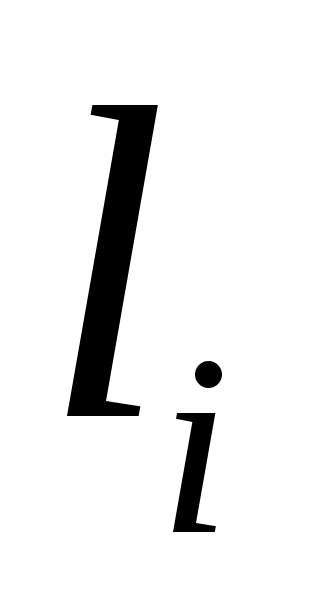 - длина i-го участка, м;
- длина i-го участка, м;
 - модуль сдвига, Па;
- модуль сдвига, Па;
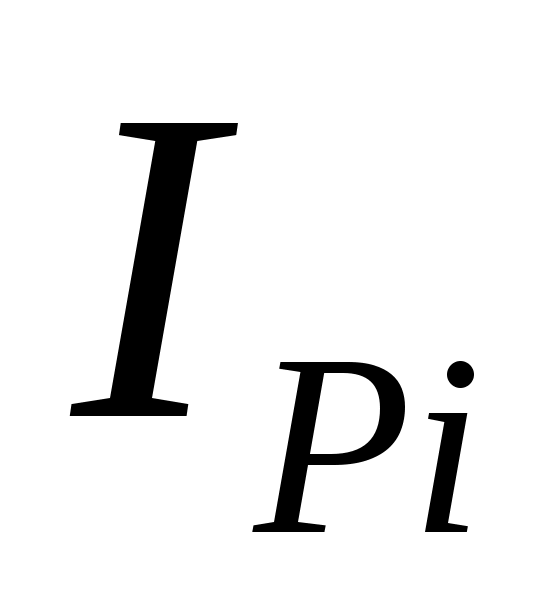 - полярный момент инерции сечения i-го участка, м4.
- полярный момент инерции сечения i-го участка, м4.
По эпюре крутящих моментов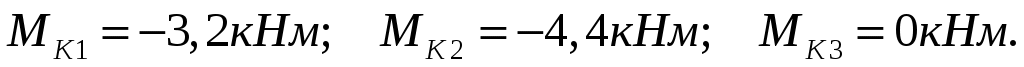
Вычислим полярные моменты инерции сечения вала на различных участках.
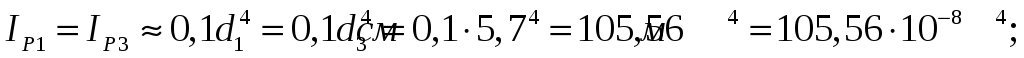
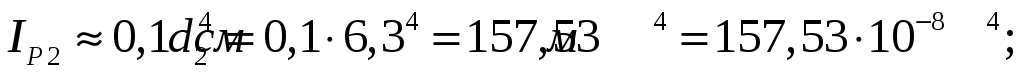
Определим углы закручивания участков вала:
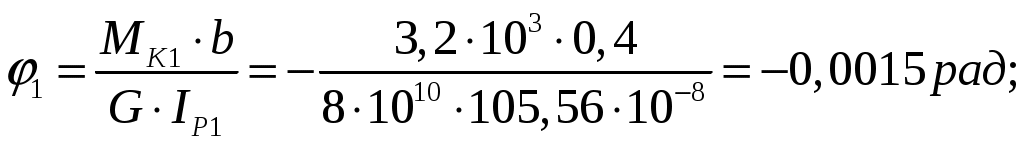
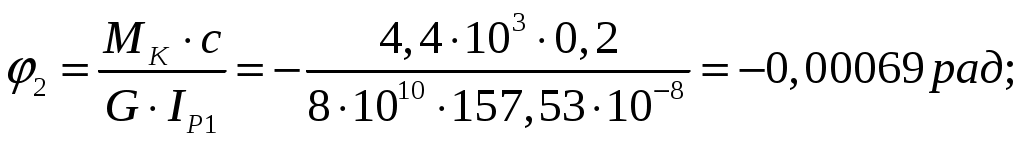
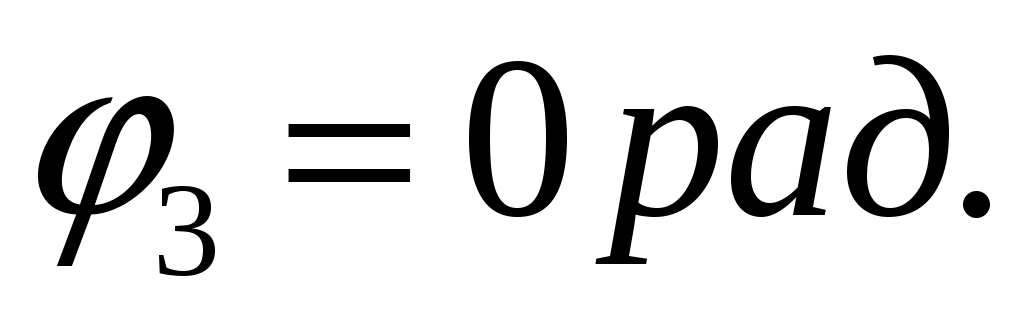
Сечения вала, совпадающие с границами участков, обозначим I, II, III, IV.
Для построения эпюры углов закручивания найдем углы поворота этих участков. Будем считать левое торцовое сечение вала неподвижным, то есть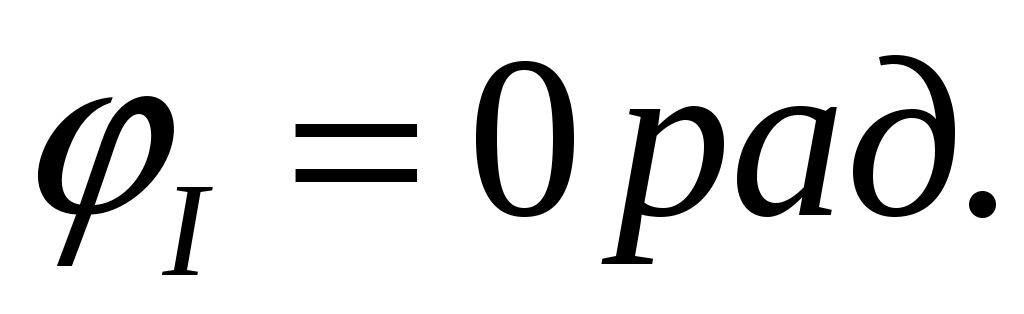
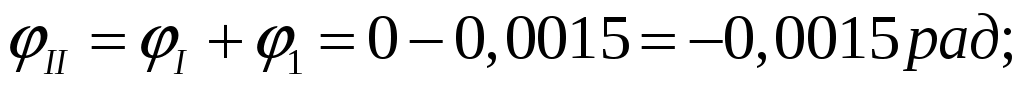
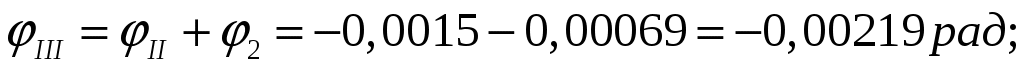
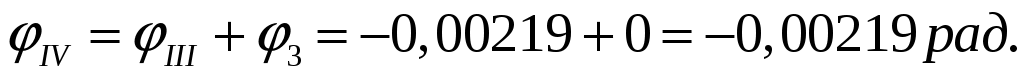
По данным значениям строим эпюру углов закручивания.
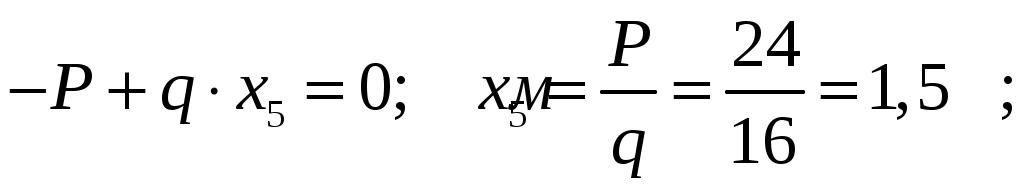
По вычисленным значениям строим эпюры внутренних усилий.

Рисунок 5 – Расчетная схема консольной балки и эпюры внутренних усилий
Условие прочности по нормальным напряжениям при прямом изгибе для балок из пластичных материалов имеет вид:
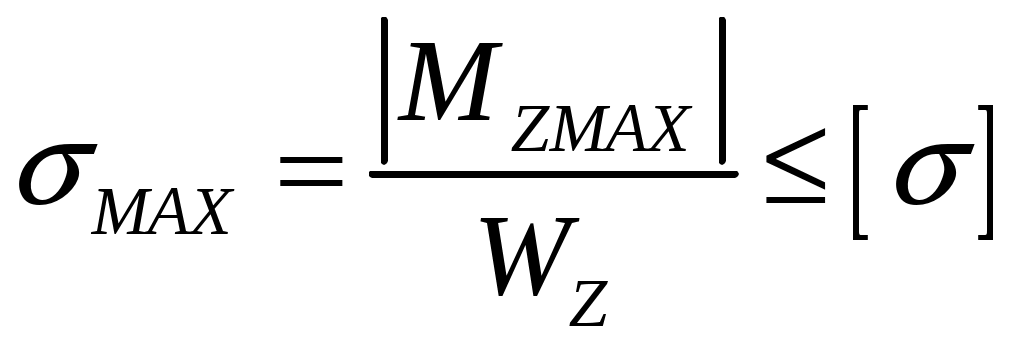 ,
,где
Определим абсолютное значение наибольшего нормального напряжения в опасном сечении балки и сравним его с допускаемым
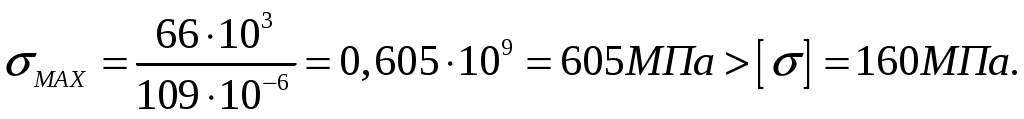
Условие прочности не выполняется. Необходимо принять двутавр не менее № 30, для которого
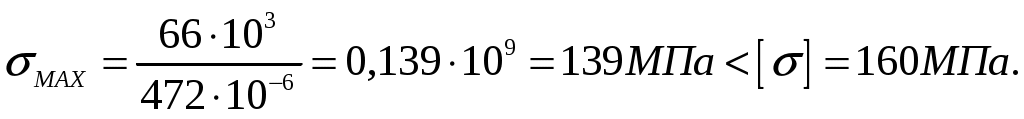
Расчет двух опорной балки
Двух опорная балка имеет три участка, различающихся характером нагружения, а следовательно, и законами изменения поперечных сил и изгибающих моментов.

Рисунок 6. – Схема двух опорной балки
Зададимся системой координат, совместив ось Х с продольной осью балки, а оси У и Z с главными центральными осями инерции поперечного сечения.
О
 пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют).
пределим опорные реакции. Отбросим опоры А и В и заменим их действие на балку вертикальными составляющими реакций VA и VB (горизонтальная составляющая в опоре А равна нулю, так как внешние горизонтальные нагрузки отсутствуют).Рисунок 7. – Расчетная схема двухопорной балки
Составим уравнения равновесия:
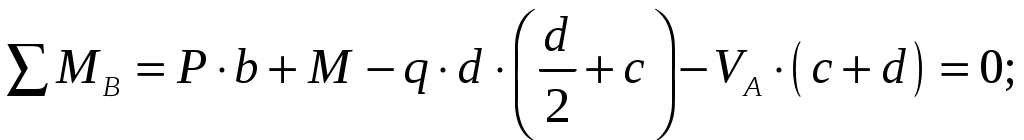
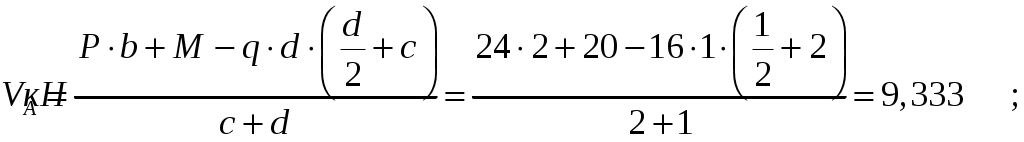
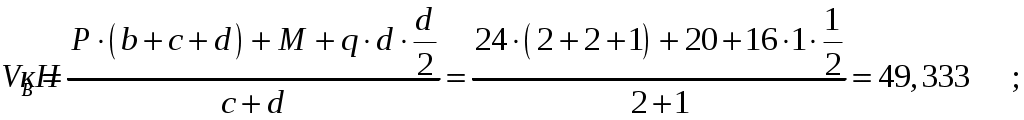
Для проверки правильности полученных результатов составим третье уравнение равновесия, спроецировав все силы на ось У:
Опорные реакции найдены верно.
Проведем характерные сечения и находим внутренние усилия в этих сечениях.
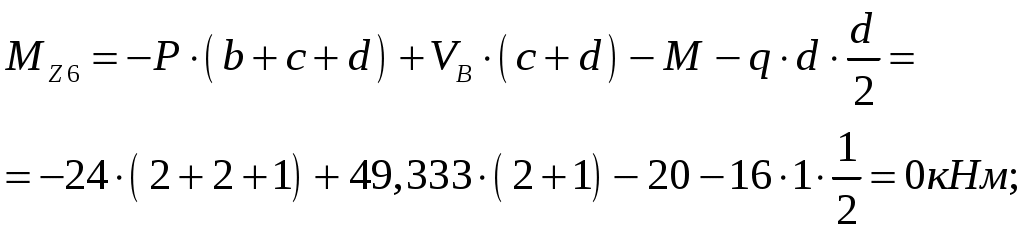
По вычисленным значениям построим эпюры внутренних усилий.
Опасными сечениями балки являются сечения 2-2 и 3-3.В них действует наибольший по абсолютному значению изгибающий момент
Подбираем двутавровую балку из условия прочности определив момент с противления сечения изгибу при заданном нормальным напряжении
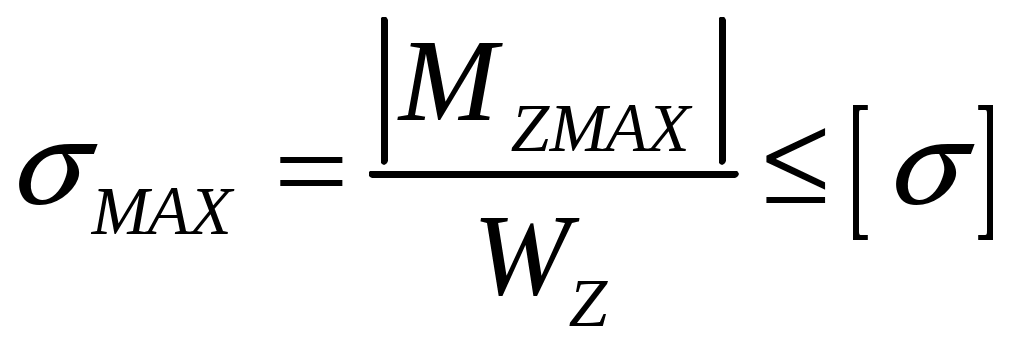 , откуда
, откуда 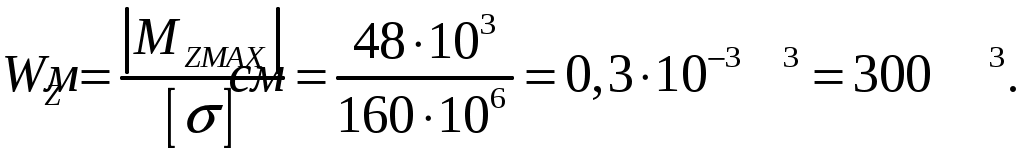
По ГОСТ8239-89 выбираем двутавр № 27 с ближайшим большим моментом сопротивлении
Вычислим абсолютное значение наибольшего нормального напряжения в опасных сечениях балки
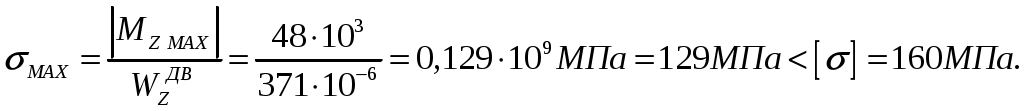
Условие прочности выполняется.

Рисунок 8. – Эпюры внутренних силовых факторов
Коэффициент запаса прочности по отношению к пределу текучести, если по условию задачи
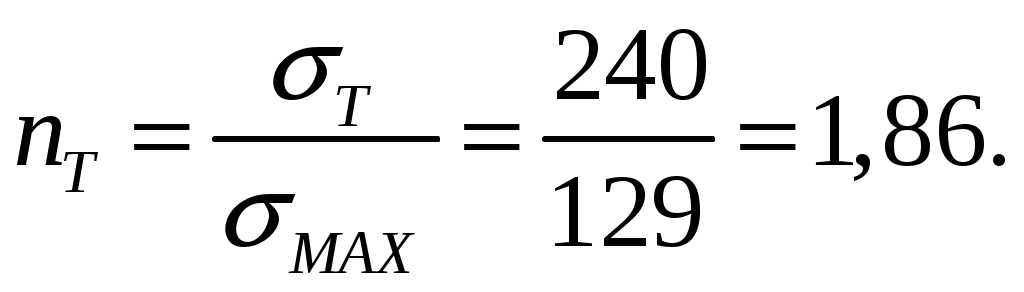
Величина
ЗАДАЧА № 4
КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Для заданного вала требуется:
-
Из условия равновесия определить направление и величину незаданного скручивающего момента. -
Построить эпюру крутящих моментов. -
Определит диаметр вала (материал – сталь Ст5) на каждом участке из условия прочности по касательным напряжениям, если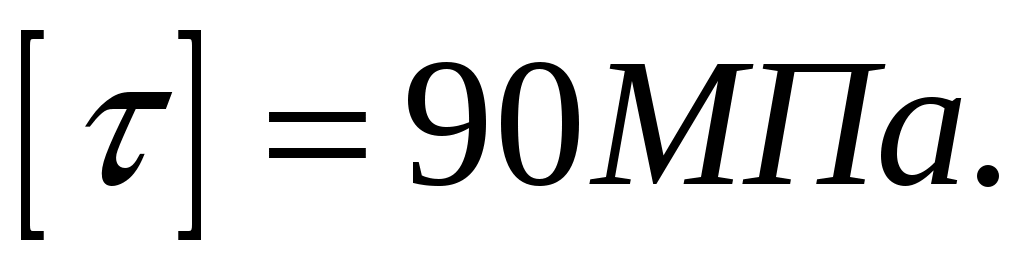
Вычисленные диаметры округлить до ближайших больших целых значений.
-
Построить эпюру углов закручивания (углов поворота) поперечных сечений вала, приняв за неподвижное левое торцовое сечение, если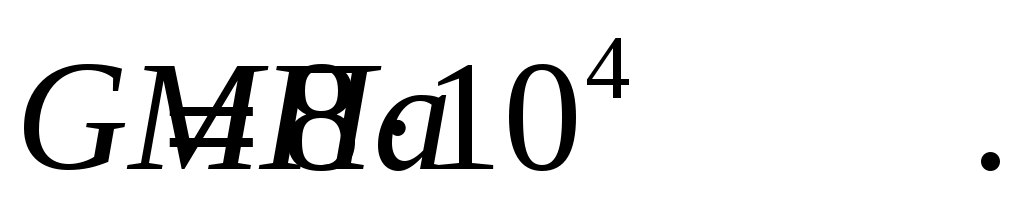
Данные для расчета:
Решение:
Вал нагружен внешними скручивающими моментами, лежащими в плоскостях, перпендикулярных продольной оси вала.

Рисунок 9. – Схема вала
Зададимся системой координат, в которой ось Х – продольна ось вала.
Составим уравнение равновесия относительно оси Х и найдем направление и величину неизвестного скручивающего момента М3:
Знаки моментов одинаковы, так как направлены в одну сторону
Знак (-) указывает на то, что действенное направление момента М3 противоположно ранее принятому
Вал имеет три участка, которые различаются характером нагружения.
Проведем в начале и в конце каждого участка характерные сечения и определим крутящие моменты в каждом сечении
По полученным значениям строим эпюру крутящих моментов.
Из условия прочности по касательным напряжениям при кручении находим диаметр на каждом участке
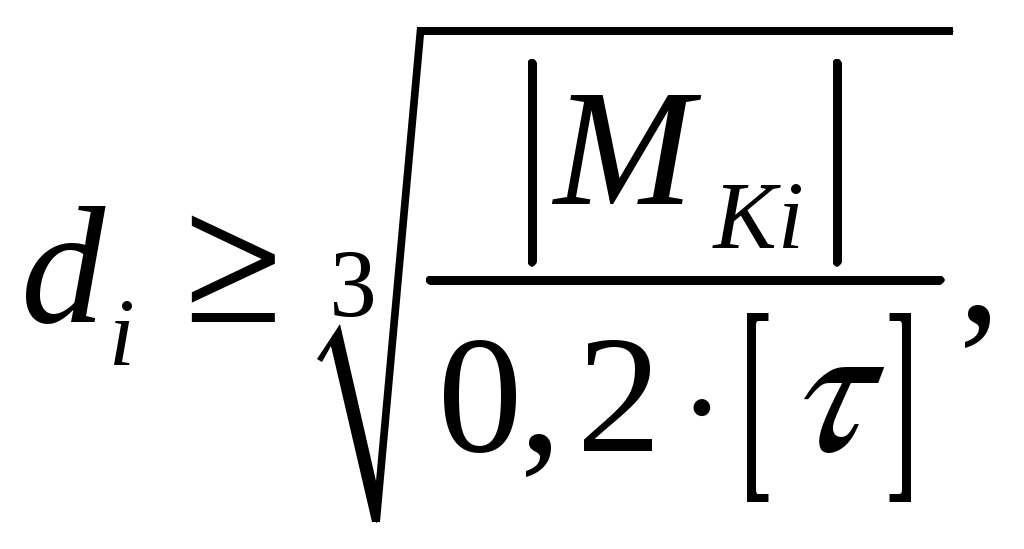
где
Диаметр вала на 1 участке;

Принимаем
Диаметр вала на 2 участке;
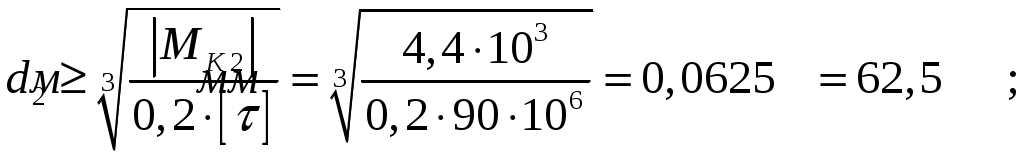
Принимаем
Диаметр третьего участка равен нулю. В этом случае принимаем диаметр равный наименьшему из принятых диаметр для других участков.
Принимаем
Определяем углы закручивания на участках вала:
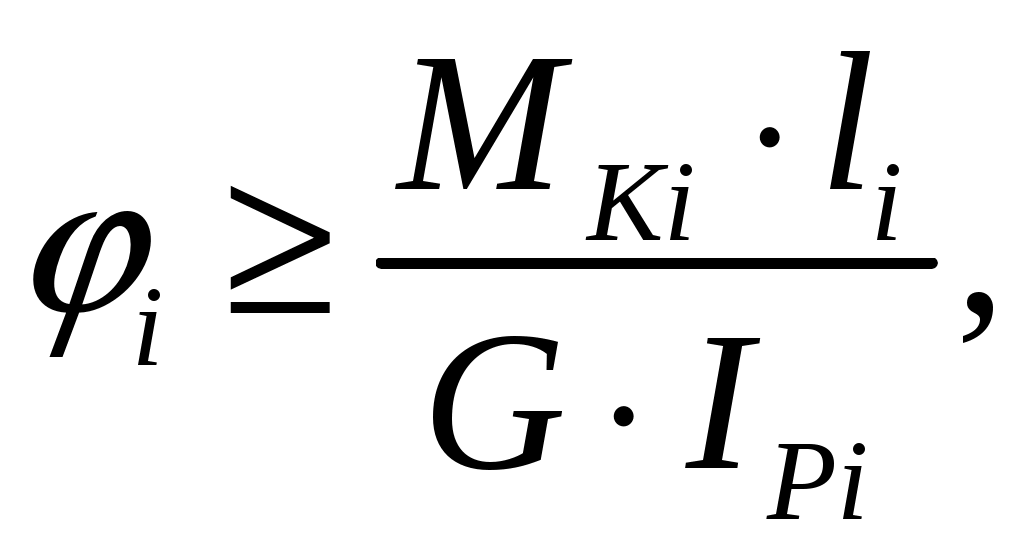
где
По эпюре крутящих моментов
Вычислим полярные моменты инерции сечения вала на различных участках.
Определим углы закручивания участков вала:
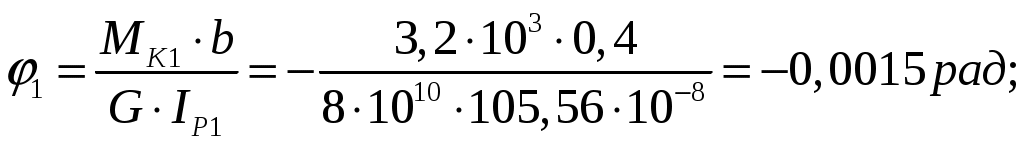
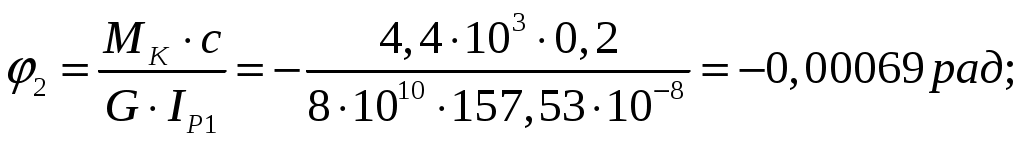
Сечения вала, совпадающие с границами участков, обозначим I, II, III, IV.
Для построения эпюры углов закручивания найдем углы поворота этих участков. Будем считать левое торцовое сечение вала неподвижным, то есть
По данным значениям строим эпюру углов закручивания.

