МИНОБРНАУКИ РОССИИ



Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Российский государственный гуманитарный университет»

(ФГБОУ ВО «РГГУ»)

ИНСТИТУТ ЭКОНОМИКИ, УПРАВЛЕНИЯ И ПРАВА

ФАКУЛЬТЕТ УРАВЛЕНИЯ

Строков Виктор Павлович

Основы математического моделирования социально-экономических процессов

Контрольная работа студента 3-го курса

заочной (с использованием дистанционных образовательных технологий) формы обучения группа ГМУ4-20

по дисциплине: «Математическое моделирование социально-экономических процессов»

Направление подготовки: Код 38.03.04 «Государственное и муниципальное управление»

Направленность (профиль): «Государственное и муниципальное управление»

Научный руководитель: Кононов Дмитрий Алексеевич

Москва 2023

Содержание



Задание 1

Экономическая система состоит из двух отраслей, для которых задана матрица прямых затрат А и вектор конечного продукта Y: , .

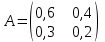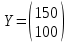Определить вектор валового выпуска Х, обеспечивающий заданный конечный продукт. Проверить продуктивность матрицы А.

Решение

1. Критерии продуктивности матрицы А:

Существует несколько критериев продуктивности матрицы А.

1. Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.

2. Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:

• 
  Определитель матрицы (E - A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E - A)^-1.
  
• 
  Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE - A| = 0 строго меньше единицы.
  
• 
  Все главные миноры матрицы (E - A) порядка от 1 до n, положительны.
  

---

Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности (при любом j сумма элементов столбца ∑a_ij ≤ 1.

2. Определим матрицу коэффициентов полных затрат B^-1 с помощью формул обращения невырожденных матриц.

Коэффициент полных затрат (b_ij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.

Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.

а) Находим матрицу (E-A):


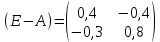
б) Вычисляем обратную матрицу (E-A)^-1:

Главный определитель



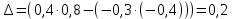
Определитель отличен от нуля, следовательно, матрица является невырожденной (продуктивной) и для нее можно найти обратную матрицу
B^-1.

Транспонированная матрица:



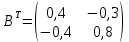
Найдем алгебраические дополнения матрицы B^T:









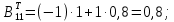
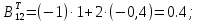
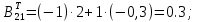
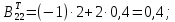
Обратная матрица:





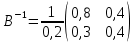
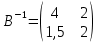
Таким образом, элементы каждого столбца b_ij показывают, сколько нужно затратить продукции каждой отрасли для производства только единицы конечного продукта j-й отрасли.

Найдем величины валовой продукции 2-х отраслей



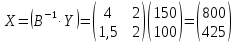
Ответ: вектор валового выпуска 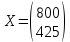; Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности.

Задание 2

Найти вектор 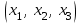национальных доходов трех стран в сбалансированной системе международной торговли, если сумма национальных доходов стран равна 5450 млн.$, а

---

структурная матрица торговли этих стран равна

.

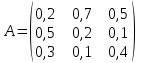Решение

Будем полагать, что 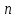стран ведут торговлю. Обозначим 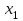, , 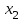…, 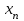части национальных бюджетов этих стран, которые расходуются на покупку товаров. Эти величины называют национальными торговыми бюджетами.

Пусть 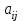– доля бюджета 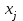, которую 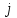-я страна тратит на закупку товаров у 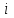-ой страны. Введем матрицу коэффициентов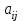

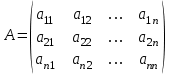. (1)

Так как национальный торговый бюджет расходуется только на закупки товаров внутри страны и вне ее, то справедливы равенства

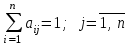. (2)

Матрицу 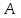вида (1) со свойством (2) называют структурной матрицей торговли.

Для 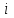-й страны общая выручка от внутренней и внешней торговли выражается формулой

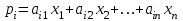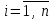, . (3)

Условие сбалансированной (бездефицитной) торговли заключается в том, что выручка от торговли каждой страны должна быть не меньше ее национального дохода, то есть 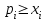или с учетом (3)

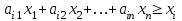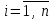, . (4)

Нетрудно показать, что в условиях (4) возможен только знак равенства. Действительно, сложим все эти неравенства при

---

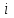от 1 до 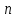. Группируя слагаемые с величинами бюджетов 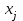, получим

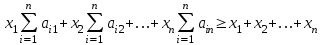. (5)

В силу условий (2) неравенство (5) можно записать так:

,

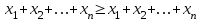откуда возможен только знак равенства.

Таким образом, условия (5) принимают вид

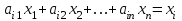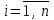, . (6)

Введем в рассмотрение вектор-столбец национальных торговых бюджетов 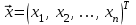, тогда уравнения (6) можно записать в матричной форме

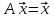. (7)

Это уравнение означает, что собственный вектор структурной матрицы торговли 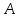, соответствующий ее собственному значению 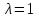, состоит из национальных торговых бюджетов стран, удовлетворяющих условию бездефицитной международной торговли.
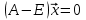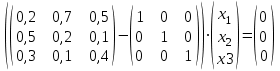Перепишем уравнение (7) в виде или

или .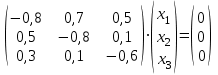
Перепишем матричное уравнение в виде системы


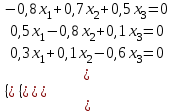
Выпишем основную матрицу системы:

-0,8 0,7 0,5 0,5 -0,8 0,1 0,3 0,1 -0,6 x1 x2 x3

---

Приведем матрицу к треугольному виду.
Умножим 1-ую строку на (0,63). Добавим 2-ую строку к 1-ой:

0 -0,36 0,41 0,5 -0,8 0,1 0,3 0,1 -0,6

Умножим 2-ую строку на (-0,6). Добавим 3-ую строку к 2-ой:

0 -0,36 0,41 0 0,58 -0,66 0,3 0,1 -0,6

Умножим 1-ую строку на (1,6). Добавим 2-ую строку к 1-ой:

0 0 0 0 0,58 -0,66 0,3 0,1 -0,6

В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.

0 0,58 -0,66 0,3 0,1 -0,6

---

Смотрите также файлы

• Пояснительная записка Программа внеурочной деятельности Мой край!.docx

• Религиозные учреждения в Тире назывались марзех.docx

• Виды изобразительного искусства (подготовка презентации).docx

• Общие проблемы малой группы. Динамические процессы в малой группе.docx

• Министерство просвещения росси.docx