ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 23
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Найдем ранг матрицы.
|
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно, rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1, x2, значит, неизвестные x1, x2 – зависимые (базисные), а x3 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
|
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
0,58x2 = 0,66x3
0,3x1 + 0,1x2 = 0,6x3
Получили соотношения, выражающие зависимые переменные
x1,x2 через свободные x3, то есть нашли общее решение:
x2 = 1,14x3
x1 = 1,62x3
Тогда
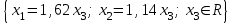 , и вектор национальных торговых бюджетов двух стран имеет вид
, и вектор национальных торговых бюджетов двух стран имеет вид 
, то есть бюджеты торгующих стран относятся как
 .
.Так как сумма национальных торговых бюджетов составляет
5450 млн. $, то есть
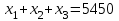 , или
, или 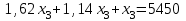 , тогда
, тогда 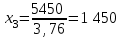 млн. $, а
млн. $, а  млн. $,
млн. $,  млн. $.
млн. $. Ответ: вектор национальных доходов трех стран:
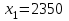 млн. $,
млн. $, 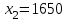 млн. $,
млн. $,  млн. $.
млн. $.Задание 3
Методом множителей Лагранжа решить задачу потребительского выбора, то есть найти точку спроса при условии, что доход потребителя составляет 12 000 ден. ед., цена первого товара – 25 ден. ед., цена второго товара – 5 ден. ед. Функция полезности потребителя для набора из двух товаров задана в виде
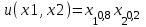 .
.Решение:
Для двух товаров целевая функция потребления имеет вид:
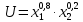
Вектор цен равен Р = (25; 5); величина дохода равна 1200.
Дифференцируя данную функцию полезности, получаем:
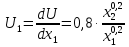

Необходимые условия оптимума дают следующую систему уравнений (λ – множитель Лагранжа):
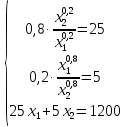
После подстановки первого уравнения во второе получим:
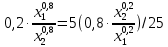
Выразив из третьего уравнения
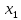 и подставив в последнее равенство, будем иметь:
и подставив в последнее равенство, будем иметь: 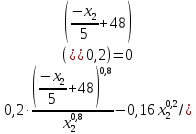
Решая его относительно
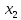 получим:
получим: 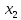 = 48
= 48Тогда рри
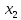 = 48, получим
= 48, получим 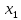 = 38,4;
= 38,4; = 40,1526.
= 40,1526.Ответ:
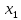 = 38,4;
= 38,4; 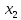 = 48;
= 48;  = 40,1526
= 40,1526Задание 4
Пекарня выпекает сегодня хлеб для продажи его магазинам завтра. Затраты на выпекание одного батона составляют 3 руб., а продают батон магазинам за 6 руб.
Спрос на хлеб завтра пекарне не известен, но по данным о спросе за последние периоды спрос на хлеб может составить: 0 батонов, 10 батонов, 20 батонов или 30 батонов.
1) Составить платежную матрицу пекарни, отражающую прибыль и убытки пекарни от продажи хлеба.
2) Составьте матрицу рисков.
3) Каким будет оптимальное решение пекарни, т.е. сколько батонов хлеба ей производить (10, 20 или 30), если спрос на хлеб завтра ему не известен и он использует для принятия решения:
а) критерий Лапласа;
б) максиминный критерий Вальда;
в) максимаксный критерий;
г) критерий максимаксного риска Сэвиджа.
4) Каким будет оптимальное решение пекарни при известных вероятностях спроса на хлеб завтра: отсутствие спроса 0,1, спрос на 10 батонов 0,3, спрос на 20 батонов 0,4 и спрос на 35 батонов 0,2, если пекарня использует критерий минимального ожидаемого риска?
Решение:
Каждая реализованная в течение дня единица приносит доход
6-3=3 рублей, а каждая нереализованная единица приносит убыток 6-3=3 рублей.
Исходя из этого, составим платежную матрицу:
| Возможные исходы: число проданных в день | Возможные решения: число для реализации единиц | |||
| 0 | 10 | 20 | 30 | |
| 0 | 0  3=0 3=0 | 0  3-10 3-10 3=-30 3=-30 | 0  3-20 3-20 3=-60 3=-60 | 0  3-30 3-30 3=-90 3=-90 |
| 10 | 0  3=0 3=0 | 10  3=30 3=30 | 10  3-10 3-10 3=0 3=0 | 10  3-20 3-20 3=-30 3=-30 |
| 20 | 0  3=0 3=0 | 10  3=30 3=30 | 20  3=60 3=60 | 20  3-10 3-10 3=30 3=30 |
| 30 | 0  3=0 3=0 | 10  3=30 3=30 | 20  3=60 3=60 | 30  3=90 3=90 |
Преобразовав ее, получим:
| Возможные исходы: спрос в день | Возможные решения: число для реализации единиц | |||
| 0 | 10 | 20 | 30 | |
| 0 | 0 | -30 | -60 | -90 |
| 10 | 0 | 30 | 0 | -30 |
| 20 | 0 | 30 | 60 | 30 |
| 30 | 0 | 30 | 60 | 90 |
Исходные данные:
| 0 | -30 | -60 | -90 |
| 0 | 30 | 3 | -30 |
| 0 | 30 | 60 | 30 |
| 0 | 30 | 60 | 90 |
Критерий Лапласа.
Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.:
q1 = q2 = ... = qn = 1/n.
qi = 1/4
| Ai | П1 | П2 | П3 | П4 | ∑(aij) |
| A1 | 0 | -7.5 | -15 | -22.5 | -45 |
| A2 | 0 | 7.5 | 0.75 | -7.5 | 0.75 |
| A3 | 0 | 7.5 | 15 | 7.5 | 30 |
| A4 | 0 | 7.5 | 15 | 22.5 | 45 |
| pj | 0.25 | 0.25 | 0.25 | 0.25 | |


