ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.07.2024
Просмотров: 408
Скачиваний: 3
СОДЕРЖАНИЕ
Глава 2. Первичные преобразователи
Глава 3. Усилители и стабилизаторы
Глава 4. Переключающие устройства и распределители
Глава 5. Задающие и исполнительные устройства
Глава 6. Общие сведения об измерении и контроле
Глава 8. Контроль давления и разрежения
Глава 9. Контроль расхода, количества и уровня
Глава 12. Автоматическая блокировка и защита в системах управления
Глава 13. Системы автоматического контроля и сигнализации
Глава 14. Системы автоматического
Глава 15. Объекты регулирования и их свойства
Глава 17. Конструкции и характеристики регуляторов
Глава 18. Общая характеристика
Глава 19. Математическое и программное обеспечение микроЭвм
Глава 20. Внешние устройства микроЭвм
Глава 21. Применение микропроцессорных систем
Глава 23. Конструкции промышленных роботов
Глава 25. Роботизация промышленного производства
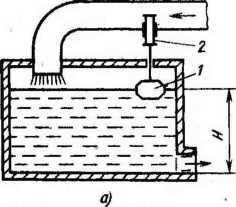
Рис. 120. Схема стабилизации температуры в термостате
Рис.
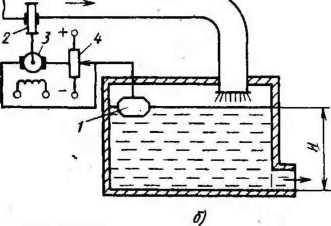
121. Схемы стабилизирующих регуляторов:
а
■— статического; б ~ астатического
 Во
второй схеме (рис. 121, б) поплавок 1
механически связан с ползуном реостата
4,
управляющего двигателем постоянного
тока 3.
При смещении ползуна реостата вверх
или вниз от среднего значения двигатель
перемещает задвижку 2
до тех пор, пока не восстановится заданный
уровень воды Я в баке, т. е. пока напряжение,
под&ваемое на двигатель, не станет
равным нулю.
Во
второй схеме (рис. 121, б) поплавок 1
механически связан с ползуном реостата
4,
управляющего двигателем постоянного
тока 3.
При смещении ползуна реостата вверх
или вниз от среднего значения двигатель
перемещает задвижку 2
до тех пор, пока не восстановится заданный
уровень воды Я в баке, т. е. пока напряжение,
под&ваемое на двигатель, не станет
равным нулю.
Следовательно, под астатическим регулированием понимается такое регулирование, которое поддерживает постоянное значение регулируемой величины при различных внешних возмущениях.
Программная система автоматического регулирования практически представляет собой стабилизирующую систему, в которой непрерывно изменяется задающее воздействие. Для получения определенной программы в таких системах предусмотрено специальное устройство, изменяющее заданное значение регулируемой величины в определенном направлении. В качестве примера таких систем можно назвать систему программного регулирования температуры в термических печах при ступенчатом отжиге и т. п.
Следящие автоматические системы регулирования предназначены для изменения регулируемой величины по закону заранее неизвестной функции времени. В таких системах применяется следующая терминология: вместо термина «регулирование» используется термин «слежение», входная величина — ведущая величина, выходная величина—ведомая величина.
В литейных и термических цехах следящие системы автоматического регулирования встречаются наиболее часто при регулировании соотношения расхода газа и воздуха в топливных печах. В таких системах при изменении расхода газа (ведущая величина) необходимо пропорционально изменять расход воздуха (ведомая величина), чтобы отношение газ—воздух сохранялось постоянным. Такая система обеспечивает экономичность сжигания топлива и позволяет получить в рабочем пространстве печи атмосферу заданного состава.
3. САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ
РЕГУЛИРОВАНИЯ
К группе самонастраивающихся систем относятся системы экстремального регулирования, системы с самонастройкой параметров и самонастройкой структуры.
Задачей экстремального регулирования является поддержание одного или нескольких показателей процесса на наиболее высоком или наиболее низком уровне при непрерывном изменении различных возмущающих воздействий, влияющих на условия работы системы. Таким образом, задача экстремального регулирования возникает, когда характеристика установившегося состояния объекта регулирования имеет экстремум, который отвечает наиболее желательному режиму работы системы. Более того, применение экстремального регулирования имеет смысл только в том случае, если внешние и внутренние возмущения вызывают перемещение экстремальной точки.
Следовательно, в системе экстремального регулирования должно быть дополнительное устройство (автоматического поиска экстремума), которое бы непрерывно изменяло установку регулятора с таким расчетом, чтобы поддерживать регулируемую величину или другой показатель на наивысшем или наинизшем уровне в условиях непрерывного изменения возмущающих воздействий.
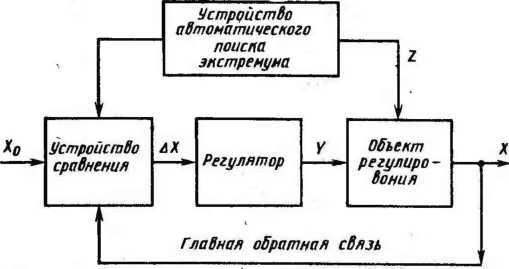
В экстремальной системе (рис. 122) имеются два замкнутых контура: один состоит из главной обратной связи, с помощью которой процесс регулирования осуществляется обычным способом; второй обеспечивает самонастройку системы, т. е. автоматический поиск оптимальной точки.
Примером такой системы является реализация задачи минимизации расхода топлива в двигателях самолета при полете на большие расстояния. Здесь минимум определяется в зависимости от расхода топлива на единицу пути и от скорости полета, причем положение этого минимума зависит от массы самолета, высоты полета, направления и скорости ветра и др.
Рис.
122. Схема системы экстремального
регулирования
В литейных и термических цехах эти системы пока не нашли широкого применения. В частности, их начинают использовать для регулирования процесса горения топлива в печах.
В системах с самонастройкой параметров при изменениях возмущающих воздействий или характеристик отдельных элементов автоматически корректируются те или иные параметры регулятора, например изменяются коэффициенты усиления, вводятся производная и интеграл в закон регулирования и т. п. В состав таких систем, как правило, входит вычислительное устройство, определяющее отклонение того или иного показателя работы системы от его оптимального значения, и настраивающее устройство, воздействующее на настройку параметров системы.
В качестве вычислительных устройств используют как аналоговые, так и цифровые ЭВМ.
Системы с самонастройкой структуры называют также самоорганизующимися системами. Они изменяют структурную схему основного управляющего устройства. Поэтому самонастраивающиеся системы этого вида относят к системам с переменной структурой.
Осуществляя автоматический поиск в соответствии с заданным критерием работы, система, самостоятельно используя вычислительные и логические устройства, выбирает из ряда заранее подготовленных структур наилучшую, оптимально отвечающую заданным условиям работы. Возможность изменения структуры расширяет область применения данных систем. Рассмотренный принцип используется в системах управления работами. *
-
качественные показатели АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
В соответствии с двумя основными режимами работы автоматических систем регулирования (установившимся и переходным) их показатели делят на две группы.
Основным параметром, характеризующим работу системы автоматического регулирования в установившемся режиме, является статическая ошибка. Статическая ошибка — остаточное отклонение регулируемой величины от заданного значения после окончания процесса регулирования. Она, например, может быть вызвана зоной нечувствительности первичного преобразователя.
Для уменьшения остаточной ошибки можно использовать принципы регулирования по возмущению в комбинированных системах автоматического регулирования. Из множества действующих возмущений выбирают главное, и в зависимости от его значения воздействуют на объект регулирования таким образом, 'чтобы скомпенсировать влияние данного возмущения на регулируемую величину.
При приложении к системе автоматического регулирования некоторого воздействия в ней начнется переходный процесс.
а) Б) 6)
Рис. 123. Простейшие аналоги систем с различной устойчивостью:
а — система устойчивости «в малом»; б — система неустойчивости; в — система устойчивости «в большом».
Если через некоторое время после прекращения воздействия в результате переходного процесса система вернется в установившееся состояние, то такая система называется устойчивой. Следовательно, устойчивость систем автоматического регулирования есть свойство системы возвращать регулируемую величину к заданному состоянию равновесия. Неустойчивая система не возвращается в равновесное состояние, из которого она по той или иной причине вышла, а непрерывно удаляется от него или совершает около него некоторые колебания.
В общем случае система автоматического регулирования может быть устойчивой только при малых возмущениях. Иллюстрацией устойчивости системы автоматического регулирования может служить шарик (рис. 123), помещенный в чаше. В этом примере координату центра тяжести шарика считают аналогом регулируемой величины. При малых отклонениях от дна шарик стремится занять положение на дне (рис. 123, а), При больших отклонениях он может перейти за края чаши, после чего он не сможет вернуться к своему положению равновесия на дне чаши. Неустойчивую систему можно иллюстрировать перевернутой чашей (рис. 123, б). Шарик, помещенный на ее вершине, при любом возмущении скатится вправо или влево и никогда не займет прежнего положения. Система (рис. 123, в) относится к устойчивой «в большом», поскольку шарик, находящийся во впадине, при любых отклонениях обязательно вернется в исходное положение.
В процессе регулирования в зависимости от свойств самого объекта и регулятора и правильности его настройки возможны различные типы переходных процессов. Апериодический процесс — процесс, характеризуемый тем, что после отклонения регулируемой величины X от заданного значения Хь она апериодически возвращается к новому устойчивому значению (рис. 124, а). Колебательный процесс с затухающей амплитудой — процесс, в котором регулируемая величина изменяется относительно заданного значения с затухающей амплитудой (рис. 124, б).
Рассмотренные процессы регулирования являются устойчивыми, т. е. после полученного возмущения процесс приходит к равновесию.
В неустойчивой системе регулируемая величина после возмущения и работы регулятора совершает гармонические колебания около заданного значения с постоянными амплитудой и частотой
Рис. 124. Кривые регулирования:
а — устойчивого апериодического процесса; б — неустойчивого процесса с затухающей амплитудой колебаний; в — устойчивого колебательного процесса; е — неустойчивого процесса о расходящейся амплитудой колебаний
а)
б)
РЛАААг
В)
—-чА
г)
Качество переходного процесса оценивается с помощью следующих параметров: длительности переходного процесса тцер, по истечении которого разность между заданным и текущим значениями регулируемой величины не превышает 5 %, и величины перерегулирования
а = (Хтах - Х0)/Х0, и.
где Х,ш,х и Х0 — максимальное и заданное значения регулируемой величины. Оптимальным считается, если а — 20 %, а число колебаний за время переходного процесса не превышает трех.
Существуют различные способы определения устойчивости системы: аналитический, экспериментальный и другие. оп
Аналитический способ заключается в решении уравнений, описывающих систему автоматического регулирования. Существуют три основных критерия устойчивости: критерий Рауса— Гурвица, критерий Михайлова и критерий Найквиста—Михайлова.
Критерий устойчивости Рауса—Гурвица позволяет судить об устойчивости системы по коэффициентам ее характеристического уравнения. Необходимым условием устойчивости систем автоматического регулирования является положительность всех коэффициентов характеристических уравнений этих систем.
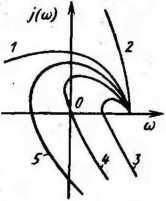
Рис. 125. Годографы замкнутых систем регулирования
Критерий устойчивости Михайлова — это
частотный критерий, основанный на построении по характеристическому уравнению системы характеристической кривой (или годографа), по виду которой судят по устойчивости систем автоматического регулирования.
Критерий Михайлова формулируется следующим образом: система устойчива, если годограф Михайлова / при изменении частоты © от 0 до +оо, начинаясь на положительной части вещественной полуоси, огибает против часовой стрелки начало координат, нигде не обращаясь в нуль, проходя последовательно такое количество квадрантов комплексной плоскости, какова степень Характеристического уравнения.

