Файл: Курсовая работа По дисциплине Теория многофазных течений.docx
Добавлен: 16.10.2024
Просмотров: 18
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Курсовая работа
По дисциплине: «Теория многофазных течений»
Содержание
1. Задача
Построить траекторию движения и найти зависимость изменения скорости от времени шара, брошенного под углом к горизонту.
При решении задачи учесть силу тяжести, силу Архимеда, силу трения и действие ветра. Направление скорости ветра совпадает с направлением оси ОХ.
Начальные условия для шара:


 м/c
м/c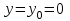
 м/c
м/c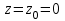
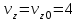 м/с
м/с
Данные для решения задачи:
-
диаметр шара: м
м -
плотность шара: кг/
кг/
-
плотность воздуха: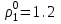 кг/м
кг/м
-
вязкость воздуха: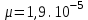 Па.с
Па.с
Коэффициент аэродинамического сопротивления шара принять равным:
 , Re=
, Re= ,
,где

 - векторы скорости ветра и шара.
- векторы скорости ветра и шара.| | Проекция скорости ветра на ось ОХ - 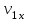 (м/c) (м/c) | Проекция скорости ветра на ось ОУ - 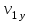 (м/c) (м/c) | Проекция скорости ветра на ось ОZ -  (м/c) (м/c) |
| | 2  | 0 | 0 |
2. Теоретическая часть
Фаза – это отдельная часть однофазной системы, ограниченная поверхностью раздела. Фаза может состоять из одного вещества и в таком случае она называется однокомпонентной. Если фаза состоит из нескольких химических веществ, то она называется многокомпонентной. Примером многокомпонентной фазы служит воздух. Движение тела под углом к горизонту
Рассмотрим классификацию сил, действующих со стороны несущей среды на дисперсную частицу:
В данной задаче для упрощения расчетов в качестве действующих сил учитываем только силу тяжести, силу Архимеда и силу трения.
-
Сила тяжести:

-
Сила Архимеда:
 сила Архимеда
сила Архимеда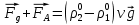
-
Сила трения:
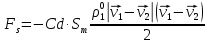 , где
, где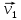 – вектор скорости несущей среды;
– вектор скорости несущей среды;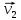 – вектор скорости частицы;
– вектор скорости частицы;  – коэффициент аэродинамического сопротивления;
– коэффициент аэродинамического сопротивления;  – площадь миделевого сечения частицы;
– площадь миделевого сечения частицы; Миделевое сечение – наибольшее по площади поперечное сечение тела, движущегося в воде или воздухе.
Если частица имеет сферическую форму, то на нее действует газовый поток
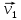 и в данном случае
и в данном случае  – площадь сферы.
– площадь сферы. ,
, 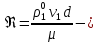 число Рейнольдса
число РейнольдсаЕсли
 ≈ 0÷1, то в этом случае реализуется ламинарный режим обтекания частицы несущей средой.
≈ 0÷1, то в этом случае реализуется ламинарный режим обтекания частицы несущей средой.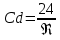
, сила трения
 – ламинарный или безотрывный режим течения.
– ламинарный или безотрывный режим течения.При переходном режиме течения
 ≈ 1÷700
≈ 1÷700При движении возникают вихревые зоны. За частицей возникают отрывные зоны.
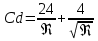
Турбулентный (автомодельный) режим течения:
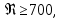 скорость газового потока очень велика. Возникают вихревые кольца. Коэффициент аэродинамического сопротивления находится по формуле:
скорость газового потока очень велика. Возникают вихревые кольца. Коэффициент аэродинамического сопротивления находится по формуле: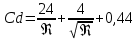
При построении графика зависимости коэффициента аэродинамического сопротивления
 от числа Рейнольдса
от числа Рейнольдса  выделяют Стоксовский режим, переходный режим, автомодельный режим, кризис сопротивления.
выделяют Стоксовский режим, переходный режим, автомодельный режим, кризис сопротивления.3. Решение задачи
На шар, брошенный под углом к горизонту, действуют сила тяжести, силу Архимеда, силу трения и действие ветра.
Тогда уравнение движение шара имеет следующий вид:


Что бы получили значения изменения скоростей движения шара и его координат, будем использовать численные методы. Методы Рунге – Кутта – это большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. Кутта.
К классу методов Рунге – Кутта относятся явный метод Эйлера и модифицированный метод Эйлера с пересчётом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализуется в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге – Кутта, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями.
Методы седьмого порядка должны иметь по меньшей мере девять стадий, а методы восьмого порядка – не менее 11 стадий. Для методов девятого и более высоких порядков (не имеющих, впрочем, большой практической значимости) неизвестно, сколько стадий необходимо для достижения соответствующего порядка точности.
Среди достоинств методов Рунге – Кутта, определивших их популярность, можно выделить следующее:
-
Эти методы легко программируются, -
Эти методы обладают достаточными для широкого круга задач свойствами точности и устойчивости. -
Эти методы (как и все одношаговые методы) являются самостартующими и позволяют на любом этапе вычислений легко изменять шаг интегрирования.
Классический метод Рунге – Кутта четвёртого порядка
Метод Рунге – Кутта четвёртого порядка при вычислениях с постоянным шагом интегрирования столь широко распространён, что его часто называют просто методом Рунге – Кутта.
Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка. Далее
 ;
; 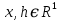 .
. .
.Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

Вычисление нового значения проходит в четыре стадии:

 ,
,
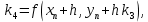
где
 – величина шага сетки по
– величина шага сетки по  .
.


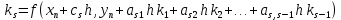
Конкретный метод определяется числом
 и коэффициентами
и коэффициентами 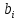 ,
,  и
и 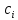 . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера).
. Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера).Этот метод имеет четвёртый порядок точности. Это значит, что ошибка на одном шаге имеет порядок O (
 ), а суммарная ошибка на конечном интервале интегрирования имеет порядок O (
), а суммарная ошибка на конечном интервале интегрирования имеет порядок O ( ).
). Явные методы Рунге – Кутта
Семейство явных методов Рунге – Кутта является обобщением как явного метода Эйлера, так и классического метода Рунге – Кутта четвёртого порядка. Оно задаётся формулами:
