М ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования

«Тольяттинский государственный университет»
Тольятинский государственный университет

(наименование института полностью)
Кафедра /департамент /центр¹ Машиностроение__________________________________

(наименование кафедры/департамента/центра полностью)

МСбп – 2004а

(код и наименование направления подготовки, специальности)

Современные технологические процессы изготовления деталей в машиностроении

(направленность (профиль) / специализация)


Практическое задание № 1_
по учебному курсу « Высшая Математика »

(наименование учебного курса)
Вариант ____ (при наличии)

Студент	Юнусов Альфред Эльмирович (И.О. Фамилия)
Группа	МСбп – 2004а (И.О. Фамилия)
Преподаватель	Кошелёва Наталья Николаевна (И.О. Фамилия)

Тольятти 2020

РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА

1.Номер варианта задачи определяется с помощью таблицы по первой букве фамилии студента (Ю)

Определить собственные значения и собственные векторы матрицы третьего порядка.

Вариант № 12

---

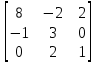
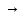
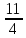
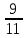= 8 = 18

2. Номер варианта задачи определяется с помощью таблицы по первой букве имени студента (А)

Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.

Вариант № 1






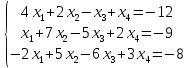
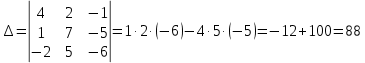
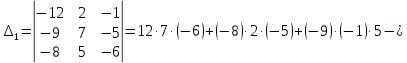
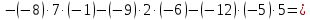
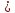504 + 80 + 45 – 56 – 108 – 300 = 165

+













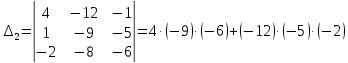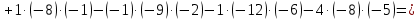
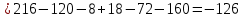
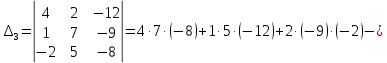
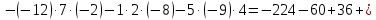
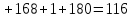
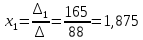
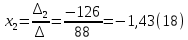
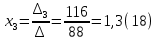
3.Номер варианта задачи определяется с помощью таблицы по первой букве отчества студента. (Э)

Исследовать и найти общее решение системы линейных однородных уравнений

Вариант № 19

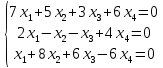
Матричный вид записи: Ax=b, где

A= 7 5 3 6 2 −1 −1 4 1 8 6 −6  , b= 0 0 0

---

Для решения системы, построим расширенную матрицу:

7 5 3 6 0 2 −1 −1 4 0 1 8 6 −6 0

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_1,1. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/7,-1/7 соответственно:

---

7 5 3 6 0 0 − 17 7 − 13 7 16 7 0 0 51 7 39 7 − 48 7 0

---

Исключим элементы 2-го столбца матрицы ниже элемента a_2,2. Для этого сложим строку 3 со строкой 2, умноженной на 3:

7 5 3 6 0 0 − 17 7 − 13 7 16 7 0 0 0 0 0 0

---

Смотрите также файлы

• Программа сезонной (летней) школы Центр весёлых ребят.docx

• Наименование норматива Условия выполнения норматива.docx

• Рубежный контроль 1 Форма рубежного контроля устный опрос.docx

• Здесь и ниже приведены рекомендации по заполнению шаблона Отчет о практике.doc

• Основы философии (часть 11) о22 Бондаренко.pdf