где x₃, x₄− произвольные действительные числа.

Сделаем следующие обозачения:

x3=λ1, x4=λ2.

Тогда

x1= 2 17 · λ1 − 26 17 · λ2
x2= − 13 17 · λ1 + 16 17 · λ2

---

x3=λ1,

x4=λ2.

где λ₁, λ₂− произвольные действительные числа.

Решение в векторном виде:

x= x1 x2 x3 x4 = 2 17 − 13 17 1 0 ·λ1 + − 26 17 16 17 0 1 ·λ2

---

λ₁, λ₂− произвольные действительные числа.

---

РАЗДЕЛ № 2. ВЕКТОРНАЯ АЛГЕБРА

1.Номер варианта задачи определяется с помощью таблицы по первой букве фамилии студента (Ю)

Составить уравнение плоскости Р, проходящей через точку А перпендикулярно вектору  BC . Написать ее общее уравнение, а также нормальное уравнение плоскости и уравнение плоскости в отрезках. Составить уравнение плоскости P1 , проходящей через точки А, В, С. Найти угол между плоскостями Р и P1 . Найти расстояние от точки D до плоскости Р.

Вариант № 12

А (0; -1; 2); В (-1; -1; 6); С (-2; 0; 2); D (0; 1; 4)



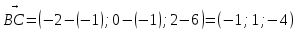
Уровнение плоскости Р, проходящей через точку А (-1;1;-4) и перпендикулярной вектору :



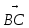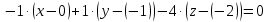
-x + 0 + y + 1 - 4z – 8 = 0

-x + y – 4z – 7= 0

Уравнение (нормальное)







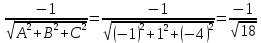
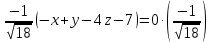
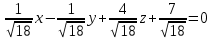
Уравнение в отрезках

-x + y – 4z =



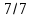
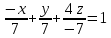
Уравнение плоскости : А(0;-1;-2); В(-1;-1;6); С(-2;0;2)









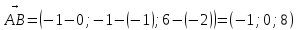
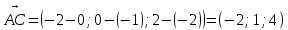
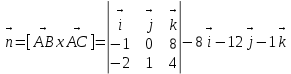
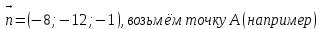
-8 (x-0) - 12 (y-(-1)) – 1 (z-(-2)) = 0

-8x -12y – 12 – z – 2 = 0

-8x – 12y – z – 14 = 0

Угол между плоскостями Р и

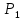
-x + y – 4z – 7 = 0 и -8x – 12y – z – 14 = 0





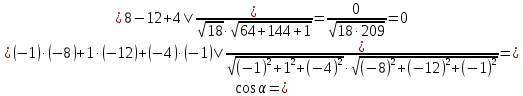
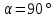
Расстояние от Д до плоскости Р

Д(0;1;4), -x + y – 4z – 7 = 0 в нормальном виде

---

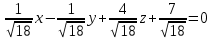
|ДН| =


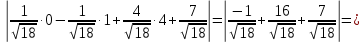
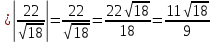
Уравнение в отрезках

2. Номер варианта задачи определяется с помощью таблицы по первой букве имени студента. (А)

Прямая l задана в пространстве общими уравнениями. Написать её каноническое и параметрическое уравнения. Составить уравнение прямой L , проходящей через точку М параллельно прямой L, и вычислить расстояние между ними. Найти проекцию точки М на прямую L и точку пересечения прямой L и плоскости Р.

Вариант № 1
Общее уравнение прямой L Координаты точки М Общее уравнение плоскости Р

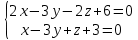(0;2;-1) x – 2y + 3z – 4 = 0
Прямая l задана как линия пересечения двух плоскостей:
{2x–3y–2z+6=0
{x–3y+z+3=0
Найдем две точки, принадлежащие линии пересечения.
Пусть первая координата точки, принадлежащей линии пересечения х=0
Тогда система принимает вид:
{–3y–2z+6=0
{–3y+z+3=0
Вычитаем из первого второе:
–3z+3=0
z=1
3y=z+3
y=4/3
А(0; 4/3; 1)
Пусть вторая координата точки, принадлежащей линии пересечения y=0
Тогда системa принимает вид:
{2x–2z+6=0
{x+z+3=0
умножаем второе на 2 и складываем
{2x–2z+6=0
{2x+2z+6=0
4х+12=0
х=–3
z=0
В(–3;0;0)
Cоставляем уравнение прямой. проходящей через две точки
А(0; 4/3; 1) и В(–3;0;0)


(x–0)/–3–0=(y+(4/3))/(0–(4/3))=(z–1)/(0–1)
x/(–3) =(y+(4/3))/(–4/3) =(z–1)/(–1) – каноническое уравнение
прямой l
Уравнение прямой l1 параллельной l есть уравнение прямой, проходящей через точку М (0;2;–1)
с таким направляющим вектором
s=(–3;4/3;–1)
x–0/(–3) =(y–2)/(–4/3) =(z+1)/(–1) – каноническое уравнение
прямой l1
Чтобы найти точку пересечния прямой l и плоскости Р.
Вводим параметр:
x/(–3) =(y+(4/3))/(–4/3) =(z–1)/(–1)=t
{x=–3t
{y=(–4/3)t–(4/3)
{z=–t+1
Подставляем в уравнение плоскости Р
(–3t)–2·((–4/3)t–(4/3))+3·(–t+1)–4=0
t=1/2
тогда
х=–3/2
y=–2
z=1/2
(–3/2;–2;1/2) – точка пересечения прямой l и пл. Р
РАЗДЕЛ № 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

1.Номер варианта задачи определяется с помощью таблицы по первой букве отчества студента (Э)

Даны координаты вершин треугольника АВС. Составить уравнения сторон треугольника. Составить уравнения медианы, высоты и биссектрисы угла А, найти их длины. Составить уравнения прямых, проходящих через вершины треугольника и параллельных его сторонам.

---

Смотрите также файлы

• Программа сезонной (летней) школы Центр весёлых ребят.docx

• Наименование норматива Условия выполнения норматива.docx

• Рубежный контроль 1 Форма рубежного контроля устный опрос.docx

• Здесь и ниже приведены рекомендации по заполнению шаблона Отчет о практике.doc

• Основы философии (часть 11) о22 Бондаренко.pdf