Файл: Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вопросы к экзамену
-
Строки. Префиксы, суффиксы, подстроки. Формальные языки.
Строка – это конечная последовательность символов а1, а2,…,аn, каж-й из кот-х принадлежит некоторому конечному алф-ту сигма Σ, при этом символы в строке могут повторяться.
Пустой строкой наз-т ε-строку ее длина-ноль, т.е. без единого символа. (не=пробелу). |x|=m-длина строки, т.е. строка содержит m символов.
Пусть Σ-некот-й алф-т, обозначим Σ* мн-во опред-х над этим алф-м строк. Для Σ={0,1}; Σ*= {ε,0,1,01,11,10,101,…} видно, что н-во Σ* - предс-т собой бесконечное счетное мн-во элем-в, ε-строка всегда  Σ*.
Σ*.
Пусть сущ-т строка х Σ* и |x|=m. Пусть сущ-т строка y
Σ* и |x|=m. Пусть сущ-т строка y Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.
Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.
Если х= а1, а2,…,аm; у= b1, b2,…,bn то |xy|= а1а2…аmb1b2...bn
Объединение – ассоциативная операция, но не коммуникативная.
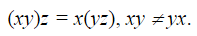
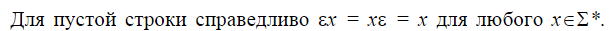
Если некоторая срока z м.б. представлена как объединение строк х и у: z=ху, то строку х наз-т префиксом строки z, а строку у-суффиксом. Если строка z т.ч. ее м/о представить как объединение 3х строк z=xwy, то строка w н-ся подстрокой строки z.
//z=аcab
префиксы: ε,a,ac,aca,acab
суффиксы: ε,b,ab,cab,acab
подстроки: ε,a,b,c,ac,ca,ab,aca,cab,acab
Разв-е теории и ср-в искус. интелекта позволяет надеяться на то, что взаимод-е чел-ка и ком-ра в недалеком будущем буд/т осуществляться на языке, близком к естественному. Но в наст. время, прог-ты в основном описывают задачи на формальных языках, на языках высокого уровня и иногда на ассемблере. Прог-мы, написанные на алгоритмических языках становятся доступными ком-ру, т/о после их трансляции, т.е. преобразования команд выс. ур/ня в машинные инструкции. Теория построения трансляторов базируется на теории формальных языков, особенно в части синтакс. и семантического разбора. (семантика – смысл, синтаксис – грамматика).
Формальным языком L над алф-ом Σ н-ся произвольное подмн-во мн-ва Σ*.
Если L1 и L2 это 2а формальных языка, то их объединение есть нов.форм.язык, т.ч.L= L1L2{xy| х L1,у
L1,у L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.
L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.
Для произвольного формального языка L справедливо 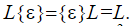
// L1={0,01} и L2={ε,0,10}значит L= L1L2={0,01,00,010,010,0110}
L0= ε, L1=L, L2=L*L -объединение форм. языка L с самим собой:

-
Дерево вывода. Синтаксическое и семантическое деревья. Примеры.
Правила, определяющие мн-ва текстов образ-т синтаксис языка, а описание мн-ва смыслов и соответствий м/у текстами и смыслами – семантику языка. Если в ест.языке допуск-ся некорректности в синтаксисе и м.б.понятен смысл предложения, то в формальных языках предложение в первую очередь должно быть правильным синтаксически.
Ф-ла Бэкуса-Наура(БНФ) исп-ся для описания синтаксиса языков прогр-ия, она использует след-щие 4 символа:
-
::= присвоить; 2) < - открыть; 3) > - закрыть; 4) | - или
//пр-р: The man drives a car.
<прост. предложение>::=<подфраза сущ.><глагол><подфр.сущ.>; <подфраза сущ-го>::=<артикль><имя сущ-ое>;
<имя сущ-ое>::= man,
<имя сущ-ое>::=car,
<артикль>::=the,
<артикль>::=a,
<глагол>::=drives
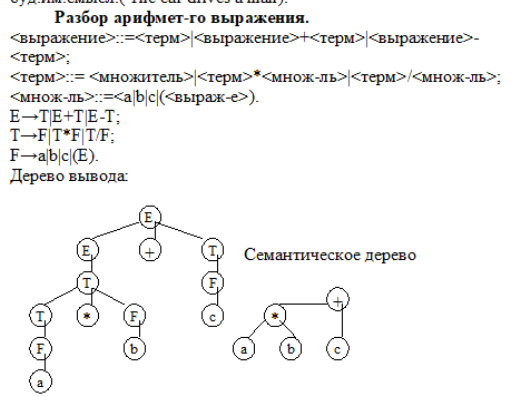
Связи, задаваемые ф-лой Б-Н м.б.представлены и графически в виде дерева-вывода:
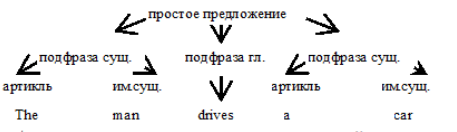
м/о построить мн-во простых предложений, удовлетворяющих дан.структуре и синтаксически правильных, но не все они буд.им.смысл.( The car drives a man).Таким образом, в зависимости от способа грамматического разбора изменяется смысл предложения. Этот пример показывает то важное для формальных языков обстоятельство, что грамматический разбор исходного текста программы, есть важнейший шаг на пути компиляции программы
. 
-
Контекстная грамматика. Контекстно-свободная грамматика.
Прописные буквы нетерминальные символы языка, строчные-терминальные, 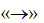 - определяется как.
- определяется как.
Всякое дерево вывода начинается с корня S в соответствии с правилами вывода происходит дв-е по ветвям строющегося дерева до тех пор, пока все нетерм-е символы не буд.раскрыты ч/з терм-е.
Контексная гр-ка(К/Г) – это совокуп-ть 4х объектов: G=(N,T,P,S), где
N-конеч.мн-во нетерм.симв-в,
T-кон.мн-во терм.симв,
P-кон.мн-во продук-й вида α→β, где a- строка в левой части продукции, такая что α (NUT)+-без пустой строки, β- строка в правой части, β
(NUT)+-без пустой строки, β- строка в правой части, β (NUT)*т.е. м/о получить и пуст.строку,
(NUT)*т.е. м/о получить и пуст.строку,
S-начальный символ.
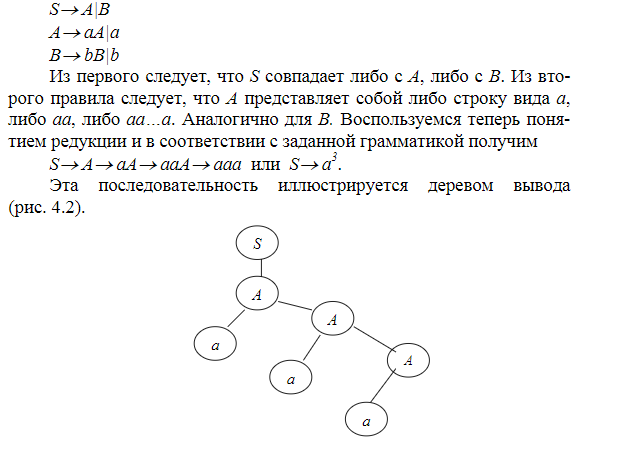
Если строка α  (NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S
(NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S  , то такую строку наз-т сентенциальной
, то такую строку наз-т сентенциальной
формой К/Г-ки G. (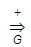 - обозначает транзитивное замыкание отношения
- обозначает транзитивное замыкание отношения 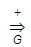 ,
, 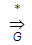 - рефлексивное замыкание отношения
- рефлексивное замыкание отношения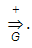 )Сентенцией гр-ки G наз-т произ-ю сентенциальную форму, составл-ю из симв-в мн-ва Т*, т.е.произ.строку терм.сим-в, кот-я м.б.получена из нач-го сим-ла S. Тогда мн-во всех сентенций гр-ки G наз-т языком, пораждаемым гр-кой G и обоз-т L(G). L(G)={x
)Сентенцией гр-ки G наз-т произ-ю сентенциальную форму, составл-ю из симв-в мн-ва Т*, т.е.произ.строку терм.сим-в, кот-я м.б.получена из нач-го сим-ла S. Тогда мн-во всех сентенций гр-ки G наз-т языком, пораждаемым гр-кой G и обоз-т L(G). L(G)={x Т* |
Т* |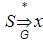 }.
}.
Если две грамматики порождают один и тот же язык, те 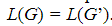 , то гр-ки G и G, эквивалентные. Язык грамматики- это все цепочки из терм-в, такое исп. Наз-ют выведением или порождением.
, то гр-ки G и G, эквивалентные. Язык грамматики- это все цепочки из терм-в, такое исп. Наз-ют выведением или порождением.
В форм. языках чаще всего в левой части продукции испол-ся 1н нетерм-й симв-л, кот-й явл-ся единс-м симв-м слева. К/Г-ка, удовл-щая этому требованию наз-ся КС/Г-ой. Строгое опред-е КС/Г-ки : гр-ка G=(N,T,P,S), в кот-й мн-во P содержит продук-ии вида α→β, где α N, β
N, β (NUT)*. Термин КС возник, т.к. люб. симв-л α
(NUT)*. Термин КС возник, т.к. люб. симв-л α N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.
N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.
КС/Г-ку м/о представить виде дерева вывода. Корнем кот-го явл-ся нач.символ S, строка терм-х симв-в, или сентенция – последов-ть висящих вершин, читаемых в порядке слева направа. Промеж-е узлы дерева– нетерм-е верш-ны. Если для люб. строки х L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α
L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α N, β
N, β (NUT)*. Значит корректна запись А→ε, где ε-терм. символ.
(NUT)*. Значит корректна запись А→ε, где ε-терм. символ.
Гр-ка не им-щая ε-прод-ции наз. ε-своб-й. Было бы идеально раб-ть т/о с ε-своб-ми гр-ми. Для преобр-ия гр-ки G в гр-ку G’, кот-я ε-своб-на н/о:
1. объединить все имеющиеся в Р ε-продукции в мн-во Р’.
2. все нетерм.сим-лы, т.ч. 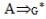 ε. Каж.прод-ции из Р’поставим в соотв-ие такую прод-цию, что в ее прав.части, посрав-ию с исход-й прод-ей Р опущены неск-ко нетермин-х сим-в.
ε. Каж.прод-ции из Р’поставим в соотв-ие такую прод-цию, что в ее прав.части, посрав-ию с исход-й прод-ей Р опущены неск-ко нетермин-х сим-в.
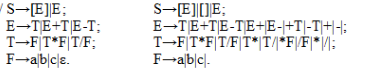
-
Регулярные грамматики и конечный автомат.

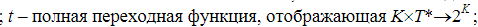

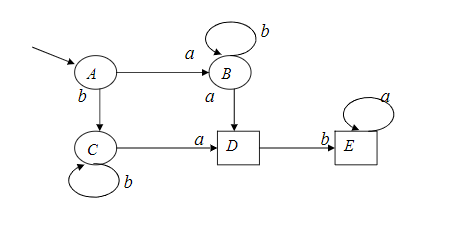
ДЕТЕРМИНИРОВАННЫЙ АВТОМАТ.
Для этого графа, функция t не полная, тк не определена на парах (D,a) и (E,b)
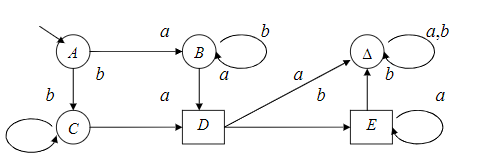
Если t неполная, можно добавить еще одно фиктивное состояние 

-
Эквивалентность автоматов.
Для каж-го конеч.ав-та сущ-т бескон-е кол-во др-х конеч-х ав-в, кот-е распоз-т те же цепочки. Но сущ-т единс-й кон.ав-т, кол-во состояний кот-го минимально. Два состояния наз.эквивалентными, если они одинаково реагируют на все продолжения входных цепочек. Состояние S конечного распознователя М экв-но сост-ю t кон-го распоз-ля N тогда и т/о тогда, когда авт-т М, начав работу в сост-ии S б/т допускать те же цепочки, что и ав-т N, начав работу в сост-ии t.
Из опред-ия эквив-х сост-й м/о дать опред-е экв-х авт-в: Авт-ты М и N экв-ны,тогда и т/о тогда, когда экв-ны их начальные состояния. Проверка экв-ти сост-й основывается на:
1.условие подобия, т.е.сост-я S и t должны  или к допуск-м, или к отвергающим.
или к допуск-м, или к отвергающим.
2.условие приемственности, т.е.для всех входных сим-в, сост-я S и t должны переходить в др-е эквивал-е сост-ия, т.е.их приемники д.б.эквив-ными.
(метод№1):метод таблиц экв-х сост-й.
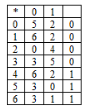
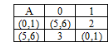
1.строется таблица эквив-сти сост-й(А), первыми запис-ся два начал-х сост-я, кот-е подверг-ся анализу.
2.выбирается строка в дан.таблице, ячейки кот-й еще не заполнены и проверяется подобны ли состояния, кот-ми она помечена. Если сост-я не подобны, то два исходных сост-я не эквив-ны и процесс завершен, если подобны, то вычисляется рез-т применения каж-го вход-го сим-ла к этой паре сост-й и записыв-сяполученные пары сост-й.
3. если пара разл-х сост-й(получ-х на 2 шаге) еще не использ-сь как метка, то она перепис-ся на новую строку.
4. если таблица завершена выписыв-ся все состояния, поражденные в ходе проверки,кот.б/т экв-ми сост-ми. В нашем пр-ре 0
1 и 5
6.
Сущ-т еще 1н метод №2:метод разбиения на непересекающиеся подмн-ва.
1.все мн-во сос-й разбив-ся на 2 блока, 1н блок содержит т/о отверг-е, др-й т/о доп-щие сост-ия. Ни одно сост-е 1-го блока не м.б.экв-но как.либо состоянию из 2-го блока. (см табл.*) Р1=({0,1,2,3},{4,5,6})
2.расс-м переходы в 1м блоке под возд-ем 0. из сост-й 0и1 переход в 5и6- доп-щие сост-ия, из 2и3 переход в 0и3-отверг-е сост-я, значит Р2=({0,1},{2,3},{4},{5,6}).
3.расс-е поведение блока {2,3} если на входе дей-т серия сим-в 0: они не экв-ны, Р3=({0,1},{2},{3},{4},{5,6}).
4.дальнейшие попытки разбить блок ={0,1}и {5,6}ничего не дают, значит 0
1 и 5
6.
Вопросы к экзамену
-
Строки. Префиксы, суффиксы, подстроки. Формальные языки.
Строка – это конечная последовательность символов а1, а2,…,аn, каж-й из кот-х принадлежит некоторому конечному алф-ту сигма Σ, при этом символы в строке могут повторяться.
Пустой строкой наз-т ε-строку ее длина-ноль, т.е. без единого символа. (не=пробелу). |x|=m-длина строки, т.е. строка содержит m символов.
Пусть Σ-некот-й алф-т, обозначим Σ* мн-во опред-х над этим алф-м строк. Для Σ={0,1}; Σ*= {ε,0,1,01,11,10,101,…} видно, что н-во Σ* - предс-т собой бесконечное счетное мн-во элем-в, ε-строка всегда  Σ*.
Σ*.
Пусть сущ-т строка х Σ* и |x|=m. Пусть сущ-т строка y
Σ* и |x|=m. Пусть сущ-т строка y Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.
Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.
Если х= а1, а2,…,аm; у= b1, b2,…,bn то |xy|= а1а2…аmb1b2...bn
Объединение – ассоциативная операция, но не коммуникативная.
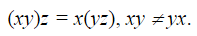
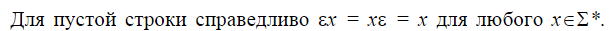
Если некоторая срока z м.б. представлена как объединение строк х и у: z=ху, то строку х наз-т префиксом строки z, а строку у-суффиксом. Если строка z т.ч. ее м/о представить как объединение 3х строк z=xwy, то строка w н-ся подстрокой строки z.
//z=аcab
префиксы: ε,a,ac,aca,acab
суффиксы: ε,b,ab,cab,acab
подстроки: ε,a,b,c,ac,ca,ab,aca,cab,acab
Разв-е теории и ср-в искус. интелекта позволяет надеяться на то, что взаимод-е чел-ка и ком-ра в недалеком будущем буд/т осуществляться на языке, близком к естественному. Но в наст. время, прог-ты в основном описывают задачи на формальных языках, на языках высокого уровня и иногда на ассемблере. Прог-мы, написанные на алгоритмических языках становятся доступными ком-ру, т/о после их трансляции, т.е. преобразования команд выс. ур/ня в машинные инструкции. Теория построения трансляторов базируется на теории формальных языков, особенно в части синтакс. и семантического разбора. (семантика – смысл, синтаксис – грамматика).
Формальным языком L над алф-ом Σ н-ся произвольное подмн-во мн-ва Σ*.
Если L1 и L2 это 2а формальных языка, то их объединение есть нов.форм.язык, т.ч.L= L1L2{xy| х L1,у
L1,у L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.
L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.
Для произвольного формального языка L справедливо 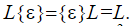
// L1={0,01} и L2={ε,0,10}значит L= L1L2={0,01,00,010,010,0110}
L0= ε, L1=L, L2=L*L -объединение форм. языка L с самим собой:

-
Дерево вывода. Синтаксическое и семантическое деревья. Примеры.
Правила, определяющие мн-ва текстов образ-т синтаксис языка, а описание мн-ва смыслов и соответствий м/у текстами и смыслами – семантику языка. Если в ест.языке допуск-ся некорректности в синтаксисе и м.б.понятен смысл предложения, то в формальных языках предложение в первую очередь должно быть правильным синтаксически.
Ф-ла Бэкуса-Наура(БНФ) исп-ся для описания синтаксиса языков прогр-ия, она использует след-щие 4 символа:
-
::= присвоить; 2) < - открыть; 3) > - закрыть; 4) | - или
//пр-р: The man drives a car.
<прост. предложение>::=<подфраза сущ.><глагол><подфр.сущ.>; <подфраза сущ-го>::=<артикль><имя сущ-ое>;
<имя сущ-ое>::= man,
<имя сущ-ое>::=car,
<артикль>::=the,
<артикль>::=a,
<глагол>::=drives
Связи, задаваемые ф-лой Б-Н м.б.представлены и графически в виде дерева-вывода:

м/о построить мн-во простых предложений, удовлетворяющих дан.структуре и синтаксически правильных, но не все они буд.им.смысл.( The car drives a man).Таким образом, в зависимости от способа грамматического разбора изменяется смысл предложения. Этот пример показывает то важное для формальных языков обстоятельство, что грамматический разбор исходного текста программы, есть важнейший шаг на пути компиляции программы
. 
-
Контекстная грамматика. Контекстно-свободная грамматика.
Прописные буквы нетерминальные символы языка, строчные-терминальные, 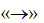 - определяется как.
- определяется как.

Всякое дерево вывода начинается с корня S в соответствии с правилами вывода происходит дв-е по ветвям строющегося дерева до тех пор, пока все нетерм-е символы не буд.раскрыты ч/з терм-е.
Контексная гр-ка(К/Г) – это совокуп-ть 4х объектов: G=(N,T,P,S), где
N-конеч.мн-во нетерм.симв-в,
T-кон.мн-во терм.симв,
P-кон.мн-во продук-й вида α→β, где a- строка в левой части продукции, такая что α (NUT)+-без пустой строки, β- строка в правой части, β
(NUT)+-без пустой строки, β- строка в правой части, β (NUT)*т.е. м/о получить и пуст.строку,
(NUT)*т.е. м/о получить и пуст.строку,
S-начальный символ.
Если строка α  (NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S
(NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S 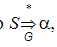 , то такую строку наз-т сентенциальной
, то такую строку наз-т сентенциальной
формой К/Г-ки G. (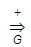 - обозначает транзитивное замыкание отношения
- обозначает транзитивное замыкание отношения 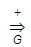 ,
, 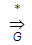 - рефлексивное замыкание отношения
- рефлексивное замыкание отношения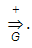 )Сентенцией гр-ки G наз-т произ-ю сентенциальную форму, составл-ю из симв-в мн-ва Т*, т.е.произ.строку терм.сим-в, кот-я м.б.получена из нач-го сим-ла S. Тогда мн-во всех сентенций гр-ки G наз-т языком, пораждаемым гр-кой G и обоз-т L(G). L(G)={x
)Сентенцией гр-ки G наз-т произ-ю сентенциальную форму, составл-ю из симв-в мн-ва Т*, т.е.произ.строку терм.сим-в, кот-я м.б.получена из нач-го сим-ла S. Тогда мн-во всех сентенций гр-ки G наз-т языком, пораждаемым гр-кой G и обоз-т L(G). L(G)={x Т* |
Т* |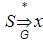 }.
}.
Если две грамматики порождают один и тот же язык, те 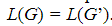 , то гр-ки G и G, эквивалентные. Язык грамматики- это все цепочки из терм-в, такое исп. Наз-ют выведением или порождением.
, то гр-ки G и G, эквивалентные. Язык грамматики- это все цепочки из терм-в, такое исп. Наз-ют выведением или порождением.
В форм. языках чаще всего в левой части продукции испол-ся 1н нетерм-й симв-л, кот-й явл-ся единс-м симв-м слева. К/Г-ка, удовл-щая этому требованию наз-ся КС/Г-ой. Строгое опред-е КС/Г-ки : гр-ка G=(N,T,P,S), в кот-й мн-во P содержит продук-ии вида α→β, где α N, β
N, β (NUT)*. Термин КС возник, т.к. люб. симв-л α
(NUT)*. Термин КС возник, т.к. люб. симв-л α N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.
N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.
КС/Г-ку м/о представить виде дерева вывода. Корнем кот-го явл-ся нач.символ S, строка терм-х симв-в, или сентенция – последов-ть висящих вершин, читаемых в порядке слева направа. Промеж-е узлы дерева– нетерм-е верш-ны. Если для люб. строки х L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α
L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α N, β
N, β (NUT)*. Значит корректна запись А→ε, где ε-терм. символ.
(NUT)*. Значит корректна запись А→ε, где ε-терм. символ.
Гр-ка не им-щая ε-прод-ции наз. ε-своб-й. Было бы идеально раб-ть т/о с ε-своб-ми гр-ми. Для преобр-ия гр-ки G в гр-ку G’, кот-я ε-своб-на н/о:
1. объединить все имеющиеся в Р ε-продукции в мн-во Р’.
2. все нетерм.сим-лы, т.ч. 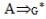 ε. Каж.прод-ции из Р’поставим в соотв-ие такую прод-цию, что в ее прав.части, посрав-ию с исход-й прод-ей Р опущены неск-ко нетермин-х сим-в.
ε. Каж.прод-ции из Р’поставим в соотв-ие такую прод-цию, что в ее прав.части, посрав-ию с исход-й прод-ей Р опущены неск-ко нетермин-х сим-в.
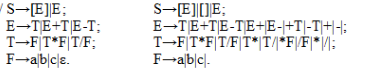
-
Регулярные грамматики и конечный автомат.

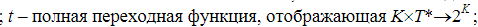


ДЕТЕРМИНИРОВАННЫЙ АВТОМАТ.
Для этого графа, функция t не полная, тк не определена на парах (D,a) и (E,b)

Если t неполная, можно добавить еще одно фиктивное состояние 

-
Эквивалентность автоматов.
Для каж-го конеч.ав-та сущ-т бескон-е кол-во др-х конеч-х ав-в, кот-е распоз-т те же цепочки. Но сущ-т единс-й кон.ав-т, кол-во состояний кот-го минимально. Два состояния наз.эквивалентными, если они одинаково реагируют на все продолжения входных цепочек. Состояние S конечного распознователя М экв-но сост-ю t кон-го распоз-ля N тогда и т/о тогда, когда авт-т М, начав работу в сост-ии S б/т допускать те же цепочки, что и ав-т N, начав работу в сост-ии t.
Из опред-ия эквив-х сост-й м/о дать опред-е экв-х авт-в: Авт-ты М и N экв-ны,тогда и т/о тогда, когда экв-ны их начальные состояния. Проверка экв-ти сост-й основывается на:
1.условие подобия, т.е.сост-я S и t должны  или к допуск-м, или к отвергающим.
или к допуск-м, или к отвергающим.
2.условие приемственности, т.е.для всех входных сим-в, сост-я S и t должны переходить в др-е эквивал-е сост-ия, т.е.их приемники д.б.эквив-ными.
(метод№1):метод таблиц экв-х сост-й.


1.строется таблица эквив-сти сост-й(А), первыми запис-ся два начал-х сост-я, кот-е подверг-ся анализу.
2.выбирается строка в дан.таблице, ячейки кот-й еще не заполнены и проверяется подобны ли состояния, кот-ми она помечена. Если сост-я не подобны, то два исходных сост-я не эквив-ны и процесс завершен, если подобны, то вычисляется рез-т применения каж-го вход-го сим-ла к этой паре сост-й и записыв-сяполученные пары сост-й.
3. если пара разл-х сост-й(получ-х на 2 шаге) еще не использ-сь как метка, то она перепис-ся на новую строку.
4. если таблица завершена выписыв-ся все состояния, поражденные в ходе проверки,кот.б/т экв-ми сост-ми. В нашем пр-ре 0
1 и 5
6.Вопросы к экзамену
-
Строки. Префиксы, суффиксы, подстроки. Формальные языки.
Строка – это конечная последовательность символов а1, а2,…,аn, каж-й из кот-х принадлежит некоторому конечному алф-ту сигма Σ, при этом символы в строке могут повторяться.
Пустой строкой наз-т ε-строку ее длина-ноль, т.е. без единого символа. (не=пробелу). |x|=m-длина строки, т.е. строка содержит m символов.
Пусть Σ-некот-й алф-т, обозначим Σ* мн-во опред-х над этим алф-м строк. Для Σ={0,1}; Σ*= {ε,0,1,01,11,10,101,…} видно, что н-во Σ* - предс-т собой бесконечное счетное мн-во элем-в, ε-строка всегда
 Σ*.
Σ*.Пусть сущ-т строка х
 Σ* и |x|=m. Пусть сущ-т строка y
Σ* и |x|=m. Пусть сущ-т строка y Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.
Σ* и |y|=n, тогда объединение строк ху им. длину |xy|=m+n – конкатенация.Если х= а1, а2,…,аm; у= b1, b2,…,bn то |xy|= а1а2…аmb1b2...bn
Объединение – ассоциативная операция, но не коммуникативная.
Если некоторая срока z м.б. представлена как объединение строк х и у: z=ху, то строку х наз-т префиксом строки z, а строку у-суффиксом. Если строка z т.ч. ее м/о представить как объединение 3х строк z=xwy, то строка w н-ся подстрокой строки z.
//z=аcab
префиксы: ε,a,ac,aca,acab
суффиксы: ε,b,ab,cab,acab
подстроки: ε,a,b,c,ac,ca,ab,aca,cab,acab
Разв-е теории и ср-в искус. интелекта позволяет надеяться на то, что взаимод-е чел-ка и ком-ра в недалеком будущем буд/т осуществляться на языке, близком к естественному. Но в наст. время, прог-ты в основном описывают задачи на формальных языках, на языках высокого уровня и иногда на ассемблере. Прог-мы, написанные на алгоритмических языках становятся доступными ком-ру, т/о после их трансляции, т.е. преобразования команд выс. ур/ня в машинные инструкции. Теория построения трансляторов базируется на теории формальных языков, особенно в части синтакс. и семантического разбора. (семантика – смысл, синтаксис – грамматика).
Формальным языком L над алф-ом Σ н-ся произвольное подмн-во мн-ва Σ*.
Если L1 и L2 это 2а формальных языка, то их объединение есть нов.форм.язык, т.ч.L= L1L2{xy| х
 L1,у
L1,у L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.
L2 } операция объединения формальных строк – ассоциативная операция, но не коммуникативная.Для произвольного формального языка L справедливо
// L1={0,01} и L2={ε,0,10}значит L= L1L2={0,01,00,010,010,0110}
L0= ε, L1=L, L2=L*L -объединение форм. языка L с самим собой:

-
Дерево вывода. Синтаксическое и семантическое деревья. Примеры.
Правила, определяющие мн-ва текстов образ-т синтаксис языка, а описание мн-ва смыслов и соответствий м/у текстами и смыслами – семантику языка. Если в ест.языке допуск-ся некорректности в синтаксисе и м.б.понятен смысл предложения, то в формальных языках предложение в первую очередь должно быть правильным синтаксически.
Ф-ла Бэкуса-Наура(БНФ) исп-ся для описания синтаксиса языков прогр-ия, она использует след-щие 4 символа:
-
::= присвоить; 2) < - открыть; 3) > - закрыть; 4) | - или
//пр-р: The man drives a car.
<прост. предложение>::=<подфраза сущ.><глагол><подфр.сущ.>; <подфраза сущ-го>::=<артикль><имя сущ-ое>;
<имя сущ-ое>::= man,
<имя сущ-ое>::=car,
<артикль>::=the,
<артикль>::=a,
<глагол>::=drives
Связи, задаваемые ф-лой Б-Н м.б.представлены и графически в виде дерева-вывода:

м/о построить мн-во простых предложений, удовлетворяющих дан.структуре и синтаксически правильных, но не все они буд.им.смысл.( The car drives a man).Таким образом, в зависимости от способа грамматического разбора изменяется смысл предложения. Этот пример показывает то важное для формальных языков обстоятельство, что грамматический разбор исходного текста программы, есть важнейший шаг на пути компиляции программы
.

-
Контекстная грамматика. Контекстно-свободная грамматика.
Прописные буквы нетерминальные символы языка, строчные-терминальные,

Всякое дерево вывода начинается с корня S в соответствии с правилами вывода происходит дв-е по ветвям строющегося дерева до тех пор, пока все нетерм-е символы не буд.раскрыты ч/з терм-е.
Контексная гр-ка(К/Г) – это совокуп-ть 4х объектов: G=(N,T,P,S), где
N-конеч.мн-во нетерм.симв-в,
T-кон.мн-во терм.симв,
P-кон.мн-во продук-й вида α→β, где a- строка в левой части продукции, такая что α
 (NUT)+-без пустой строки, β- строка в правой части, β
(NUT)+-без пустой строки, β- строка в правой части, β (NUT)*т.е. м/о получить и пуст.строку,
(NUT)*т.е. м/о получить и пуст.строку,S-начальный символ.
Если строка α
 (NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S
(NUT)* за 1н или неск-ко шагов выводится из начального сим-ла S формой К/Г-ки G. (
 Т* |
Т* |Если две грамматики порождают один и тот же язык, те
В форм. языках чаще всего в левой части продукции испол-ся 1н нетерм-й симв-л, кот-й явл-ся единс-м симв-м слева. К/Г-ка, удовл-щая этому требованию наз-ся КС/Г-ой. Строгое опред-е КС/Г-ки : гр-ка G=(N,T,P,S), в кот-й мн-во P содержит продук-ии вида α→β, где α
 N, β
N, β (NUT)*. Термин КС возник, т.к. люб. симв-л α
(NUT)*. Термин КС возник, т.к. люб. симв-л α N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.
N в сентанц. форме гр-ки G м.б.раскрыт согласно продукции из α→β,независимо от того, какими строками он окружен внутри самой сент. формы.КС/Г-ку м/о представить виде дерева вывода. Корнем кот-го явл-ся нач.символ S, строка терм-х симв-в, или сентенция – последов-ть висящих вершин, читаемых в порядке слева направа. Промеж-е узлы дерева– нетерм-е верш-ны. Если для люб. строки х
 L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α
L(G) все возможные схемы вывода имеют одно и тоже дерево вывода, то гр-ка наз. однозначная КС/Г-кой. (S→AB; A→aA|a; B→bB|b –строка а3b2). Если одной и той же строке соотв-т разл. деревья, то гр-ка наз. неоднозна-й (S→SbS|ScS|a-строка abaca). В дан.опред-ии КС/Г-ки ее продукции им.вид: α→β, где α N, β
N, β (NUT)*. Значит корректна запись А→ε, где ε-терм. символ.
(NUT)*. Значит корректна запись А→ε, где ε-терм. символ.Гр-ка не им-щая ε-прод-ции наз. ε-своб-й. Было бы идеально раб-ть т/о с ε-своб-ми гр-ми. Для преобр-ия гр-ки G в гр-ку G’, кот-я ε-своб-на н/о:
1. объединить все имеющиеся в Р ε-продукции в мн-во Р’.
2. все нетерм.сим-лы, т.ч.
-
Регулярные грамматики и конечный автомат.



ДЕТЕРМИНИРОВАННЫЙ АВТОМАТ.
Для этого графа, функция t не полная, тк не определена на парах (D,a) и (E,b)

Если t неполная, можно добавить еще одно фиктивное состояние

-
Эквивалентность автоматов.
Для каж-го конеч.ав-та сущ-т бескон-е кол-во др-х конеч-х ав-в, кот-е распоз-т те же цепочки. Но сущ-т единс-й кон.ав-т, кол-во состояний кот-го минимально. Два состояния наз.эквивалентными, если они одинаково реагируют на все продолжения входных цепочек. Состояние S конечного распознователя М экв-но сост-ю t кон-го распоз-ля N тогда и т/о тогда, когда авт-т М, начав работу в сост-ии S б/т допускать те же цепочки, что и ав-т N, начав работу в сост-ии t.
Из опред-ия эквив-х сост-й м/о дать опред-е экв-х авт-в: Авт-ты М и N экв-ны,тогда и т/о тогда, когда экв-ны их начальные состояния. Проверка экв-ти сост-й основывается на:
1.условие подобия, т.е.сост-я S и t должны
 или к допуск-м, или к отвергающим.
или к допуск-м, или к отвергающим.2.условие приемственности, т.е.для всех входных сим-в, сост-я S и t должны переходить в др-е эквивал-е сост-ия, т.е.их приемники д.б.эквив-ными.
(метод№1):метод таблиц экв-х сост-й.


1.строется таблица эквив-сти сост-й(А), первыми запис-ся два начал-х сост-я, кот-е подверг-ся анализу.
2.выбирается строка в дан.таблице, ячейки кот-й еще не заполнены и проверяется подобны ли состояния, кот-ми она помечена. Если сост-я не подобны, то два исходных сост-я не эквив-ны и процесс завершен, если подобны, то вычисляется рез-т применения каж-го вход-го сим-ла к этой паре сост-й и записыв-сяполученные пары сост-й.
3. если пара разл-х сост-й(получ-х на 2 шаге) еще не использ-сь как метка, то она перепис-ся на новую строку.
4. если таблица завершена выписыв-ся все состояния, поражденные в ходе проверки,кот.б/т экв-ми сост-ми. В нашем пр-ре 0
Сущ-т еще 1н метод №2:метод разбиения на непересекающиеся подмн-ва.
1.все мн-во сос-й разбив-ся на 2 блока, 1н блок содержит т/о отверг-е, др-й т/о доп-щие сост-ия. Ни одно сост-е 1-го блока не м.б.экв-но как.либо состоянию из 2-го блока. (см табл.*) Р1=({0,1,2,3},{4,5,6})
2.расс-м переходы в 1м блоке под возд-ем 0. из сост-й 0и1 переход в 5и6- доп-щие сост-ия, из 2и3 переход в 0и3-отверг-е сост-я, значит Р2=({0,1},{2,3},{4},{5,6}).
3.расс-е поведение блока {2,3} если на входе дей-т серия сим-в 0: они не экв-ны, Р3=({0,1},{2},{3},{4},{5,6}).
4.дальнейшие попытки разбить блок ={0,1}и {5,6}ничего не дают, значит 0
-
Аксиомы и основные теоремы булевой алгебры
Аксиомы:
1. Аксиомы конъюнкции 0·* 0 = 0 ; 1·* 1 = 1 ; 0·* 1 = 1·* 0 = 0 ;
2. Аксиомы дизъюнкции 0 v 0 = 0 ; 1 v 1 = 1 ; 0 v 1 = 1 v 0 = 1 ;
3. Аксиомы отрицания Если x = 0 , то ˆх = 1 ;
Если x = 1 , то ˆх = 0 ;
Теоремы:
4. Операции с константами:
5. Идемпотентность (тавтология, повторение):
Для n переменных:
6. Противоречие :
7. Правило "исключенного третьего":
8. Двойное отрицание (инволюция):
Законы (тождества):
9. Ассоциативность (ассоциативный закон) :
10. Коммутативность (коммутативный закон) :
11. Дистрибутивность (дистрибутивный закон) :
конъюнкции относительно дизъюнкции:
дизъюнкции относительно конъюнкции:
12. Законы де Моргана (законы инверсии или отрицания) :
13. Поглощение :
14. Закон Блейка-Порецкого :
15. Склеивание (объединение) :
- 1 2 3 4
Теорема о структурной полноте В.М.Глушкова.
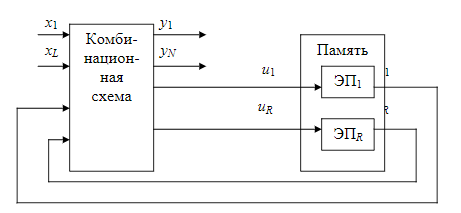
Автомат представляется как совокупность 2 частей- памяти и комбинационной схемы. ЭП-iый элемент памяти, x- входные каналы автомата, y- выходные каналы автомата, u – ф-я возбуждения памяти автомата, v- обратной связи автомата.
Теорема о структурной полноте Глушкова: для того, чтобы система элементарных автоматов была структурно полной необходимо и достаточно, чтобы она содержала хотя бы один автомат мура с полной системой переходов и полной системой выходов, а также функционально полную систему логических элементов
Автомат мура обладает полной системой переходов, если для любой пары состояний (ai,aj) найдётся входной сигнал, переводящий один элемент пары в другой, включая случай, когда i=j.
Автомат мура обладает полной системой выходов, если каждое состояние автомата отмечено выходным сигналом, отличным от сигналов, отмечающих остальные состояния. Элементарным автоматом называется автомат с двумя состояниями. Логический элемент - интегральная схема реализующая булеву функцию.
.
-
Канонический метод структурного синтеза автоматов (Модель дискретного преобразователя В.М.Глушкова)
Комбинационная схема (КС) может иметь несколько выходов. При каноническом методе предполагается, что каждая выходная функция реализуется своей схемой, совокупность которых и даёт требуемую КС. Поэтому синтез сложной КС с n выходами заменяется синтезом n схем с одним выходом. Согласно каноническому методу синтез КС включает в себя ряд этапов.
1. Подлежащая реализации булева функция (или её отрицание) представляется в виде СДНФ.
2. С использованием методов минимизации определяется минимальная ДНФ (МДНФ) или минимальная КНФ (МКНФ). Из полученных двух минимальных форм выбирается более простая.
3. Булеву функцию в минимальной форме согласно п.2 представляют в заданном (или выбранном разработчиком) базисе .
4. По представлению функции в заданном базисе строят комбинационную схему.
Необходимо отметить, что подлежащая реализации булева функция F(X1,X2,...,Xm) может быть задана не на всех возможных наборах аргументов X1, X2, ..., Xm. На тех наборах, где функция неопределенна, её доопределяют так, чтобы в результате минимизации получить более простую МДНФ или МКНФ. При этом упростится и сама КС. Кроме того, довольно часто с целью получения ещё более простого представления функции МДНФ, полученная в п.2, представляется в так называемой скобочной форме, т.е. выносятся за скобки общие части импликант МДНФ.
Авт-т любой сложности представл в виде структуры,сост из 2-х частей:

В схеме след обозначения: X1-XL – множ-во входных сигналов структурного авт-та Y1-YN – множ-во выходных сигналов U1-UR – множ-во сигналов возбуждения ЭП V1-VR – множ-во сигналов обратной связи
Теорема Глушкова (Система элементарных автоматов явл структурно полной тогда и только тогда,когда содержит:
1)авт-ты Мура,облад полнотой переходов и выходов.
2).комбинацион схему,постороенную на функционал полной системе логических элементов. В этом случае задача структурного синтеза произвольных автоматов сводится к задаче структурного синтеза комбинационных схем).
В соответ-ии с теоремой Глушкова задача синтеза структ авт-та сост в построении комбинац части.Математически это записыв-ся так: y1=y1(x1,x2,…,xL,V1,V2,…,VR)…
yN=yN(x1,x2,…,xL,V1,V2,…VR)
U1=U1(x1,x2,…,xL,V1,V2,…VR)…
UR=UR(x1,x2,…,xL,V1,V2,…VR).
Т.о.,задача синтеза структурного авт-та сводится к составлению и решению этой сист логических уравнений.
-
СДНФ( по 1) и СКНФ( по 0)

Минтермы- произведение
Макстермы- сумма


-
Синтез автомата на D- и RS-триггерах.

-
СНФ в базисе «Стрелка Пирса» и «Штрих Шеффера»


отрицаем, где 0

Для обозначения логических принципиальных схемах используют спец изображения

-
Графический метод структурного синтеза автоматов.

