Аппаратные противогоночные средства: импульсная синхронизация, двойная память, апериодические схемы.

Для искл-я опасных состяназний исп. спец. противогоночное кодирование либо аппаратные средства.К ним относят:1)выравнивание задержек по различным цепям распространения сигналов;2)импульсную синхронизацию; 3)двухступенчатую (двойную) память;4)апериодические схемы.

1)Метод выравнивания задержек состоит в том, что в более быстрые цепи включаются дополнительные логические элементы, не изменяющие логику работы цепи, но увеличивающие время прохождения сигнала по ней.2)В методе импульсной синхронизации в качестве ЭП используются синхронные элементарные автоматы. В них имеется вход синхронизации, и как бы ни менялись управляющие входы триггера, при наличии запрета на этом входе состояние триггера не изменится.  3)В автомате с 2ой памятью гонки устраняются путем разделения во времени процесса выработки сигналов возбуждения и процесса переключения состояний.В качестве элементов памяти исп. MS-триггеры. 4) При использовании апериодической схемотехники проблема гонок решается полностью. Внешняя синхронизация отсутствует, поэтому такие схемы иногда называют самосинхронизирующимися. Идея самосинхронизации состоит в том, что в схеме определяются точки, в которых сходятся сигналы, получившие разные задержки в процессе их формирования, и в этих точках устанавливаются так называемые семафоры. Семафоры запрещают встречу всех сигналов до тех пор, пока не придет самый задержанный из них. Таким образом, распространение сигналов по цепям схемы, в том числе и ко входам элементов памяти, происходит по специальным разрешающим сигналам, формируемым самой схемой по фактическому времени задержек. Естественно, что в этом случае, кроме полного исключения эффекта гонок, достигается максимально возможное для данной схемы быстродействие.

21. 
    Связь между моделями Мура и Мили.
    

Между автоматами Мура и Мили существует однозначная связь - каждому автомату Мура можно поставить в соответствие эквивалентный автомат Мили и наоборот(эквивалентность автоматов - одинаковость реакций автоматов на все возможные цепочки входных символов).

---

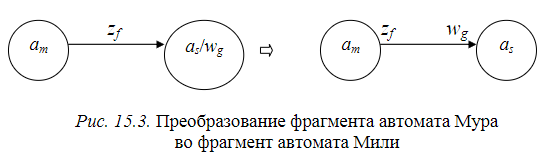
Выходной сигнал w_g, записанный в вершине a_s, переносится на все дуги, входящие в эту вершину. При табличном способе задания автомата Мура таблица переходов автомата Мили совпадает с таблицей переходов автомата Мура, а таблица выходов автомата Мили получается из таблицы переходов заменой символа a_s, стоящего на пересечении строки z_f и столбца a_m, символом выходного сигнала w_g, отмечающего столбец a_s в отмеченной таблице переходов автомата Мура.
Функцию выходов λ_s и переходов δ_s определим так. Каждому состоянию автомата Мура, представляющему собой пару вида (a_s, w_g), поставим в соответствие выходной сигнал w_g. Если в автомате Мили был переход δ_R(a_m,z_f) = a_s и при этом выдавался выходной сигнал λ_R(a_m, z_f) = w_k, то в автомате Мура будет переход из множества состояний A_m, порождаемых a_m, в состояние (a_s,w_k) под действием того же входного сигнала z_f :

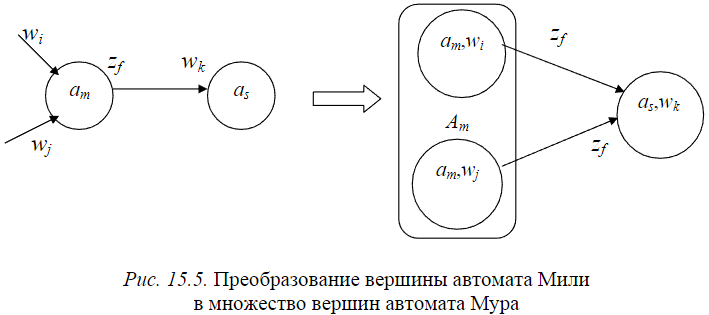
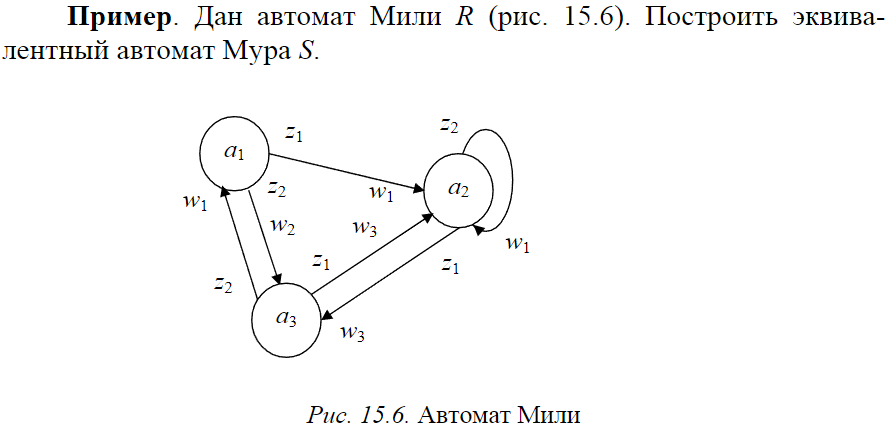
Пример. Дан автомат Мили R(рис. 15.6). построить эквивалентный автомат Мура S.

22. 
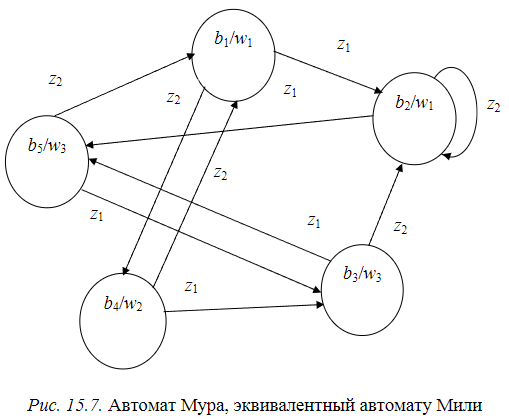
    Базисы логических функций.
    

Базис (функционально полный набор) ­­– это множество логических функций, суперпозицией которых можно представить любую логическую формулу, т. е. полная система логических функций.
Базисы могут быть избыточными и минимальными. Например, система функций И, Или, НЕ (булев базис, базис Буля) – избыточный базис, так как при удалении из него некоторых функций (функции ИЛИ или функции И) система остаётся полной.
Минимальными базисами являются системы: 1) И, НЕ; 2) ИЛИ, НЕ; 3) И-НЕ (базис Шеффера); 4) ИЛИ-НЕ (базис Пирса). При удалении из таких базисов любой операции они перестают быть полными системами функций.
Одни и те же преобразования логических переменных можно задать в раз­личных формах (базисах). Выбор базиса зависит от простоты реализации той или иной функции с помощью логических операций данной системы функций. Чаще всего используются базисы Шеффера и Пирса, т. к. они содержат только одну операцию, и для реализации сложной схемы нужен только один тип ЛЭ. В развитых сери­ях стандартных интегральных схем (ИС) наряду с базовыми ЛЭ обычно имеется и ряд других, выполняющих другие логические операции.

---

23. 
    Абсолютно минимальные формы представления ФАЛ.
    

Методы минимизации,как метод карт Карно или Квайна-Мак-Класски дают ответ в классе нормальных форм.Но если отказаться от представления ф-ии в виде нормальной формы,то можно получить ещё более простую запись и более простую реализацию логических ф-ий.

Существует оптимальный алгоритм представления ф-ий в скобочной форме,он разработан только для булева базиса и наз факторным алгоритмом.\

1).дана ф-ия,представленная в виде ДНФ.В этой ф-ии каждый из термов обозначается одной буквой.

2).вычисляются все попарные пересечения (∩) этих термов(напр-р,x₁ вошёл и в первый и во второй терм).

3).из полученных пересечений выбираются пересечения максимального ранга(max кол-во переменных в терме).Если таковых несколько,то выбор безразличен.

4).полученные термы обозначаются заново

5).вновь вычисляются все попарные пересечения и выбирается терм max ранга.

6).новый вид ф-ии называется абсолютно минимальной формой.

Например,f(x1,x2,x3,x4) = x1x2 Vx1x3x4  можно представить в виде f(x1,x2.x3.x4) = x1(x2 V X3x4). Второе представление содержит две

коньюнкции и одну дизъюнкцию, а первое - три коньюнкции и одну дизъюнкцию, т.е. второе представление более экономично.

Дано

1)Обозначаем конъюнктивные термы как abcd

2)Найдем пересечения термов  и выбираем max ранг((a,d)(a,c)(c,d)), возьмем (C ,D)

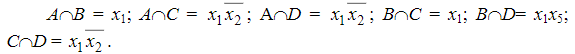
3) Запишем функцию f, вынося общий элемент x1*не(x2) за скобки в C+D



4) вводим новые обозначения и повторяем шаги, пока окончательно не получим

Данная форма имеет 6 конъюнкций и 3 дизъюнкции, а исходная 11 кон. и 3 диз..

24. 
    Построение комбинационной схемы автомата. Ограничения по базису, по количеству входов и выходов.
    

Задача синтеза: по заданному множ-ву входных переменных и по заданному множ-ву логических ф-ий построить цифровую схему,реализующую эту функцию. При этом необходимо учесть ограничения:синтезировать в заданном базисе,учесть ограничения по числу входов и выходов логических элементов,учесть ограничения на время и.т.д. При решении задач синтеза схем используют простейшую их классификацию:

---

1).схемы с несколькими входами и одним выходом. Задача сост в том,что логическую ф-ию нескольких переменных представляют в заданном базисе(штрих Шеффера или стрелка Пирса) с минимальной сложностью и с учётом ограничений на число входов и выходов.Задачу минимизации можно решить двумя способами:1.ф-ия минимизируется в булевом базисе,а рез-т преобразуется в требуемый базис.2.ф-ия сразу записывается в требуемый базис и минимизируется в нём.Т.к. для булова базиса наиболее широко разработаны методы преобразования и минимизации,а также исходные ф-ии чаще всего заданы именно в нём,то 1-ый способ используется чаще.

2).схемы с несколькими входами и несколькими выходами. Задача построения таких схем возникает в том случае,если требуется реализовать систему логических уравнений,причём кол-во выходов в схеме равно числу уравнений в системе,а кол-во входов определяется числом переменных,на которых построена данная система.Эту задачу можно решить двумя способами:

а).рассмотреть каждую ф-ию системы в отдельности и разработать схему,состоящую из k-отдельных схем,каждая из которых представляет собой схему с несколькими входами и одним выходом.k-число ф-ий в системе.Недостатком этого способа является то,что результируемая схема будет иметь большую избыточность,т.к. некоторые фрагменты отдельных схем могут повторяться.Достоинством метода является простота.

б).всю схему,реализующую систему логических выражений,можно представить в виде (n,k)-полюсника,где n-число входов, k-число выходов.При этом подходе учитываются внутренние взаимосвязи между ф-ями.В рез-те схемы получаются проще,но процедура синтеза сложнее.

25. 
    Полнота переходов и полнота выходов автомата Мура.
    

26. 
    Синтез комбинационных (n,k)-полюсников
    

n-кол-во переменных, k-кол-во выходов схем.

2 способа решений:

1. 
   решается отдельно k задач без исп-я связей м/у уравнениями.
   
2. 
   решение сист. урав. с целью поиска повторяющихся аргументов. Решение сложное, но получается более простой ответ.
   

---

Пр-р

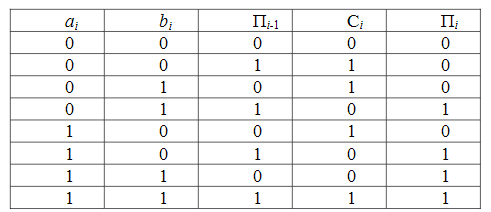
1 метод:



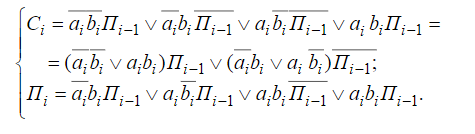
Минимизируем( Пi- картами карно)



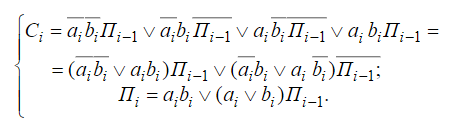
ci - 6К и 3Д

Пi -  2К и 2Д

схема



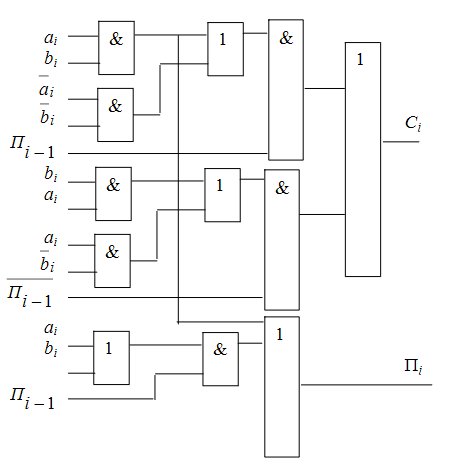
2 метод:

Если предположить что Пi уже сформирован можно переписать в виде



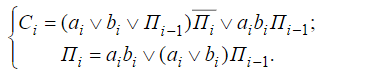
ci - 3К и 3Д

Пi -  2К и 2Д Более простое решение

схема



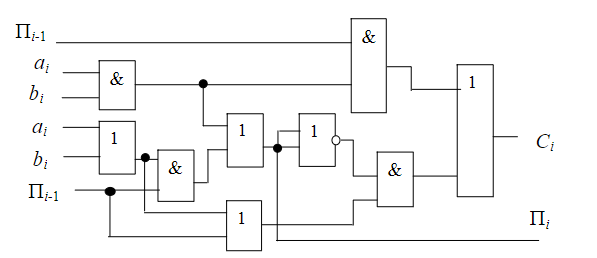
Наиболее удобным для синтеза многовыходных схем яв-ся метод с применением карт Карно. Строится k карт Карно, во всех картах ищется одинаково помеченные клетки(ядро).

27. 
    Элементарные автоматы.
    

В качестве ЭП используют элементарные авт-ты Мура,отвечающие условиям теоремы Глушкова (Система элементарных автоматов явл структурно полной тогда и только тогда,когда содержит:1)авт-ты Мура,облад полнотой переходов и выходов. 2).комбинацион схему,постороенную на функционал полной системе логических элементов. В этом случае задача структурного синтеза произвольных автоматов сводится к задаче структурного синтеза комбинационных схем).

В настоящее время-это триггеры. Триггер – это устройство, имеющее два устойчивых состояния(0,1), в которые он переходит под действием определённых входных сигналов.Обычно в триггерах выделяют два вида входных сигналов (и соответственно входов): информационные и синхросигналы.Информационные сигналы определяют новое состояние триггера и присутствуют в любых триггерах. Синхросигнал не является обязательным и вводится в триггерах с целью фиксации момента перехода триггера в новое состояние, задаваемое информационными входами. Обычно, при синтезе ЦА используются триггеры с синхровходом. На синхровход триггера поступают тактирующие импульсы задающего генератора, синхронизирующего работу ЦА. Период следования импульсов соответствует одному такту автоматного времени ЦА. Триггер имеет два выхода прямой и инверсный.

---

Смотрите также файлы

• Федеральное государственное бюджетное образовательное учреждениевысшего образования.docx

• Теория денег на современном этапе.docx

• Нефтяная промышленность.pptx

• Права в арабском востоке современность.docx

• Категории сотрудников Сокращенное время.docx