Файл: Вопросы к экзамену Строки. Префиксы, суффиксы, подстроки. Формальные языки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Состояние триггера определяется по прямому выходу.
RS-триггер.Вход S (set) называется входом установки в единицу, вход R (reset) – входом установки в нуль.
Таблица функций выходов и условное обозначение:
На основании таблицы можно получить функцию возбуждения памяти автомата при синтезе на базе RS-триггеров. Например, если автомат переходит из состояния ai= 010 в состояние aj=110, то для обеспечения такого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 R1 =0, S1 = 1;
для второго триггера при переходе из 1 в 1 R2 =0, S2 = X;
для третьего триггера при переходе из 0 в 0 R3 =X, S3= 0.
Т-триггер.(триггер со счётным входом). Имеет один информационный вход Т и два выхода прямой и инверсный. Осуществляет суммирование по модулю два значений сигнала T и состояний Q и Qинверсноев заданный момент времени.
Таблица функций выходов и условное обозначение:
На основании этой таблицы можно получать функцию возбуждения элементов памяти при синтезе автомата на базе T-триггера. Например, если автомат перешел из состояния ai = 010 в состояние aj = 110, то для обеспечения этого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 T1
= 1,
для второго триггера при переходе из 1 в 1 T2 = 0,
для третьего триггера при переходе из 0 в 0 T3 =0 .
D-триггер.(элемент задержки).Имеет один информационный вход D и два выхода прямой и инверсный, и осуществляет задержку поступившего на его вход сигнала на один такт.
Таблица функций выходов и условное обозначение:
На основании этой таблицы можно получать функцию возбуждения элементов памяти при синтезе автомата на базе D-триггера. Например, если автомат перешел из состояния ai = 010 в состояние aj = 110, то для обеспечения этого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 D1 = 1,
для второго триггера при переходе из 1 в 1 D2 = 1,
для третьего триггера при переходе из 0 в 0 D3 =0 .
Минимизация сложности комбинационных схем: аналитический метод, метод Карт Карно (3,4,5 переменных).
Критерием сложности к реализации является колич-во переменных и знаков логических д-ий в представляемой ф-ии.
Основная идея минимизации сост в выполнении операции склеивания,в рез-те которой уменьшается кол-во термов и ранг полученных термов меньше ранга исходных.Термы,отлич-ся значением одной переменной,наз соседними.
Суть аналитического метода сост в том,что к исходной записи ф-ии непосредственно примен-ся аксиомы и теоремы алгебры логики.
F(x,y,z)=xyz + xy + z = xy(z+1)+z = xy + z.
Метод Карт Карно:
1).исходная ф-ия представл в виде СДНФ
2) Минтермы, образующие СДНФ, заносятся в карту Карно в соответствующие клетки в виде “1”. Пустые “0”.
3).выделение групп.Каждая группа-это множ-во соседних клеток,заполненных единицами,причём колич-во клеток в группе м.б.=2,4,8…2k. Нужно стремится к тому чтобы групп было как можно меньше, но сами они были как можно больше.
4).анализ групп и склеивание.Если группа содержит две соседних клетки,то в рез-те склеивания получается терм,имеющий ранг на единицу меньший,чем исходный терм.Если группа сод-т четыре соседних клетки,то ранг рез-та уменьшен на два.Если в группе k-соседей,то ранг рез-та уменьшен на k.
5) полученные после склеивания термы объединяются знаком дизъюнкции.
Карты Карно 5-ти переменных им особенности:
1.группы д.б. симметричны относительно разделяющей линии.2.м.б. группы,имеющие аналитическое,но не геометрическое соседство.Такие группы следует искать в симметричных относительно разделительной линии столбцах.
Примеры базисов.
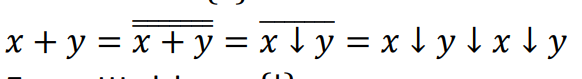
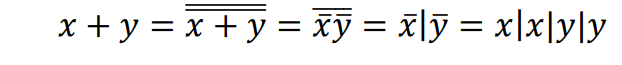
7Сокращенный базис Буля (ИЛИ-НЕ)
8Универсальный базис Буля (И-НЕ)
Логические ф-ии м.б. представлены различным количеством переменных и знаком логических д-ий.Основная идея минимизации сост в выполнении операции склеивания,в рез-те которой уменьшается кол-во термов и ранг полученных термов меньше ранга исходных.Термы,отлич-ся значением одной переменной,наз соседними.
Сначала метод был предложен Квайном,суть кот сост в том,что составлялась таблица,где в столбцах и строках перебирались все термы,входящие в минимизируемую функцию,представленную в виде СДНФ.Если некоторая пара склеивалась,то в соответствующую клетку таблицы вписывался рез-т склеивания.Результаты склеивания формировали вторую таблицу и т.д.Недостаток сост в том,что обработка происходила в символьных изображениях и была трудоёмка при большом колич-ве переменных.Мак-Класски ввёл двоичное представление термов, вместо символьного,что позволило резко снизить кол-во перебираемых пар.
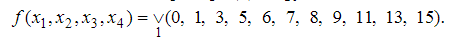
1)Выписываются 0-кубы. 0000, 0001, 0011,0101,0110,0111,1000, 1001,1101,1111
2)0-ые кубы группируются по кол-ву 1 в них.
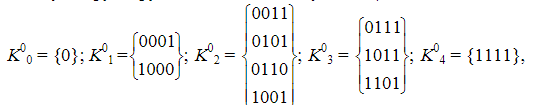
3) Склеивание 0-ых кубов в 1-ые кубы, только м/у соседними кубами, особое внимание на термы, которые не участвовали в склеивании- претенденты на ответ. В данном примере таких нет.
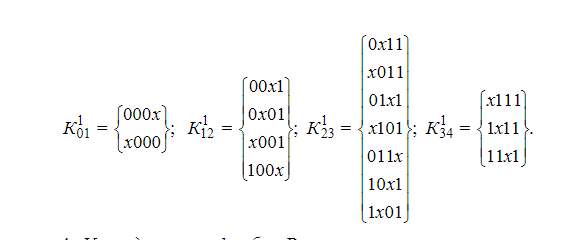
4).упорядочивание одномерных кубов по месту расположения x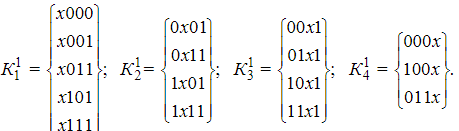
5)Склеивание внутри 1-кубов. 011x не участвовал в склеивании
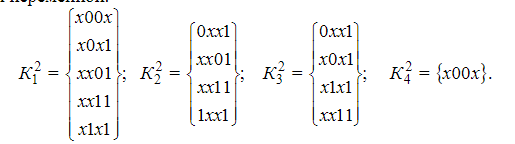
6).вычёркивание одной из двух одинаковых импликант
7).построение и заполнение таблицы для поиска минимального покрытия.По горизонтали выписываются все исходные нульмерные кубы в двоичной форме,а по вертикали-оставшиеся простейшие импликантыи и те импликанты,которые ни разу не участвовали в склеивании.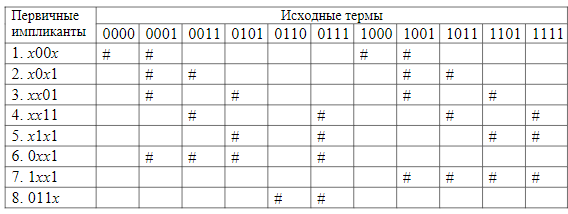
Проверка:-не д.б. столбцов,не имеющих хотя однц метку; -каждая строка должна содерж точно 2k-клеток,гдк k-колич-во крестов в вертикальном первом столбце таблицы.8) вычеркивание столбцов, помеченных существенными импликантами.
8).поиск минимального покрытия начинается с поиска существенных импликант.Импликанта-терм,входящий в состав термов,образующих ф-ию.Существенная импликанта порождает единственную метку в столбце.Такая импликанта обязательно входит в окончательный ответ.Если присутсствуют несущественные импликанты(имеющие несколько меток в соответ столбцах),то в ответ войдут некоторые из них.Сама процедура выбора одной из нескольких несуществующих импликант наз поиском минимального покрытия,состоящая в вычёркивании столбцов,порождающие существенные импликанты. Выписываем ответ 011x +x00x+0xx1+1xx1
___________________Вопрос 33____________________
Синтез комбинационных схем по не полностью определенным ФАЛ
Если значения ф-и на нек-х наборах не заданы, то она называется не полностью определенной.
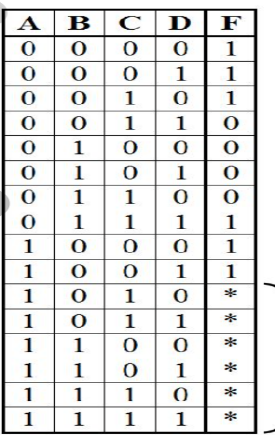
Пусть дана ф-ия от n-переменных:f(x1,x2,…,xn). Если функция нк определена на n наборах, то ее можно доопределить 2^n наборов способами, доведя до определенной ф-й таких, что они будут совпадать с ф-ией f на всех определённых наборах Т.к. можно построить 2p различных эквивалентных ф-ий, то возникает задача, какую конкретно из них выбрать, чтобы её сложность была минимальной. Чаще всего такие задачи решаются с пом карт Карно.
___________________Вопрос 35____________________
Синтез комбинационных схем на дешифраторах и мультиплексорах
Дешифратор - схема реализующая все конституенты единицы.ДШ имеет n входов и 2^n выходов. Синтез ДШ сводится к дизъюнктивному объединению необходимых выходов ДШ. Объединение дешифратора с помощью мультиплексора.
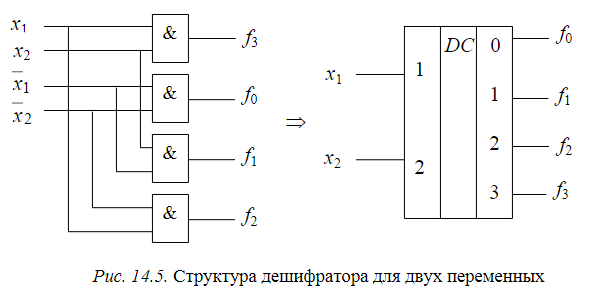
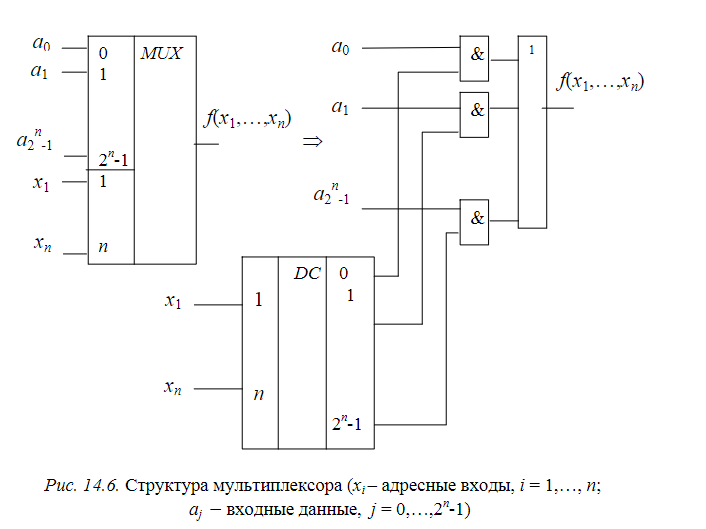
Мультиплексор- схема с 1 выходом и 2мя группами входов: данных и адресными
RS-триггер.Вход S (set) называется входом установки в единицу, вход R (reset) – входом установки в нуль.
| Qt | Qt+1 | R | S |
| 0 | 0 | X | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | X |
На основании таблицы можно получить функцию возбуждения памяти автомата при синтезе на базе RS-триггеров. Например, если автомат переходит из состояния ai= 010 в состояние aj=110, то для обеспечения такого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 R1 =0, S1 = 1;
для второго триггера при переходе из 1 в 1 R2 =0, S2 = X;
для третьего триггера при переходе из 0 в 0 R3 =X, S3= 0.
Т-триггер.(триггер со счётным входом). Имеет один информационный вход Т и два выхода прямой и инверсный. Осуществляет суммирование по модулю два значений сигнала T и состояний Q и Qинверсноев заданный момент времени.
Таблица функций выходов и условное обозначение:
| Qt | Qt+1 | Tt |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
На основании этой таблицы можно получать функцию возбуждения элементов памяти при синтезе автомата на базе T-триггера. Например, если автомат перешел из состояния ai = 010 в состояние aj = 110, то для обеспечения этого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 T1
= 1,
для второго триггера при переходе из 1 в 1 T2 = 0,
для третьего триггера при переходе из 0 в 0 T3 =0 .
D-триггер.(элемент задержки).Имеет один информационный вход D и два выхода прямой и инверсный, и осуществляет задержку поступившего на его вход сигнала на один такт.
Таблица функций выходов и условное обозначение:
| Qt | Qt+1 | Dt |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
На основании этой таблицы можно получать функцию возбуждения элементов памяти при синтезе автомата на базе D-триггера. Например, если автомат перешел из состояния ai = 010 в состояние aj = 110, то для обеспечения этого перехода функции возбуждения должны быть:
для первого триггера при переходе из 0 в 1 D1 = 1,
для второго триггера при переходе из 1 в 1 D2 = 1,
для третьего триггера при переходе из 0 в 0 D3 =0 .
- 1 2 3 4
Минимизация сложности комбинационных схем: аналитический метод, метод Карт Карно (3,4,5 переменных).
Критерием сложности к реализации является колич-во переменных и знаков логических д-ий в представляемой ф-ии.
Основная идея минимизации сост в выполнении операции склеивания,в рез-те которой уменьшается кол-во термов и ранг полученных термов меньше ранга исходных.Термы,отлич-ся значением одной переменной,наз соседними.
Суть аналитического метода сост в том,что к исходной записи ф-ии непосредственно примен-ся аксиомы и теоремы алгебры логики.
F(x,y,z)=xyz + xy + z = xy(z+1)+z = xy + z.
Метод Карт Карно:
1).исходная ф-ия представл в виде СДНФ
2) Минтермы, образующие СДНФ, заносятся в карту Карно в соответствующие клетки в виде “1”. Пустые “0”.
3).выделение групп.Каждая группа-это множ-во соседних клеток,заполненных единицами,причём колич-во клеток в группе м.б.=2,4,8…2k. Нужно стремится к тому чтобы групп было как можно меньше, но сами они были как можно больше.
4).анализ групп и склеивание.Если группа содержит две соседних клетки,то в рез-те склеивания получается терм,имеющий ранг на единицу меньший,чем исходный терм.Если группа сод-т четыре соседних клетки,то ранг рез-та уменьшен на два.Если в группе k-соседей,то ранг рез-та уменьшен на k.
5) полученные после склеивания термы объединяются знаком дизъюнкции.
Карты Карно 5-ти переменных им особенности:
1.группы д.б. симметричны относительно разделяющей линии.2.м.б. группы,имеющие аналитическое,но не геометрическое соседство.Такие группы следует искать в симметричных относительно разделительной линии столбцах.
-
Понятие базиса логических функций. Примеры
Примеры базисов.
-
Базис Буля: {∧, v, ¬} -
Базис Жегалкина: {1,⊕,&} -
Конъюктивный базис: {&; −} -
Дизъюктивный базис: {+; −} -
Базис Вебба: {↓}
-
Базис Шеффера: {|}
7Сокращенный базис Буля (ИЛИ-НЕ)
8Универсальный базис Буля (И-НЕ)
-
Минимизация сложности комбинационных схем: метод Квайна-Мак-Класски
Логические ф-ии м.б. представлены различным количеством переменных и знаком логических д-ий.Основная идея минимизации сост в выполнении операции склеивания,в рез-те которой уменьшается кол-во термов и ранг полученных термов меньше ранга исходных.Термы,отлич-ся значением одной переменной,наз соседними.
Сначала метод был предложен Квайном,суть кот сост в том,что составлялась таблица,где в столбцах и строках перебирались все термы,входящие в минимизируемую функцию,представленную в виде СДНФ.Если некоторая пара склеивалась,то в соответствующую клетку таблицы вписывался рез-т склеивания.Результаты склеивания формировали вторую таблицу и т.д.Недостаток сост в том,что обработка происходила в символьных изображениях и была трудоёмка при большом колич-ве переменных.Мак-Класски ввёл двоичное представление термов, вместо символьного,что позволило резко снизить кол-во перебираемых пар.
1)Выписываются 0-кубы. 0000, 0001, 0011,0101,0110,0111,1000, 1001,1101,1111
2)0-ые кубы группируются по кол-ву 1 в них.
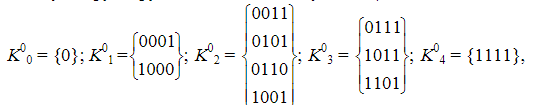
3) Склеивание 0-ых кубов в 1-ые кубы, только м/у соседними кубами, особое внимание на термы, которые не участвовали в склеивании- претенденты на ответ. В данном примере таких нет.
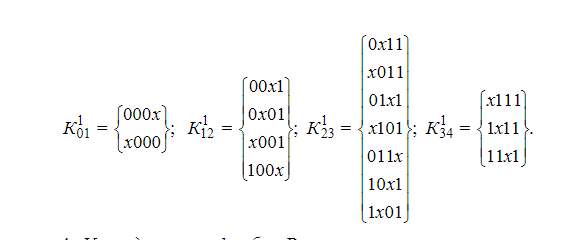
4).упорядочивание одномерных кубов по месту расположения x
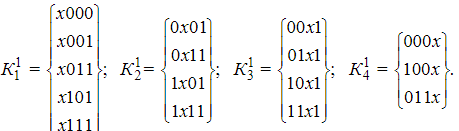
5)Склеивание внутри 1-кубов. 011x не участвовал в склеивании
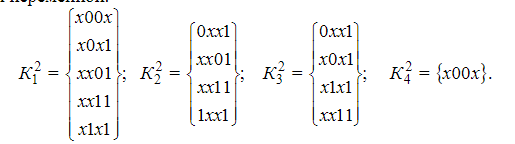
6).вычёркивание одной из двух одинаковых импликант
7).построение и заполнение таблицы для поиска минимального покрытия.По горизонтали выписываются все исходные нульмерные кубы в двоичной форме,а по вертикали-оставшиеся простейшие импликантыи и те импликанты,которые ни разу не участвовали в склеивании.

Проверка:-не д.б. столбцов,не имеющих хотя однц метку; -каждая строка должна содерж точно 2k-клеток,гдк k-колич-во крестов в вертикальном первом столбце таблицы.8) вычеркивание столбцов, помеченных существенными импликантами.
8).поиск минимального покрытия начинается с поиска существенных импликант.Импликанта-терм,входящий в состав термов,образующих ф-ию.Существенная импликанта порождает единственную метку в столбце.Такая импликанта обязательно входит в окончательный ответ.Если присутсствуют несущественные импликанты(имеющие несколько меток в соответ столбцах),то в ответ войдут некоторые из них.Сама процедура выбора одной из нескольких несуществующих импликант наз поиском минимального покрытия,состоящая в вычёркивании столбцов,порождающие существенные импликанты. Выписываем ответ 011x +x00x+0xx1+1xx1
___________________Вопрос 33____________________
Синтез комбинационных схем по не полностью определенным ФАЛ
Если значения ф-и на нек-х наборах не заданы, то она называется не полностью определенной.

Пусть дана ф-ия от n-переменных:f(x1,x2,…,xn). Если функция нк определена на n наборах, то ее можно доопределить 2^n наборов способами, доведя до определенной ф-й таких, что они будут совпадать с ф-ией f на всех определённых наборах Т.к. можно построить 2p различных эквивалентных ф-ий, то возникает задача, какую конкретно из них выбрать, чтобы её сложность была минимальной. Чаще всего такие задачи решаются с пом карт Карно.
___________________Вопрос 35____________________
Синтез комбинационных схем на дешифраторах и мультиплексорах
Дешифратор - схема реализующая все конституенты единицы.ДШ имеет n входов и 2^n выходов. Синтез ДШ сводится к дизъюнктивному объединению необходимых выходов ДШ. Объединение дешифратора с помощью мультиплексора.

Мультиплексор- схема с 1 выходом и 2мя группами входов: данных и адресными


