1. 
   Вычислим регулярную составляющую (тренд):
   

а) Рассчитаем среднее значение для каждого года (столбца). Результаты внесем в таблицу 3.2.


б) Построим график изменения средних значений объемов продаж, перебирая типы уравнений регрессии. Наиболее точно описывающее точки из таблицы является линейная регрессия вида: y = 1,3904x + 200,03. Коэффициенты уравнения записываем рядом с графиком.


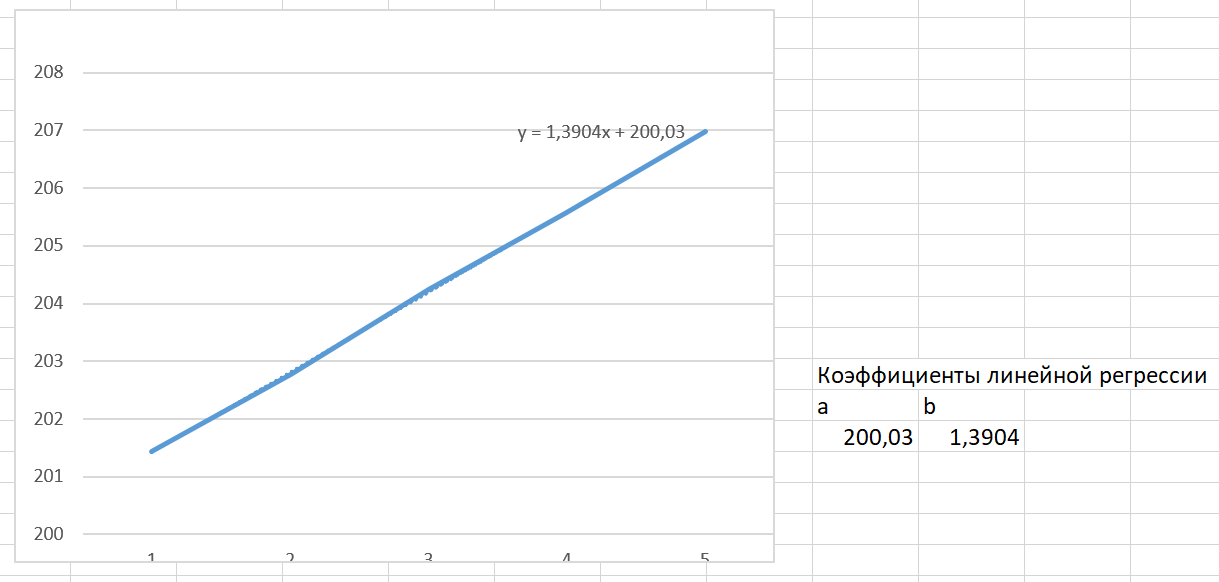
2. Вычислим сезонную компоненту (волну):

а) Сформируем таблицу 3.3 вычитанием из таблицы 3.1 соответствующих среднегодовых значений таблицы 3.2. Усредним значения по каждому месяцу и запишем в таблицу 3.3 в соответствии с месяцем в столбец «Средние».

б) С помощью «Мастера Диаграмм» построим график изменения средних значений по месяцам. Вставим линию тренда и подберем тип регрессии. Наилучшим образом описывающая точки графика является полиноминальная регрессия вида: y = 0,7101x² - 9,2146x + 21,432. Коэффициенты уравнения запишем рядом с диаграммой.

3. 
   Вычислим случайную составляющую.
   

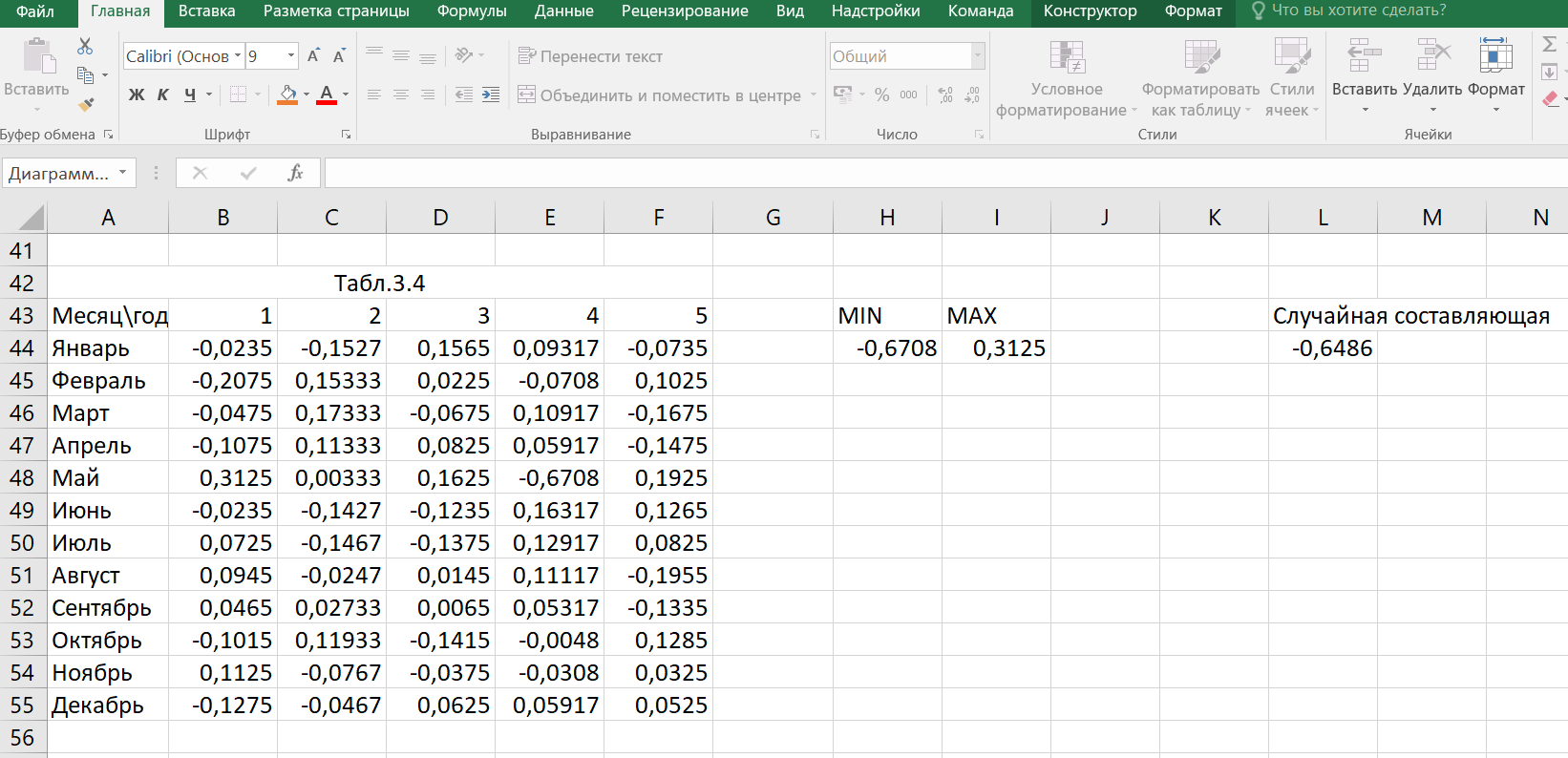
а) сформируем таблицу 3.4 вычитанием из среднемесячного значения (столбец «средние») всех значений таблицы 3.3 соответствующего месяца. Найдем минимальное (MIN) и максимальное (MAX) значение в таблице 3.4.

4. 
   Используя полученную модель, сделаем прогноз на февраль будущего года.
   

Значение тренда равно 208,372. Значение волны равно 31,6072. После суммирования значений тренда, волны и случайной составляющей получаем прогноз цены на февраль следующего года равный 239,331. Полученная модель с учетом случайной составляющей, сезонной составляющей(волны) и основного направления(тренда) движения цены позволяет Сделать прогноз, что в феврале следующего года цена на акции составит 239,4228. Согласно прогнозу, цена на акции будет расти. Цена на акции в феврале будет иметь максимальное значение за последние 5 лет, согласно прогнозу.

---

Вопросы для проверки:

1. 
   Объясните, в чем суть прогнозирования экономических процессов на основе метода динамических рядов?
   

Суть прогнозирования экономических процессов на основе метода динамических рядов заключается в анализе и статистическом описании динамики какого-либо существенного колеблющегося показателя. Прогнозирование экономических процессов на основе метода динамических рядов начинается с выявления формы его тренда. После этого приступают к статистической оценке параметров тренда. В соответствии с определением тренда, форма его объективна и отражает закономерности развития изучаемого процесса. Задача исследователя заключается в выявлении реально существующей формы тренда, а затем уже в выборе того уравнения (типа линии), которое наилучшим образом аппроксимирует объективный тренд. С позиций признания объективного характера формы тренда исходный пункт исследования самого процесса развития заключается в выявлении его материальной природы, внутренних причин развития и его внешних условий. Такое исследование может установить ожидаемую форму тренда. Теоретический анализ тренда дополняется исследованием его формы по фактическому динамическому ряду, что позволяет выявить тип тренда и измерить его конкретные параметры.

2. 
   Какие компоненты входят в состав динамического ряда?
   

При анализе динамических рядов используется также понятие сезонности (цикличности), характеризующее какие-либо периодические колебания данного ряда, и понятие случайного отклонения под воздействием каких-либо случайных факторов. В общем случае каждый член динамического ряда { Y_t }, где t существует в интервале от 1 до T, может быть представлен в аддитивной форме, содержащей несколько составляющих:

Y_t U_t V_t  E_t  Z_t  n_t,

где U_t - тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию;

V_t - сезонная компонента или внутригодичные колебания, а в общем случае – циклическая составляющая;

E_t - случайная компонента, образующаяся под влиянием различных неизвестных причин

---

;

Z_t - компонента, обеспечивающая сопоставимость элементов динамического ряда;

n_t - управляющая компонента, с помощью которой воздействуют на члены динамического ряда с целью формирования в будущем его желаемой траектории (управляемый прогноз).

3. 
   Каким образом происходит расчет каждой из составляющих ряда?
   

Вычисление регулярной компоненты Ut (тренда).

Известны несколько методов вычисления регулярной компоненты. К ним относятся: механические способы сглаживания, аналитические методы с применением определенных математических функций и, наконец, комбинированный способ.
Расчет компоненты Z_t

Имеется временной ряд данных по месяцам за несколько лет. Примем, что в каждом месяце 25 рабочих дней. Введем следующие обозначения:

r_t - фактическое число рабочих дней в определенном месяце;

T - принятое количество рабочих дней в каждом месяце ( T = 25);

Y_t - значение ряда в месяце t;

Y_t¹- значение ряда, соответствующее 25 рабочим дням в месяце.

Компонента Z_t может быть вычислена как:


Вычисление сезонной V_t и случайной E_t компонент.

Для определения сезонной и случайной компонент вычисляется динамический ряд:

V_t  E_t  Y_t  (U_t  Z_t), при n_t =0.

Сезонная и случайная компоненты представляют собой составляющие временного ряда, которые остаются после выделения из него тренда и выравнивающей компоненты, при условии, что управляющая компонента равна нулю. При разделении сезонной и случайной компонент обычно первой вычленяют сезонную компоненту, а оставшуюся часть временного ряда относят к случайной составляющей.

Среднесезонное значение может быть найдено как


Для нахождения случайной составляющей E_t временной ряд следует привести к сопоставимому виду, сезонную компоненту и тренд необходимо отфильтровать и вычесть из значений Y_t, управление n_t должно отсутствовать.

---

4. 
   Как оценить адекватность трендовой модели?
   

Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по уравнению тренда) уровни ряда достаточно близко подходят к фактическим их значениям, т.е.  и  мало отличаются друг от друга. Для оценки адекватности модели проводится анализ остатков .

Модели тенденции также можно сравнивать по величине остаточной суммы квадратов:  . Чем меньше эта величина, тем в большей степени уравнение тренда подходит для описания тенденции временного ряда.

Другим показателем при выборе функции тренда является коэффициент детерминации R². Чем выше R², тем выше вероятность того, что данная модель тенденции описывает исходные данные. Величина 1- R² отражает влияние случайной составляющей, т.е. показывает, какая доля вариации уровней динамического ряда не связана с тенденцией.

Однако рассмотренные критерии адекватности модели тенденции (S и R²) могут привести к неправильным выводам, если не учитывать статистическую значимость параметров уравнения тренда.

Уравнение тренда хорошо описывает тенденцию, если отсутствует автокорреляция в остатках, т.е. остатки текущего периода не коррелируют с остатками предыдущего периода. Измерить автокорреляцию в остатках можно с помощью коэффициента автокорреляции остатков:

.

Чем ближе коэффициент автокорреляции остатков  к нулю, тем больше оснований говорить об отсутствии связи между соседними величинами остатков.

5. 
   Почему рекомендуют автоматизировать работы по прогнозированию при разработке управленческих решений?
   

---

Работы по прогнозированию при разработке управленческих решений рекомендуется автоматизировать, так как обычно прогнозирование опирается на рутинные расчеты, выполнение которых вручную требует значительных затрат времени и которые приводят к различным просчетам и ошибкам. Во время ручной работы не остается достаточного времени для поиска оптимальных вариантов, поэтому планирование ограничивается первым непротиворечивым планом. С помощью автоматизации сокращается время поиска варианта, а также реализуется возможность проведения их сравнительного анализа.

Практическая работа № 5
Имитационное моделирование. Планирование компьютерного эксперимента

Вариант 4

При планировании двухфакторного эксперимента были вычислены параметры линейной модели, линейной модели со смешанными оценками и нелинейной модели, построены графики функций. Согласно графикам функций адекватными моделями являются линейная модель и модель со смешанными оценками. При оценке адекватности моделей по значениям сумм квадратов отклонений также можно сделать вывод, что линейная модель(сумма квадратов отклонений равна 0,84) и модель со смешанными оценками(сумма квадратов отклонений равна 0,78) являются адекватными и наиболее точно описывают экспериментальную функцию.
Вопросы для проверки:

1. 
   Как рассчитать число серий эксперимента N?
   

Для полного факторного эксперимента, в котором реализуются все возможные сочетания уровней факторов, число опытов определяется по следующей формуле:

N = A^k , где N - число опытов; k - число факторов, A-число уровней

Для двухуровневого эскперимента формула имеет вид:

N = 2^k

2. 
   Чем отличается линейная модель, нелинейная модель и линейная модель со смешанными оценками?
   

При планировании эксперимента следует начинать с линейной модели

---

Смотрите также файлы

• Основы безопасности жизнедеятельности. Учение о безопасности. Предмет и.docx

• Выполнение практических заданий по дисциплине принятие и исполнение государственных решений.docx

• 1. Гражданин ограничен в дееспособности .pdf

• Самостоятельная работа по теме 4 Задание Заполните таблицу Факторы формирования личности человека.docx

• Саба азаты лтты ойындарына баулу. Мектеп.docx