(Y_лин = A₀ +A₁*X₁+A₂*X₂). Если результаты не будут удовлетворять поставленным требованиям, то необходимо перейти к рассмотрению более сложных моделей. Линейная и линейная модель со смешанными(Y _лс = A₀ +A₁*X₁+A₂*X₂ +A₁₂*X₁*X₂) оценками требуют изменения факторов на двух уровнях. Линейная модель со мешанными оценками отличается от линейной модели наличием дополнительного слагаемого A₁₂*X₁*X₂, отражающего взаимодействие двух факторов. Такие эффекты взаимодействия, хотя и малы по сравнению с линейными, но все же не равны нулю. Нелинейная модель

(Y _н = A₀ +A₁*X₁+A₂*X₂ +A₁₂*X₁*X₂ + +A₁₁*X₁^2 + A₂₂*X₂^2) – описывается тремя уровнями изменения факторов и учитывает взаимодействие факторов, находящихся на разных уровнях.

3. 1   2   3   4

---

Как оценить адекватность моделей?


Числом степеней свободы в статистике называется разность между числом опытов и числом коэффициентов (констант), которые уже вычислены по результатам этих опытов независимо друг от друга. Остаточная сумма квадратов, деленная на число сте­пеней свободы, называется остаточной диспер­сией, или дисперсией адекватности 

.

В статистике разработан критерий, который очень удобен для проверки гипотезы об адекватности модели. Он называется F-критерием Фишера и определяется сле­дующей формулой:

.

 – это дисперсия воспроизводимости со своим числом степеней свободы.

Удобство использования критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с табличным значением.

Если рассчитанное значение F-критерия не превы­шает табличного, то, с соответствующей доверительной вероятностью, модель можно считать адекватной. При превышении табличного значения эту гипотезу приходится отвергать.

Этот способ расчета дисперсии адекватности, подходит, если опыты в матрице планирования не дублируются, а информация о дисперсии воспроизводимости извлекается из параллельных опытов в нулевой точке или из предварительных экспериментов. Важны два случая: 1) опыты во всех точках плана дублируются одинаковое число раз (равномерное дублирование), 2) число параллельных опытов не одинаково (неравномерное дублирование).

В первом случае дисперсию адекватности нужно умножать на n, где n – число повторных опытов

  .

Такое видоизменение формулы вполне естественно. Чем больше число параллельных опытов, тем с большей достоверностью оцени­ваются средние значения. Поэтому требования к различиям между экспериментальными и расчетными значениями становятся более жесткими, что отражается в увеличении 

---

F-критерия.

Во втором случае, когда приходится иметь дело с неравномер­ным дублированием, положение усложняется. Даже когда экспе­риментатор задумал провести равное число параллельных опытов, часто не удается по тем или иным причинам все их реализовать. Кроме того, иногда приходится отбрасывать отдельные опыты как выпадающие наблюдения.

При неравномерном дублировании нарушается ортогональность матрицы планирования и, как следствие, изменяются расчетные фор­мулы для коэффициентов регрессии и их ошибок, а также для дис­персии адекватности.

Для дисперсии адекватности можно записать общую формулу

,

где N – число различных опытов (число строк матрицы);

n_i – число параллельных опытов в i-й строке матрицы;

 – среднее арифметическое из n_i параллельных опытов;

 – предсказанное по уравнению значение в этом опыте.

Смысл этой формулы очень прост: различию между эксперимен­тальным и расчетным значением придается тем больший вес, чем больше число повторных опытов.

Для b-коэффициентов нельзя записать универсальную рас­четную формулу. Все зависит от того, какой был план и как дубли­ровались опыты. Всякий раз приходится делать специальные рас­четы, пользуясь методом наименьших квадратов.

Практическая работа № 6

Системы массового обслуживания

Вариант 4

Задание

Одноканальная система массового обслуживания с отказами представляет собой одну телефонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов λ=0,7 (вызовов в минуту). Средняя продолжительность разговора мин. Все потоки событий – простейшие. Определить предельные (при ) значения:

1. 
   Относительной пропускной способности q;
   
2. 
   Абсолютной пропускной способности A;
   
3. 
   Вероятности отказа P_отк
   

---

Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый разговор длился в точности 1,8 мин, и разговоры следовали бы один за другим без перерыва.

Решение:

Определяем параметр µ потока обслуживаний:

.

Вычислим относительную пропускную способность q:

.

Таким образом, в установившемся режиме система будет обслуживать около 44% поступающих вызовов.

Находим абсолютную пропускную способность:

,

Т.е. линия способна осуществить в среднем 0,309 разговоров в минуту.

Вероятность отказа:

,

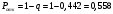Значит, около 56% поступивших вызовов будет получать отказ

Номинальная пропускная способность канала:

(разговора в минуту),

Что почти вдвое больше(в 1,8 раз), чем фактическая пропускная способность, полученная с учетом случайного характера потока заявок и случайности времени обслуживания.

Вопросы для проверки:

1. 
   Охарактеризуйте системы массового обслуживания.
   

Системы массового обслуживания (СМО) – класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

Характерным для работы таких систем является случайное появление заявок на обслуживание и завершение обслуживания случайные моменты времени, то есть стохастический характер их функционирования.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и само обслуживание заявки. Основными элементами СМО являются входной поток заявок, входной поток обслуживаний, очереди заявок, ожидающих обслуживания, каналы обслуживания и выходной поток обслуженных заявок и заявок, которым по тем или иным причинам в обслуживании отказано.

---

СМО классифицируют по следующим признакам:

а) по количеству каналов обслуживания они делятся на одноканальные и многоканальные СМО;

б) по организации ожидания заявки – на системы с отказами и системы с ожиданием или с очередями (накопителями)

в) СМО с накопителями, в свою очередь, делятся на системы с приоритетами и без приоритетов;

г) по количеству фаз обслуживания – на однофазные и многофазные;

д) по взаимосвязи с потоками заявок – на разомкнутые и замкнутые.

Эффективность работы СМО характеризуется следующими основными показателями:

1. 
   абсолютная пропускная способность – среднее количество заявок, которое может обслужить система в единицу времени;
   
2. 
   относительная пропускная способность – отношение среднего числа заявок, обслуженных СМО в единицу времени, к среднему числу всех заявок, поступивших в СМО за это же время;
   
3. 
   коэффициент занятости – отношение среднего числа занятых каналов к общему числу каналов;
   
4. 
   коэффициент простоя – отношение среднего числа свободных каналов к общему числу каналов.
   

2. 
   Как рассчитать вероятность отказа?
   

Вероятность отказа СМО определяется по формуле:

, где q- это относительная пропускная способность.

3. 
   Как рассчитать пропускную способность системы?
   

Относительную пропускную способность q можно рассчитать по формуле , где λ - интенсивность потока заявок, – это среднее число заявок

Абсолютная пропускная способность рассчитывается по формуле:

, где λ - интенсивность потока заявок, q - относительная пропускная способность

---

Смотрите также файлы

• Основы безопасности жизнедеятельности. Учение о безопасности. Предмет и.docx

• Выполнение практических заданий по дисциплине принятие и исполнение государственных решений.docx

• 1. Гражданин ограничен в дееспособности .pdf

• Самостоятельная работа по теме 4 Задание Заполните таблицу Факторы формирования личности человека.docx

• Саба азаты лтты ойындарына баулу. Мектеп.docx