Файл: Для анализа зависимости цены автомобиля y от его возраста Х.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 18.10.2024

Просмотров: 9

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




Задача 1
В базе данных магазина, торгующего подержанными автомобилями, содержится информация об их потребительский свойствах и ценах.

Для анализа зависимости цены автомобиля Y от его возраста Х1 и мощности двигателя Х2 из базы данных выбраны сведения о 16 автомобилях. Эти сведения приведены в таблице1.


номер
цена
возраст
мощность

1
14,4
4
154

2
16,9
2
155

3
13
5
149

4
9,6
7
128

5
9,8
7
134

6
9,6
7
127

7
16,8
2
157

8
14,8
4
160

9
9,8
7
134

10
16,9
2
154

11
16
3
161

12
17,4
2
167

13
17,2
2
163

14
17,4
2
163

15
15,7
3
155

16
17,1
2
162




  1. Парные зависимости

    1. Построить поля рассеяния для цены Y и возраста автомобиля Х1, а также для цены Y и мощности двигателя Х2. На основе их визуального анализа выдвинуть гипотезы о виде статистической зависимости Y от Х1 и Y от Х2 и записать их математически.


Построим поля рассеяния:



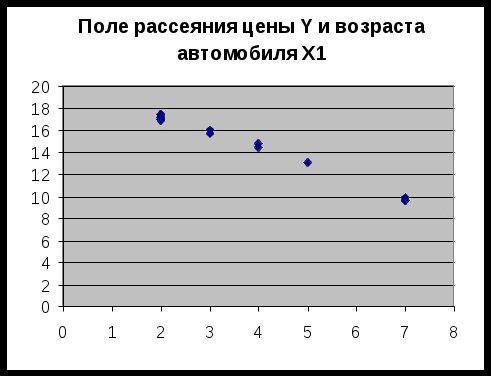
Рис. 1. Поле рассеяния для цены Y и возраста автомобиля Х1



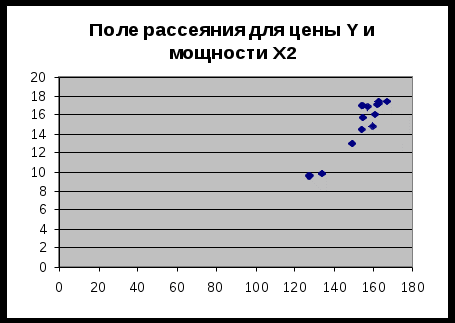
Рис. 2 Поле рассеяния для цены Y и мощности двигателя Х2
На основе визуального анализа построенных полей рассеяния можно выдвинуть гипотезу о линейной зависимости цены от возраста Х1 и мощности двигателя Х2.

Математически данные зависимости запишутся в виде:

y = α0+ α1x1 +

и y = β0+ β1x1 + , где и - случайные переменные.
1.2. Методом наименьших квадратов найти оценки линейных уравнений регрессии:

y = α0+ α1x1, y = β0+ β1x1.

Составим вспомогательную таблицу для = α0+ α1x1: (таблица 2)

i
yi

xi1

xi12
yi xi1
yi2

1
14,4
4
16
57,6
207,36

2
16,9
2
4
33,8
285,61

3
13
5
25
65
169

4
9,6
7
49
67,2
92,16

5
9,8
7
49
68,6
96,04

6
9,6
7
49
67,2
92,16

7
16,8
2
4
33,6
282,24

8
14,8
4
16
59,2
219,04

9
9,8
7
49
68,6
96,04

10
16,9
2
4
33,8
285,61

11
16
3
9
48
256

12
17,4
2
4
34,8
302,76

13
17,2
2
4
34,4
295,84

14
17,4
2
4
34,8
302,76

15
15,7
3
9
47,1
246,49

16
17,1
2
4
34,2
292,41

Σ
232,4
61
299
787,9
3521,52


т.к. n=16, то = = 14,525

= = 3,8125

тогда


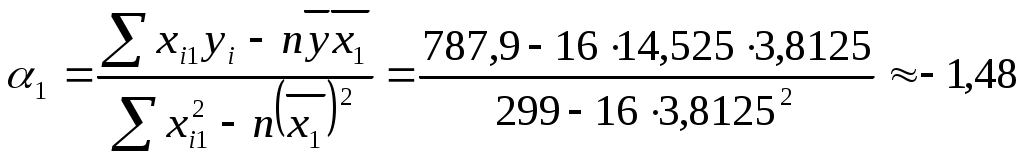
таким образом, получаем уравнение регрессии:

Составим таблицу для = β0+ β1x1: (таблица 3)


i
yi
xi2
xi22
yi xi2
yi2

1
14,4
154
23716
2217,6
207,36

2
16,9
155
24025
2619,5
285,61

3
13
149
22201
1937
169

4
9,6
128
16384
1228,8
92,16

5
9,8
134
17956
1313,2
96,04

6
9,6
127
16129
1219,2
92,16

7
16,8
157
24649
2637,6
282,24

8
14,8
160
25600
2368
219,04

9
9,8
134
17956
1313,2
96,04

10
16,9
154
23716
2602,6
285,61

11
16
161
25921
2576
256

12
17,4
167
27889
2905,8
302,76

13
17,2
163
26569
2803,6
295,84

14
17,4
163
26569
2836,2
302,76

15
15,7
155
24025
2433,5
246,49

16
17,1
162
26244
2770,2
292,41

Σ
232,4
2423
369549
35782
3521,52


т.к. n=16, то = = 14,525

= = 151,4375

тогда


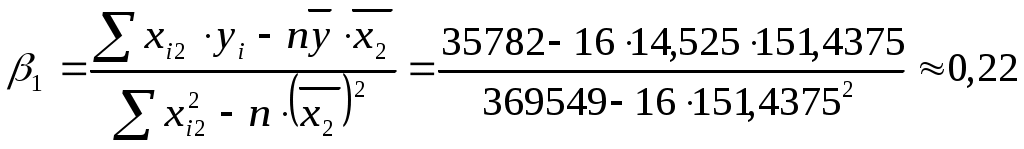
таким образом, получаем уравнение регрессии:

1.3. С помощью коэффициентов парной корреляции проанализировать тесноту линейной связи между ценой и возрастом автомобиля, а также между ценой и мощностью двигателя. Проверить их значимость с надежностью 0,9.

Найдем коэффициент парной корреляции для = α0+ α1x1:



проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем:



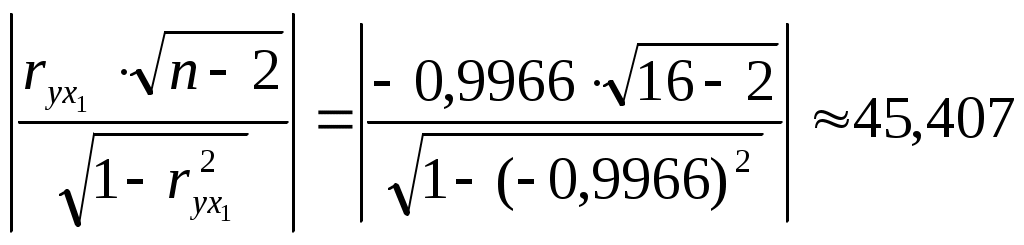
Сравним с квантилем распределения Стьюдента

Т.к. 45,407 >1,761, то коэффициент корреляции существенно отличается от нуля и существует сильная линейная зависимость между y и
Найдем коэффициент парной корреляции для = β0+ β1x2:



проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем:



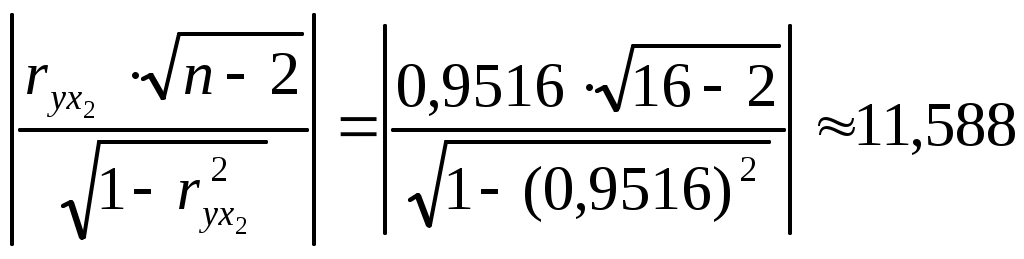
Сравним с квантилем распределения Стьюдента

Т.к. 11,588 >1,761, то коэффициент корреляции существенно отличается от нуля и существует сильная линейная зависимость между y и

1.4. Проверить статистическую значимость параметров и уравнений регрессии с надежностью 0,9.

Для

Коэффициент детерминации: , т.е. вариация цены на 99% объясняется вариацией возраста автомобиля.

Фактическое значение F-статистики Фишера



При уровне значимости 0,1 табличное значение .

Т.к. 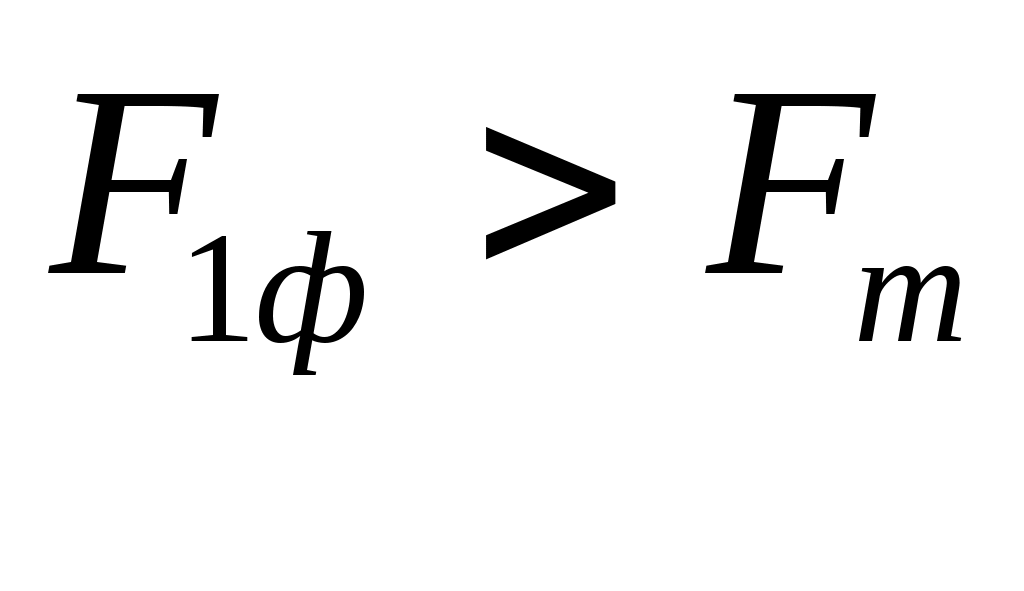, то признается статистическая значимость уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии найдем , признается статистическая значимость коэффициентов регрессии.

Аналогично для :

Коэффициент детерминации: , т.е. вариация цены на 91% объясняется вариацией возраста автомобиля.

Фактическое значение F-статистики Фишера



При уровне значимости 0,1 табличное значение .

Т.к. 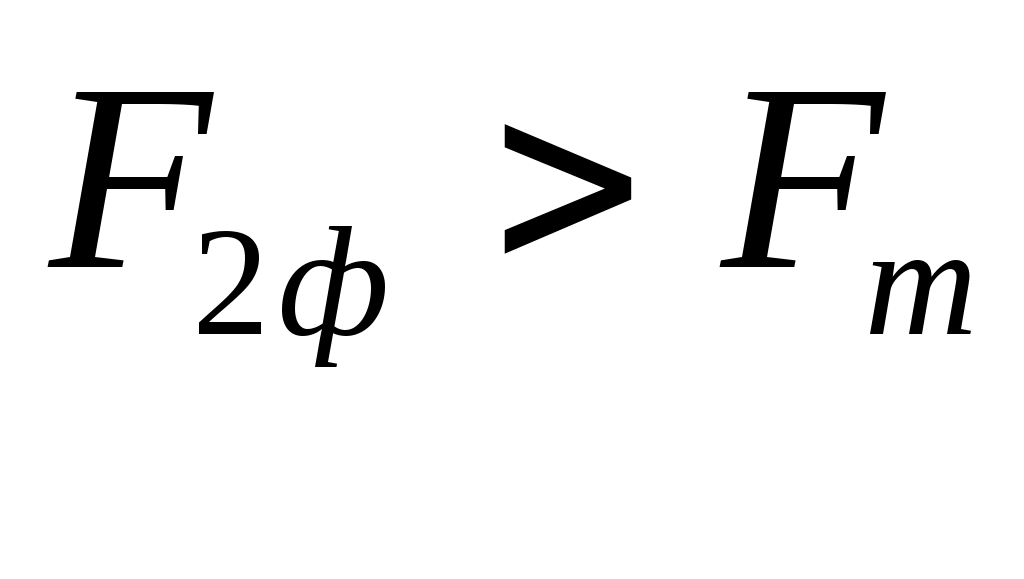, то признается статистическая значимость уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии найдем , признается статистическая значимость коэффициентов регрессии.
1.5. Построить доверительные полосы надежности для среднего значения цены автомобиля в зависимости от его возраста, а также от мощности двигателя. Изобразить графически линии регрессии и доверительные полосы вместе с полями рассеяний.

Найдем доверительную полосу для уравнения регрессии , построим вспомогательную таблицу: (таблица 4)

Смотрите также файлы